非线性规划-外罚函数&内罚函数

外罚函数

其中对于称为惩罚项，M为惩罚因子，p(x)称为惩罚函数（一般k取2）

 对于外罚函数，值得注意的是：1.可以解决同时包含不等式和等式约束的规划问题。2.不等式约束的条件为小于等于，如果符号不同时需要进行转换。

例题分析

根据外罚函数求解：

手写比较方便就直接放图片了，中心思想就是进行分类讨论。 在第二种情况里面少写了几个步骤，在得出时，将x1带回等式一可以求得，由于M是趋近无穷大的数，所以可以得出x1=1/3, x2 = 2/3

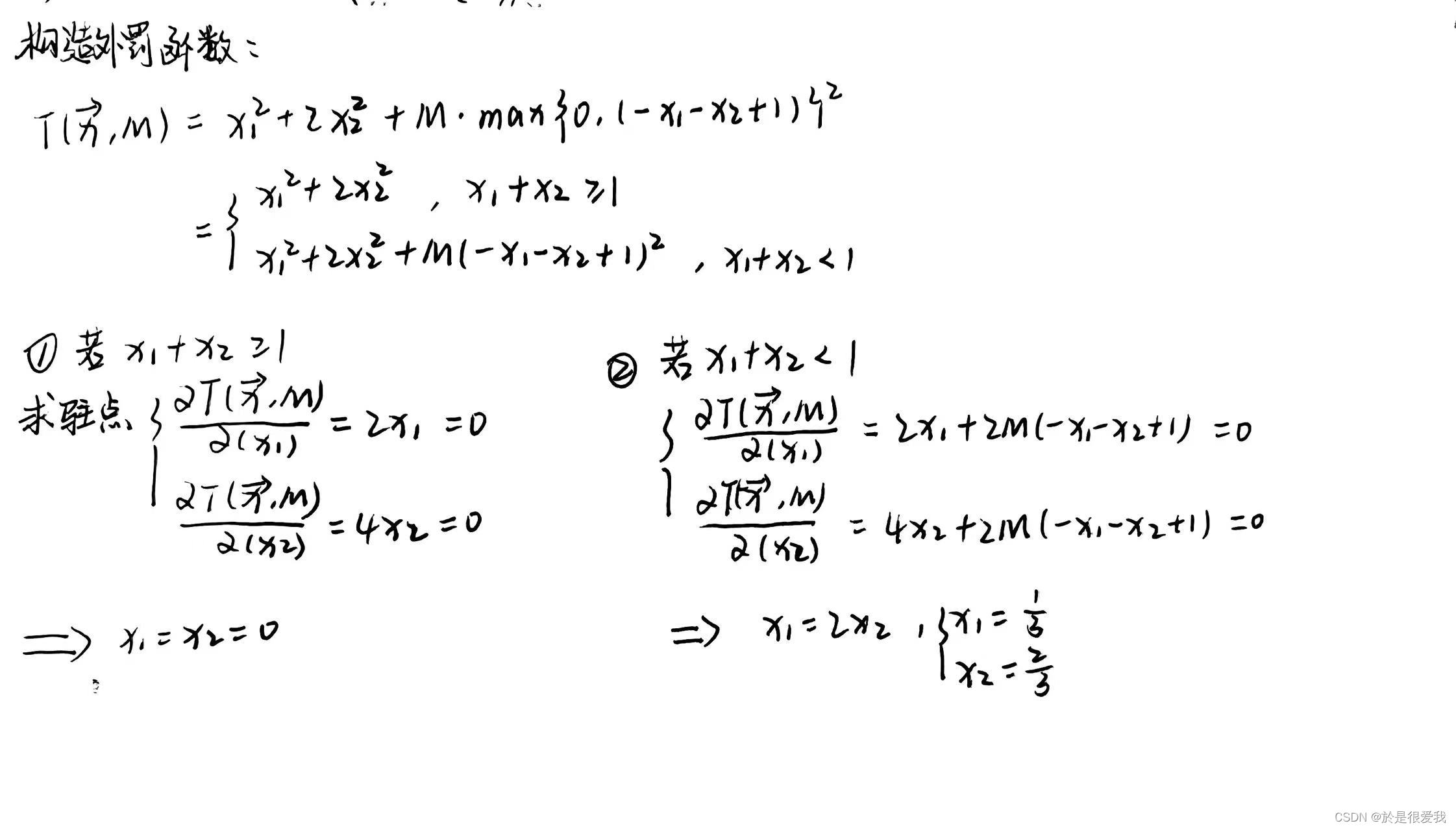
 这个题目比较简单，跟上面也类似

 内罚函数

 注意：内罚函数只能求解包含不等式的约束规划问题，这里的R是趋近无穷小。另外，这里的gi(x)符号为大于等于。在内罚函数中惩罚函数的构造形式也不同，途中给出两种常用的形式：倒数障碍函数和对数障碍函数（注意对数障碍函数前面有负号）。

例题分析