数据挖掘中的几个相似性度量

一.  余弦相似度

余弦相似度的基本概念
余弦相似度是一种衡量两个非零向量之间方向相似性的方法。它通过计算两个向量的夹角的余弦值来评估它们之间的相似性。余弦相似度的值介于-1和1之间，其中1表示两个向量完全相同（方向一致），0表示两个向量正交（方向垂直），而-1表示两个向量完全相反（方向一致但方向相反）。余弦相似度是一个无量纲的指标，它只关注向量的方向，而不受向量长度的影响.

余弦相似度公式

余弦相似度主要使用向量空间中两个向量夹角的余弦值作为相似性度量的指标，主要用于计算文档数据之间的相似性。假设两个文档向量(x1,y1)与(x2，y2)，将其放置在直角坐标系中，其夹角余弦如下所示。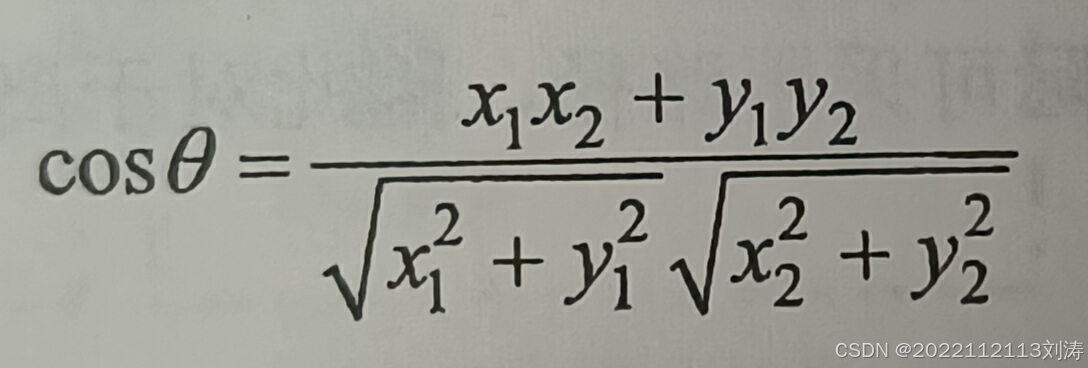

余弦相似度的特点和应用
余弦相似度的一个显著特点是它忽略了向量的长度，这使得它在处理高维数据时表现良好，尤其是在文本分析和推荐系统等领域。此外，余弦相似度的计算基于简单的数学公式，易于编程实现，并且在低维空间中计算速度较快。在实际应用中，余弦相似度通常用于比较文档、关键词提取、情感分析、用户兴趣相似度计算以及物品推荐等.
 

余弦相似度与欧氏距离的对比
与余弦相似度相比，欧氏距离是一种衡量向量之间距离的度量，它考虑了向量的长度和方向。在某些情况下，欧氏距离可能更适合于需要考虑向量长度的应用场景。然而，在高维数据中，由于“维度的诅咒”，欧氏距离可能会受到噪声和无关特征的影响，而余弦相似度则更加稳健.

二.  欧式距离

欧式距离的来源

欧式距离（Euclidean Distance）是一种在多维空间中衡量两点之间直线距离的方法，它的概念最早可以追溯到古希腊数学家欧几里得（Euclid）。在欧几里得几何中，两点之间的距离是通过勾股定理来计算的，而欧式距离正是这一概念在多维空间中的推广。在二维或三维空间中，欧式距离可以直观地表示为两点之间的直线距离，而在更高维的空间中，欧式距离的计算仍然遵循类似的原理，即通过计算两点在各个维度上差值的平方和的平方根来获得。欧式距离的理解欧式距离的计算公式在n维空间中表达为： 分别是向量在第i个维度上的分量。这个公式表明，欧式距离考虑了空间中的所有维度，并且给予了每个维度相同的权重。在实际应用中，欧式距离广泛用于聚类分析、模式识别、数据挖掘等领域，因为它能够反映出多维空间中点之间的实际距离。分别是向量在第i个维度上的分量。

公式

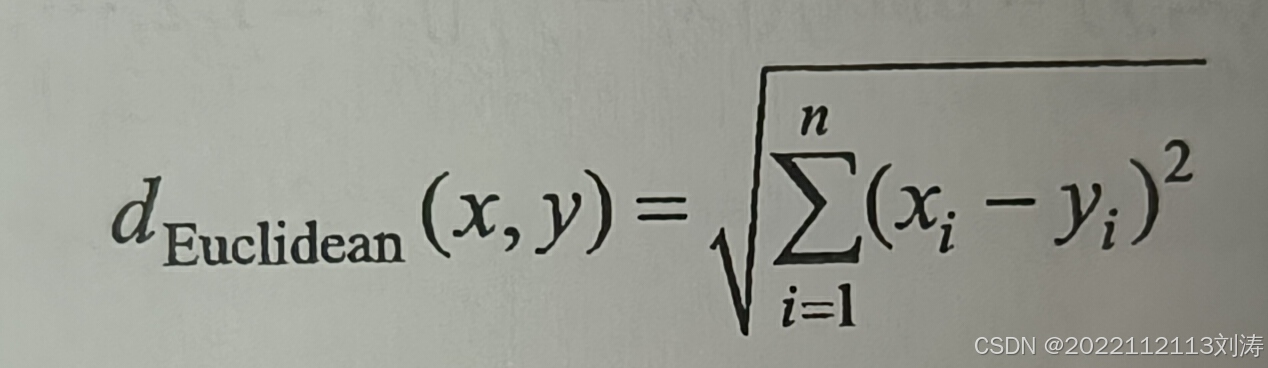
这个公式表明，欧式距离考虑了空间中的所有维度，并且给予了每个维度相同的权重。在实际应用中，欧式距离广泛用于聚类分析、模式识别、数据挖掘等领域，因为它能够反映出多维空间中点之间的实际距离。

注意事项

尽管欧式距离在很多情况下都是一个有用的距离度量，但它也有局限性。例如，欧式距离对尺度敏感，如果数据中某些维度的尺度远大于其他维度，那么这些维度将在距离计算中占据主导作用。此外，欧式距离没有考虑数据的方向性，即它只计算了向量的长度，而忽略了向量方向的差异。在处理这些问题时，可能需要采用标准化欧式距离或其他距离度量方法，如马氏距离，来更准确地描述数据之间的相似性。

三.  马氏距离

马氏距离的来源

马氏距离（Mahalanobis distance）是由印度统计学家P. C. Mahalanobis提出的，它是一种用于衡量多维数据集中点与分布之间距离的统计量。马氏距离考虑了数据的协方差结构，因此能够捕捉变量之间的线性关系，并且是尺度无关的，即独立于测量尺度。

马氏距离的理解
马氏距离的核心在于它不仅仅是衡量点与点之间的距离，而是考虑了整个数据集的协方差结构。在多维数据中，不同特征之间可能存在相关性，这意味着一个特征的变化可能伴随着其他特征的变化。马氏距离通过使用协方差矩阵的逆来调整这些相关性的影响，从而提供了一种更为精确的距离度量。
当协方差矩阵为单位矩阵时，马氏距离简化为欧氏距离，这表明在变量相互独立的情况下，马氏距离与传统的欧氏距离是等价的。如果协方差矩阵是对角矩阵，马氏距离则是正规化的欧氏距离，考虑了变量的尺度差异。在实际应用中，马氏距离可以帮助识别离群点，因为它能够放大那些在协方差矩阵中方差较大的特征方向上的偏差。此外，马氏距离在模式识别、聚类分析和降维技术（如主成分分析PCA）中都有重要应用。 是数据集的协方差矩阵，
其中，马氏距离的计算公式为： 

马氏距离的一个重要特点是它要求协方差矩阵必须是可逆的，这意味着数据集不能有线性相关的特征，或者至少协方差矩阵不能是奇异的。在某些情况下，如果数据集的维度非常高，可能需要先进行降维处理，如PCA，以确保协方差矩阵的稳定性。

四.  曼哈顿距离

曼哈顿距离的来源

曼哈顿距离（Manhattan Distance），也被称作出租车距离或城市街区距离，是一种在几何空间中测量两点之间距离的度量方式。它的名称来源于美国纽约市的曼哈顿区，该区域的街道呈网格状布局，车辆在街道上行驶时通常需要沿直线前进，即只能向东、西、南、北四个方向移动，不能直接沿对角线行驶。因此，两点之间的最短路径是沿着这些垂直和水平的街道，这就是曼哈顿距离的直观表现。曼哈顿距离的数学表达和理解 可以通过以下公式计算：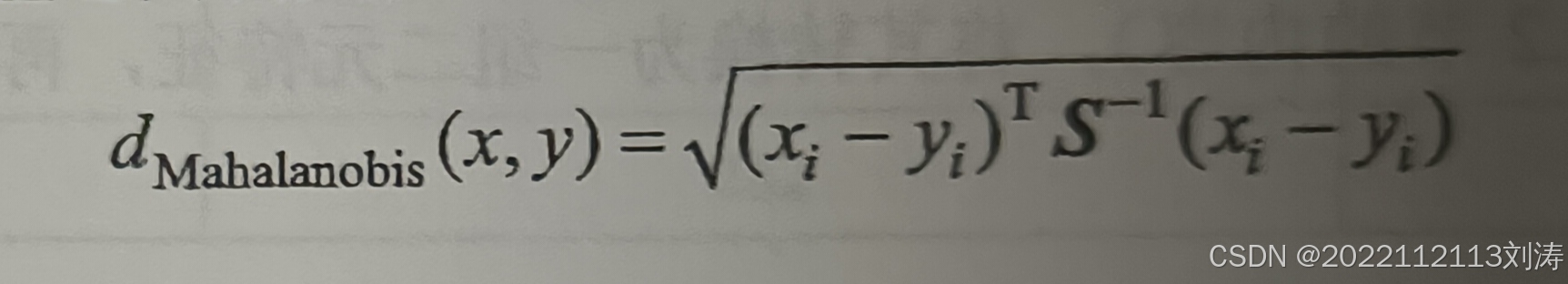

在数学上，曼哈顿距离可以定义为两点在标准坐标系上的绝对轴距之总和。在二维平面上，如果有两个点 ，它们之间的曼哈顿距离  和 这个公式表示的是两点在 X 轴和 Y 轴方向上的坐标差值的绝对值之和。在更高维度的空间中，曼哈顿距离的计算方式类似，只是涉及到更多的坐标轴。

曼哈顿距离的特性

曼哈顿距离具有以下几个重要的数学性质：非负性：两点之间的距离是非负的。同一性：一个点到自身的距离为零。对称性：两点之间的距离与起点和终点的顺序无关。三角不等式：从一点到另一点的距离小于或等于通过第三点的路径长度。此外，曼哈顿距离依赖于坐标系统的取向，当坐标轴发生旋转时，点间的距离会变化。这与欧氏距离不同，后者是独立于坐标系取向的。曼哈顿距离的应用曼哈顿距离不仅在现实世界的导航和路径规划中有实际应用，如在曼哈顿岛上驾车，还在计算机科学、图像处理、数据挖掘等领域中广泛使用。例如，在棋类游戏中，某些棋子的移动距离可以用曼哈顿距离来计算；在机器学习中，曼哈顿距离可以用来衡量样本之间的相似性或在聚类分析中作为距离度量。