【编译原理】题目合集（二）

未经许可，禁止转载。

判断题

（1）一个上下文无关文法的开始符号可以是终结符或非终结符。（错，只能是非终结符）
（2）对于文法，句子是仅含终结符号的句型。（对）
（3）一棵分析树是不同推导过程的共性抽象。（对）
（4）一个文法是二义的，则这个文法的每个句子都对应两个不同的语法树。（错，举个例子：S->a|SS，这个文法是二义的，但句子a只对应一棵语法树。）
（5）上下文无关文法的描述能力和有限自动机相同。（错，有限自动机描述能力与正则表达式一致，但小于上下文无关文法的描述能力。）

思政问答

唯物辩证法中有三条基本规律，即对立统一规律、质量互变规律和否定之否定规律。使用唯物辩证法对编译程序（C）和解释程序（Python）进行剖析。

解：
编译程序执行效率高、错误检查方便，但开发迭代慢、灵活性差；解释程序可快速迭代、灵活性高，但错误检查能力有限，同时解释器直接读取并执行源代码，因此可能存在安全风险。矛盾着的双方既对立又统一，从而推动着事物的发展，可以将二者结合，提高效率。

构造文法(1)

对如下语言构造相应的文法

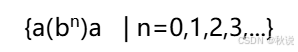
解，构造G[S]如下：
S->aAa
A->bA|空

构造文法(2)

对如下语言构造相应的文法

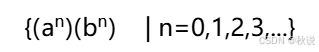
解，构造G[S]如下：
A->aAb|空

写出语言对应的句子

由A=>CB=>C CB、A=>BA=>B BA、A=>BA=>CB A，共得到 aab, abb, bab, bbb, aba, bba 共6个句子。

证明文法二义(1)

解：
判断一个文法二义，可以采用以下三种方法之一：
1.给出一个串，说明可以为其构造两棵不同的分析树。
2.给出一个串，说明可以为其构造两个不同的最左推导。
3.给出一个串，说明可以为其构造两个不同的最右推导。
说明：如果对于一个串构造一个最左推导和一个最右推导，则不可证明文法二义。
（1）对于输入0*1-2可构建出两棵不同的分析树，因此本文法二义，如图所示：

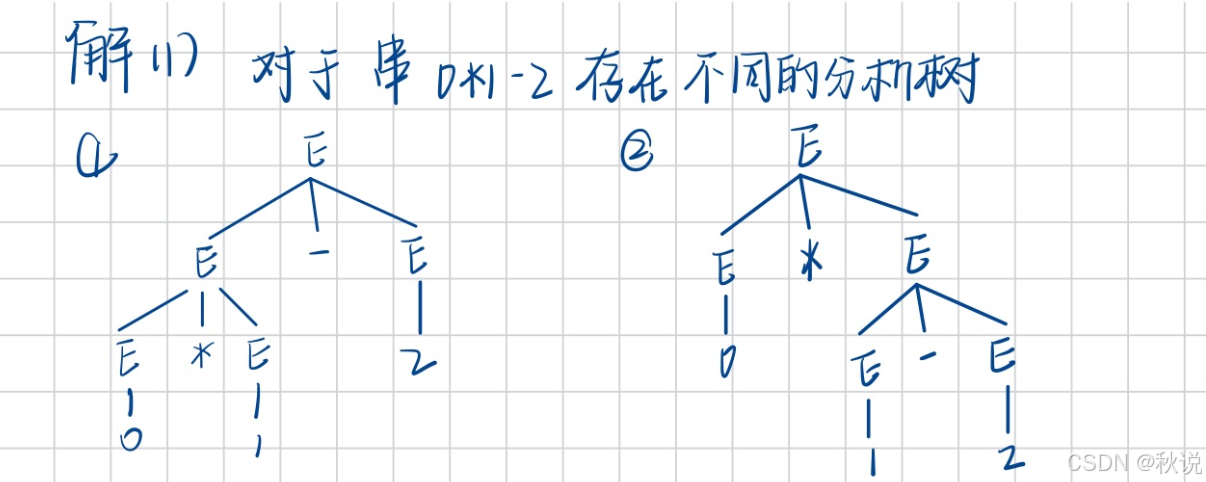
（2）可构造5课分析树

(1*2)-(3*4)
((1*2)-3)*4
1*(2-(3*4))
(1*(2-3))*4
1*((2-3)*4)

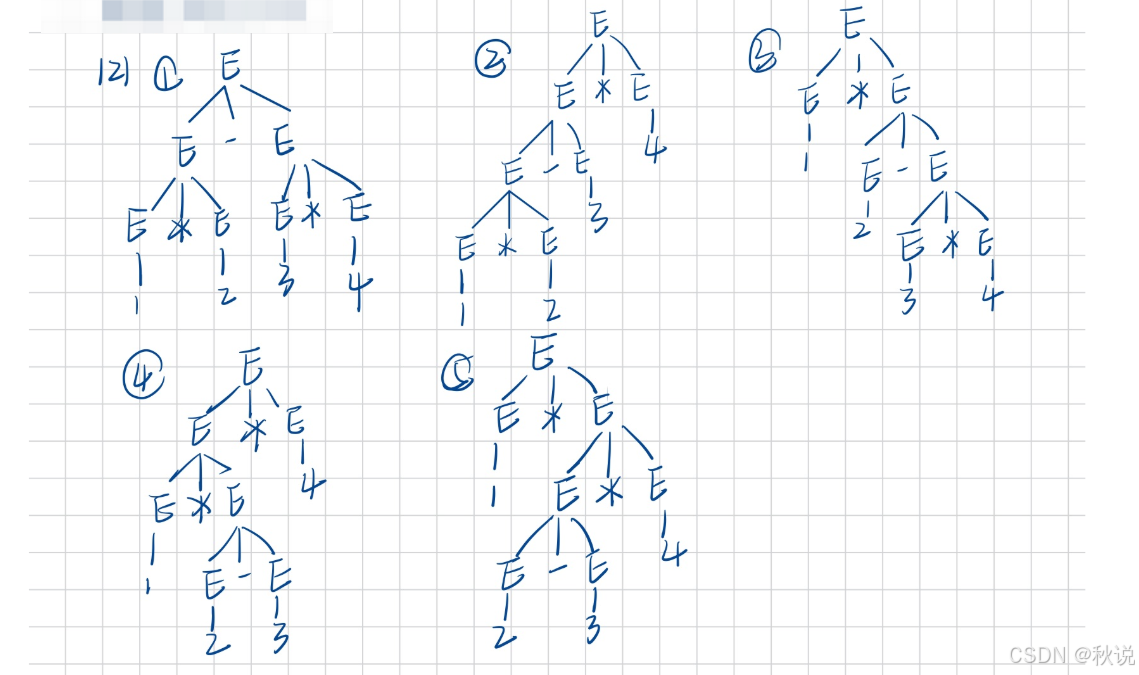
证明文法二义(2)

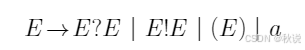
证明该文法是二义文法

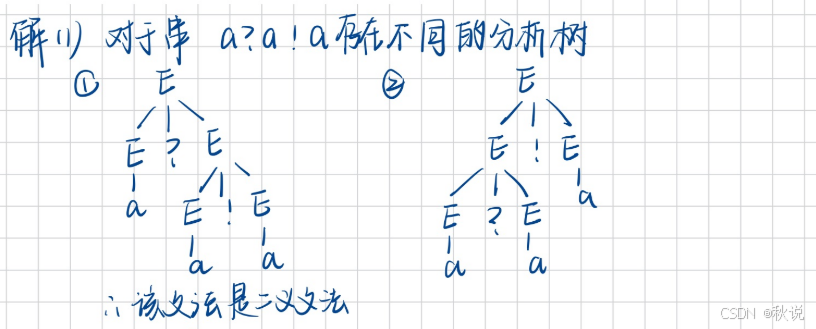
证明文法二义(3)

构造注释分析树

解（1）构造分析树，输入串是1011，根据所给文法，构造的分析树如下所示：

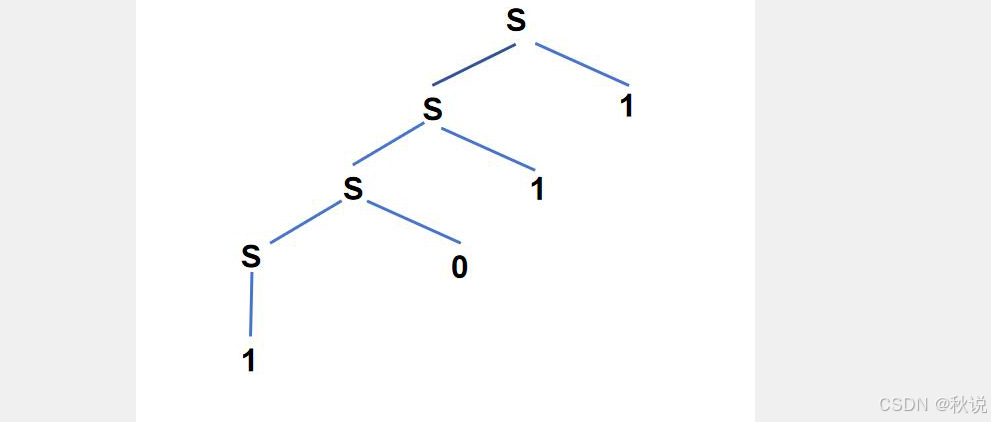
（2）注释分析树
第一步：标记属性。题目只有一个非终结符S，S只有一个属性t，所以标记属性的结果是：

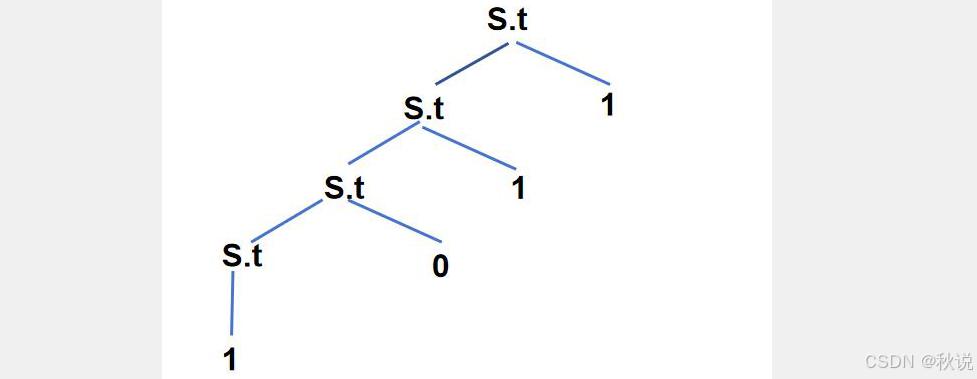
第二步：计算属性值；属性t是综合属性，自下而上计算即可。
对于最底层，对应文法规则和语义规则是：

则属性值计算结果是：

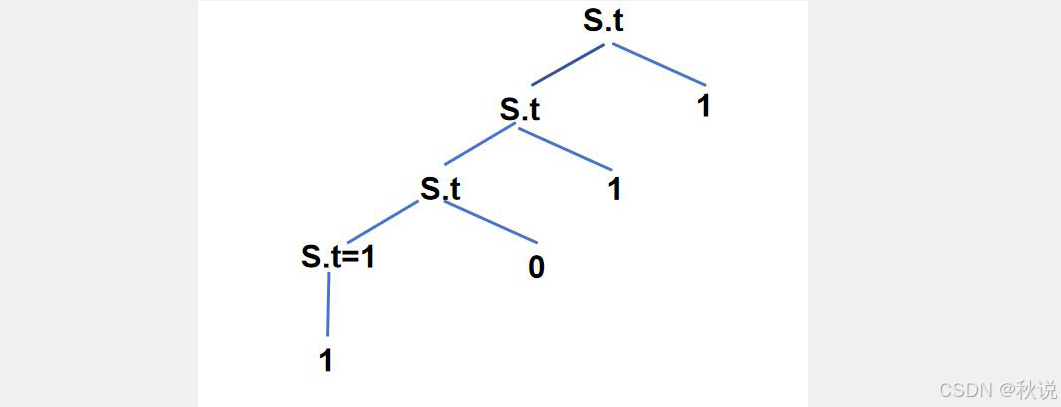
对于第三层，对应文法规则和语义规则是：

则属性值计算结果是：

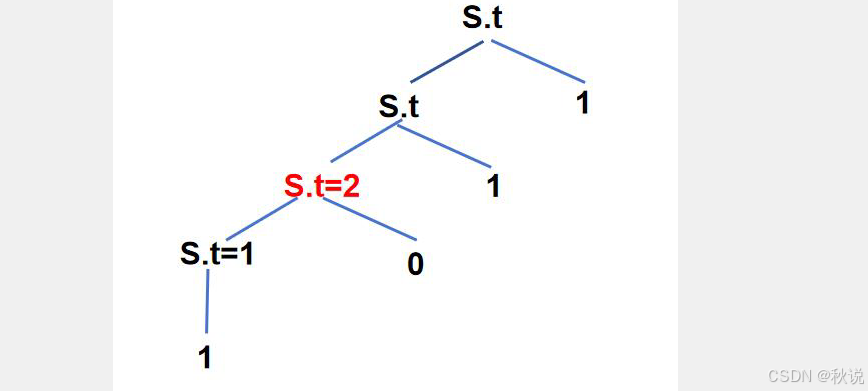
对于第二层，对应文法规则和语义规则是：

则属性值计算结果是：

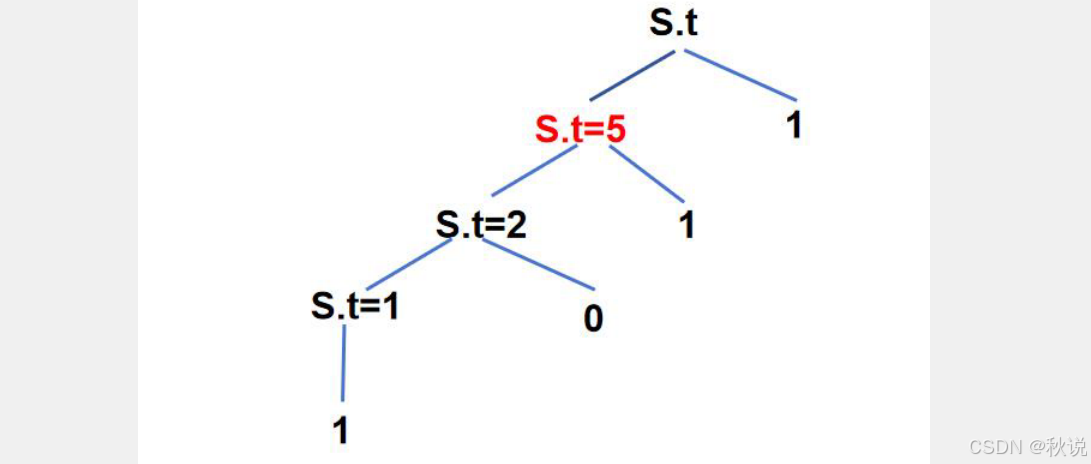
对于第一层，对应文法规则和语义规则是：

则属性值计算结果是：

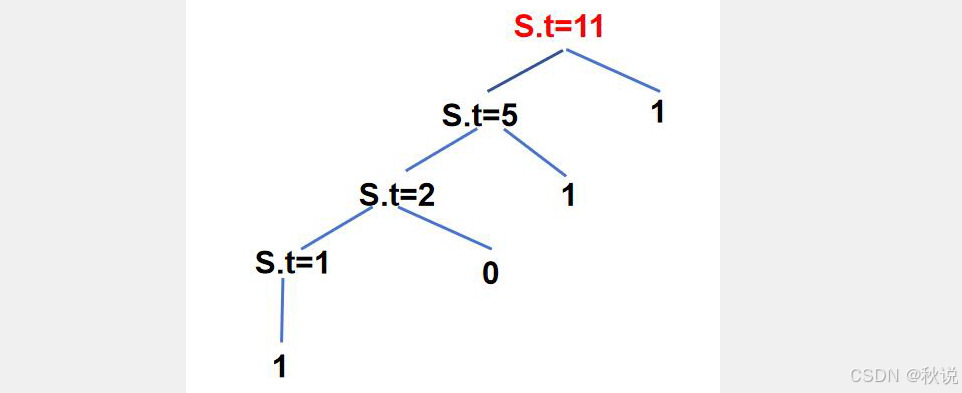
句型个数判断(1)

以下文法会产生多少个不同的句型？
A->BB B->CC C->1 | 2
解：
1.没有长度为0的串
2.长度为1的串有一个A
3.长度为2的串有一个BB
3.长度为3的串：
A=>B B=>B CC，即B开头，后面两个分别可能为C或1或2，一共3x3=9个
A=>B B=>CC B，即B结尾，前面两个分别可能为C或1或2，一共3x3=9个
共18个
4.长度为4的串：A=>BB=>CCB=>CCCC，C可以取C或1或2，一共有3x3x3x3=81个
所以总句型数为：1+1+9+9+81=101个

句型个数判断(2)

以下文法会产生多少个不同的句型
A->BB B->CC C->1|2|ε
解：
1.长度为0的串：A=>BB=>BCC=>CCCC ，将C全部替换为空串ε，因此长度为0的串有1个
2.长度为1的串
A为长度为1的串
A=>BB=>BCC，将C全部替换为空串，剩下串B
A=>BB=>CCCC，将任意3个C替换为空串，剩下C，即A=>C，其中C可以是C或1或2，因此这里有3个
共5个
3.长度为2的串
A=>BB，B=>CC，C=>1|2
所以长度为2的串为：BB, BC, B1, B2, CB, CC, C1, C2, 1B, 1C, 11, 12, 2B, 2C, 21, 22
共16个
4.长度为3的串
A=>BB=>BCC，C可以是C或1或2，则B开头的长度为3的句型共有9个
A=>BB=>CCB，C可以是C或1或2，则B结尾的长度为3的句型共有9个
A=>BB=>CCB=>CCCC=>CCC，C可以是C或1或2，则此处长度为3的句型共有3x3x3个
共45个
5.长度为4的串
A=>BB=>CCCC，C可以是C或1或2，则此处长度为4的句型共有3x3x3x3=81个
所以句型总数为：1+5+16+45+81=148个

写出正则表达式(1)

写出以下定义在字母表{0，1}之上的正则表达式。
以1结尾，并且不含子串00的串。
解：(1|01)+
注意：(1|01)*1不能表示0101，因此不符合。

写出正则表达式(2)

写出以下定义在字母表{0，1}之上的正则表达式。
以偶数个0开头，后接奇数个1的串。
解：(00)*1(11)*
注意：(00)*表示0个00或多个00，0个00也算偶数个0。

写出正则表达式(3)

写出以下定义在字母表{0，1}之上的正则表达式。
开头和结尾符号不一样的串。
解：首符号与尾符号不同，共有两种情形：
1.首符号为0，尾符号为1
2.首符号为1，尾符号为0。
3.将这两种情形分别用正则式表示，再进行或运算即可。
(0(0|1)*1) | (1(0|1)*0)

写出正则表达式(4)

写出以下定义在字母表{0，1}之上的正则表达式。
不以01结尾的串。
解：所有长度小于2的串，都不会以01结尾；长度大于2的串，结尾有3种情形，以00结尾，以11结尾，以10结尾。
长度为0的串：ε
长度为1的串：0 | 1
长度大于2且不以01结尾的串：(0|1)*(00|11|10)
综上：ε | 0 | 1 | (0|1)*(00|11|10)

写出词法分析器的输出

输入串为：aabbaaabbbaaaabbbb
转化规则如下，给出词法分析器的输出：
ab? {printf(“1%s\n”, yytext);}
a?b(+) {printf(“2%s\n”, yytext );}
a(+)b? {printf(“3%s\n”, yytext );}
aba {printf(“4%s\n”, yytext );}
解：
若匹配到转化规则左边的模式，则执行右边的操作。例如匹配到ab?时，输出1，并紧跟着输出匹配的词素yytext，最后换行。
若同时匹配到多个规则，选取最长匹配的规则，若规则匹配长度相同，则选择最前面的规则进行转化，例如匹配规则2和3，则选取规则2。
1.开头为a，因此考虑ab?、a(+)b?和a*ba*，但只有a(+)b?最长且优先级最高，因此输出3aab
2.经过第一步，删去aab后，剩下baaabbbaaaabbbb
3.可知规则a*ba*最符合，输出4baaa
4.经过第二步，删去baaa后，剩下bbbaaaabbbb
5.可知规则可知规则a?b+最符合，输出2bbb
6.经过第三步，删去bbb后，剩下aaaabbbb
7.可知规则a(+)b?最符合，输出3aaaab
8.经过第三步，删去aaaab后，剩下bbb
9.可知规则a?b(+)最符合，输出2bbb
综上，输出3aab\n 4baaa\n 2bbb\n 3aaaab\n 2bbb\n

写出状态转换图

手工方法给出识别以下正则式所描述语言的状态转换图
b?a(+)b*
解：
（1）将该扩展表示法进行转化，得到

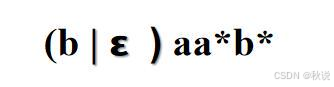
（2）ab为连续闭包，因此需要继续调整，插入一个空：

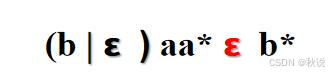
（3）忽略以上两个闭包a和b，画出其余部分对应的状态转换图，注意初态和终态要标记，空边要注明：

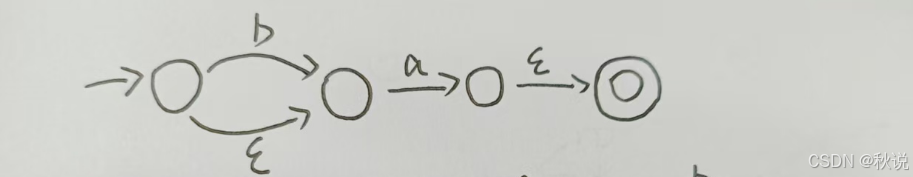
（4）接着画两个闭包，并对状态编号：

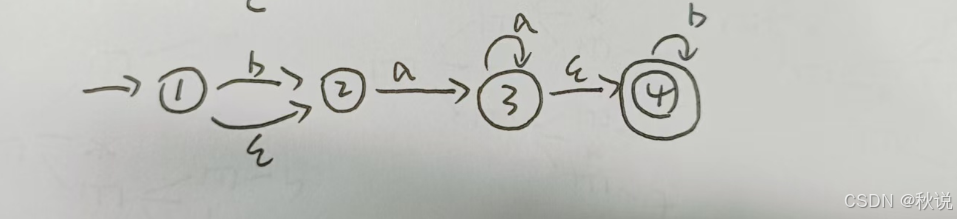
写出状态转换表及DFA

构建以下NFA对应的DFA，给出状态转换表和状态转换图。

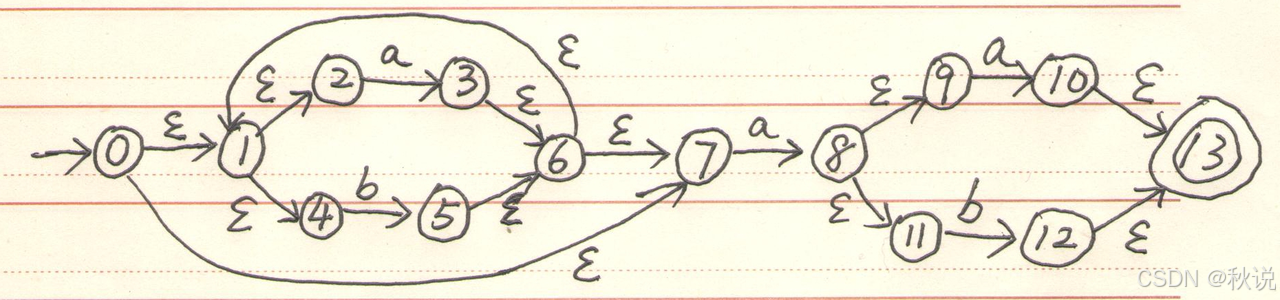
1.先归纳出与a相关的推导、与b相关的推导

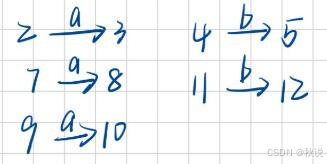
2.对于初态0，可以通过ε推得1、2、4、7，因此表格可写为：

3.对于当前状态集合{1，2，4，7}，输入a时，2将推至3，7将推至8；则新的状态集合以{3，8}开始，同时3和8可以通过ε推得的结果，因此表格可写为：

不断扩展状态转换表，直到没有新状态加入。
由题目可知，NFA的终态为13，因此寻找最终集合中包含13的DFA，即D与E；将D与E加上后缀*

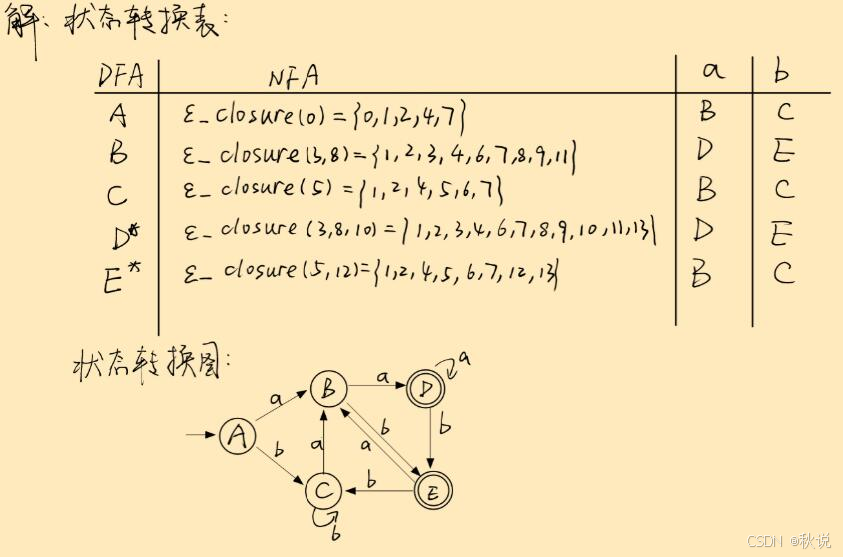
5.画状态转换图（注意标记初态和终态）

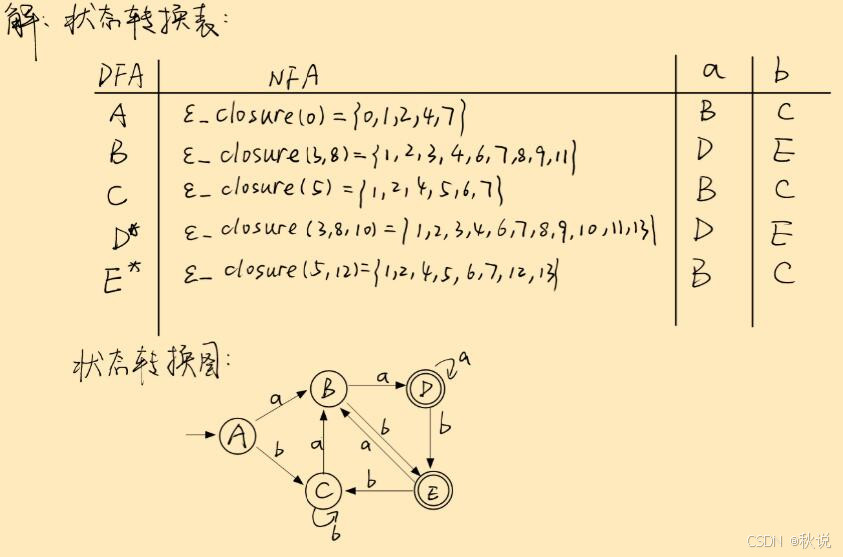
手工法写出NFA并将其最小化(1)

采用手工法将以下正则式转换成NFA，并将所得NFA确定化，然后最小化所得DFA。

解：
1.对拓展表示法进行转化
将(a|b)+转为(a|b)(a|b)*
最终得到(a|b)(a|b)*a(a|b)
2.不考虑闭包(a|b)*
画出：

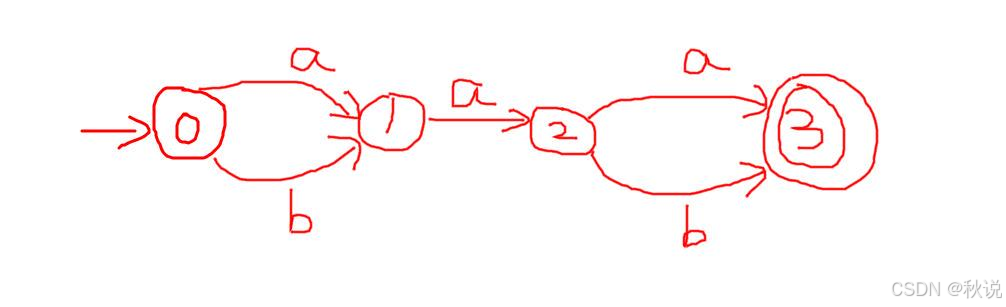
3.加入闭包，得到NFA

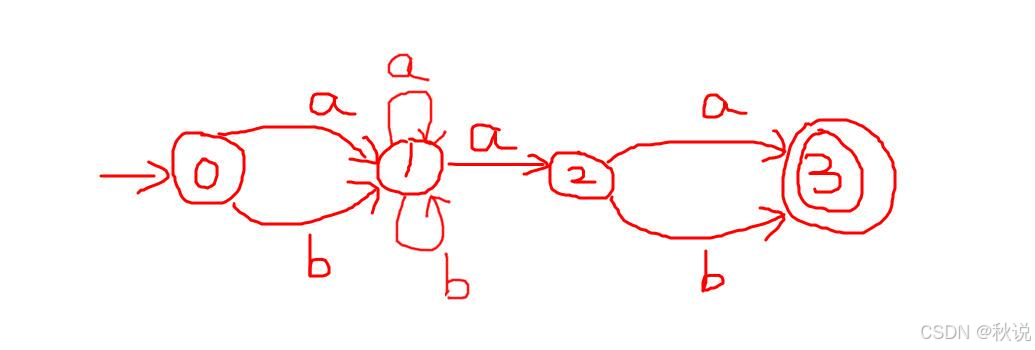
4.归纳出与a相关的推导、与b相关的推导
5.画出状态转换表（NFA的终态为3，因此寻找最终集合中包含3的DFA，即D与E；将D与E加上后缀*）

6.画出DFA，注意：在NFA中，3为终态，因此需要寻找含3的状态集合，即D与E为终态。

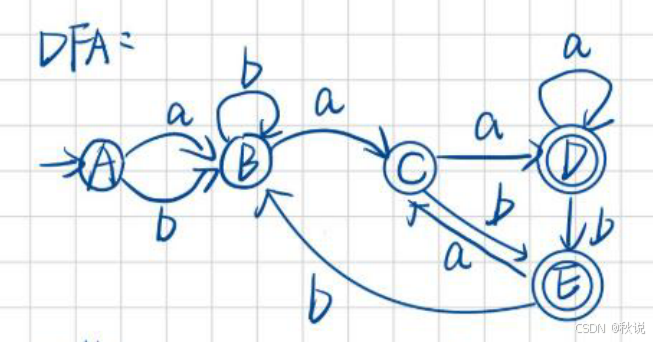
7.接下来要求最小化的DFA。由于D、E为终态，因此可将状态集划分为g1={A B C}和g2={D E}
对于A B C，推a后分别得到B C D，因此A B C不可合并。
对于D E，推a后分别得到D C，因此D E不可合并。
8.无等价状态，该图无需改变，已是最小DFA。

手工法写出NFA并将其最小化(2)

将以下正则表达式转换成NFA和DFA，并最小化。

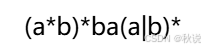
解：
手工法，首先忽略闭包，先画b和a：

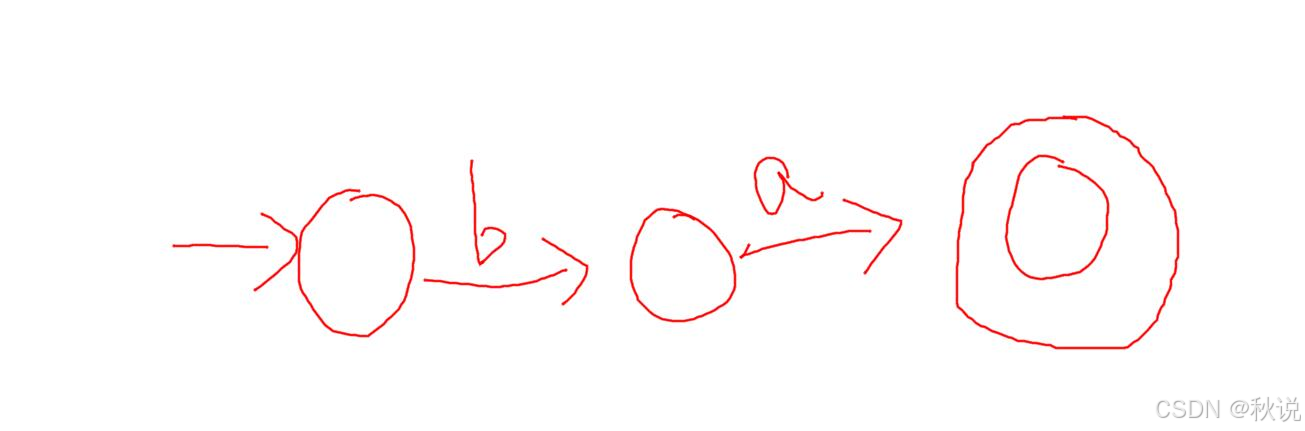
再补上两个闭包，得到：

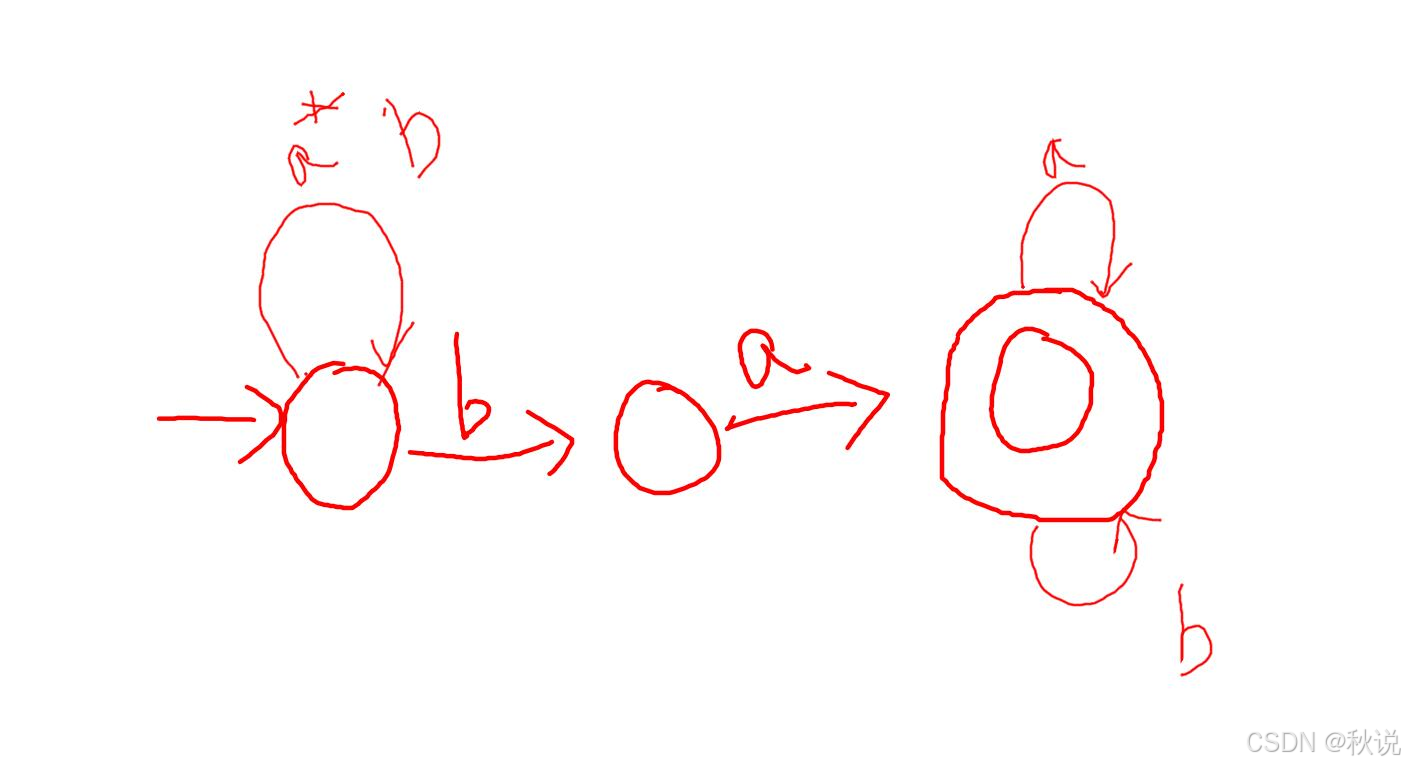
接下来是ab，为了能画a，必须引入一个新的状态，在新的状态上转圈画a，最后的结果：

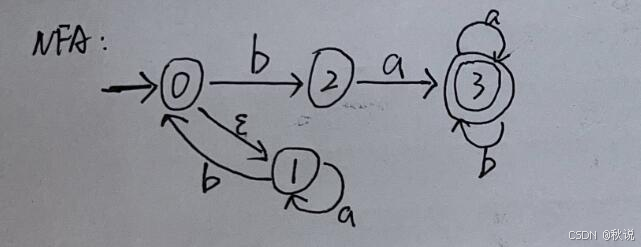
接着构造表格与DFA：

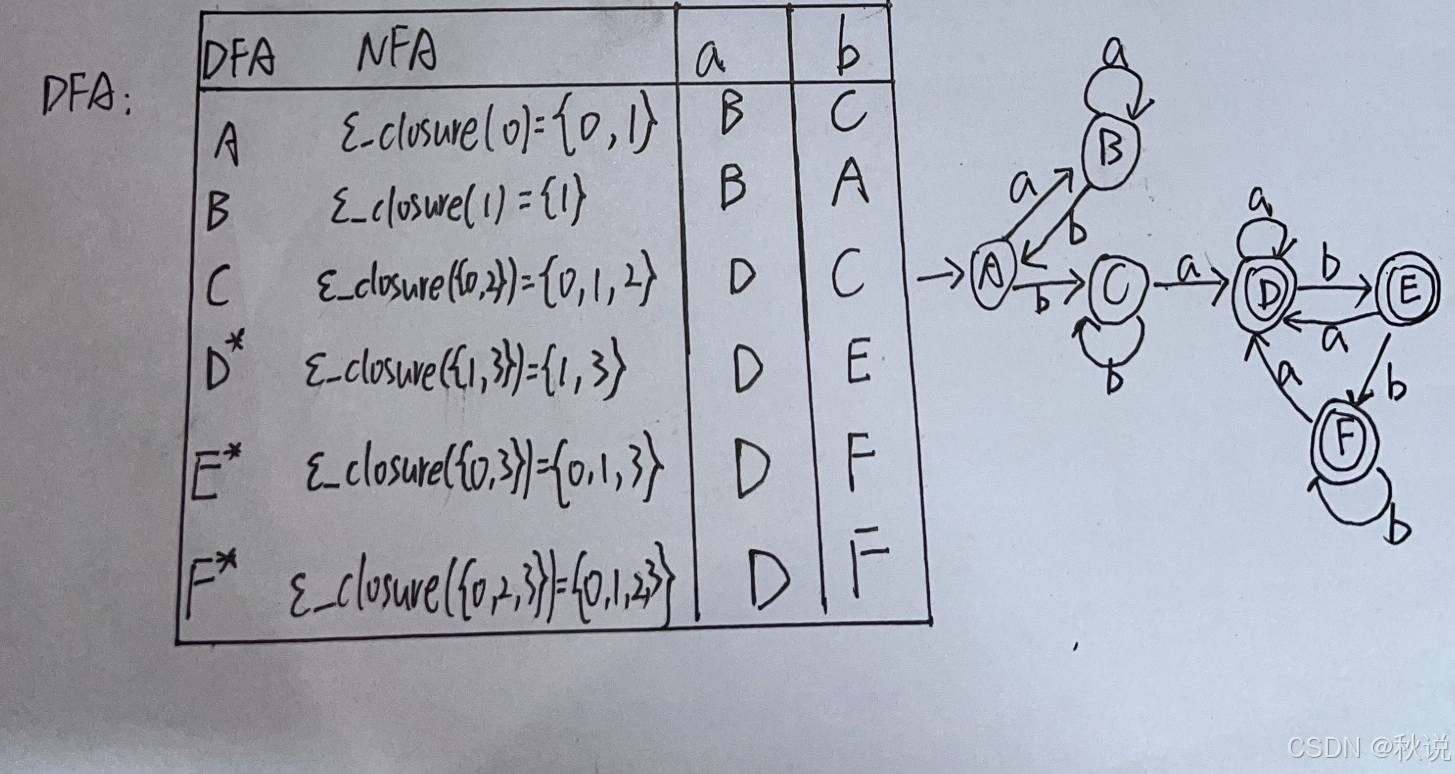
最小化DFA：

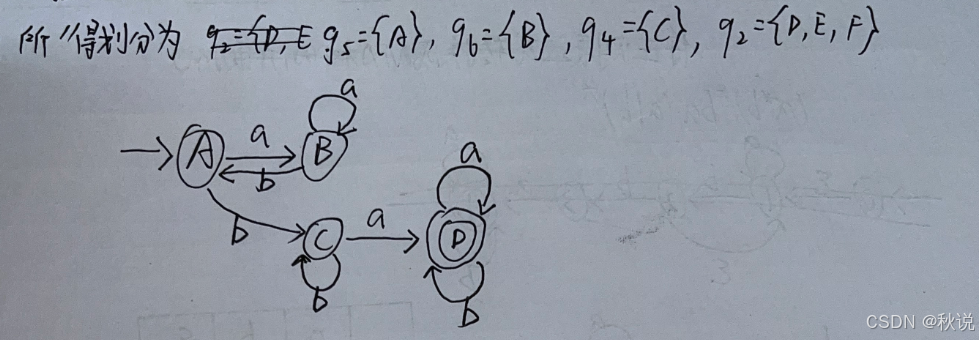
MYT算法写出NFA并将其最小化

采用MYT算法将以下正则式转换成NFA，并将所得NFA确定化，然后最小化所得DFA。

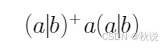
1.对拓展表示法进行转化
将(a|b)+a(a|b)转化为(a|b)(a|b)*a(a|b)
2.使用MYT算法构建NFA

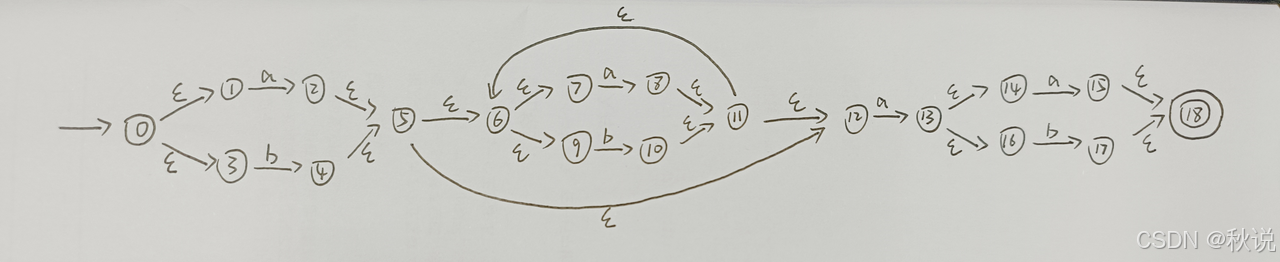
3.画出状态转换表

4.画出DFA

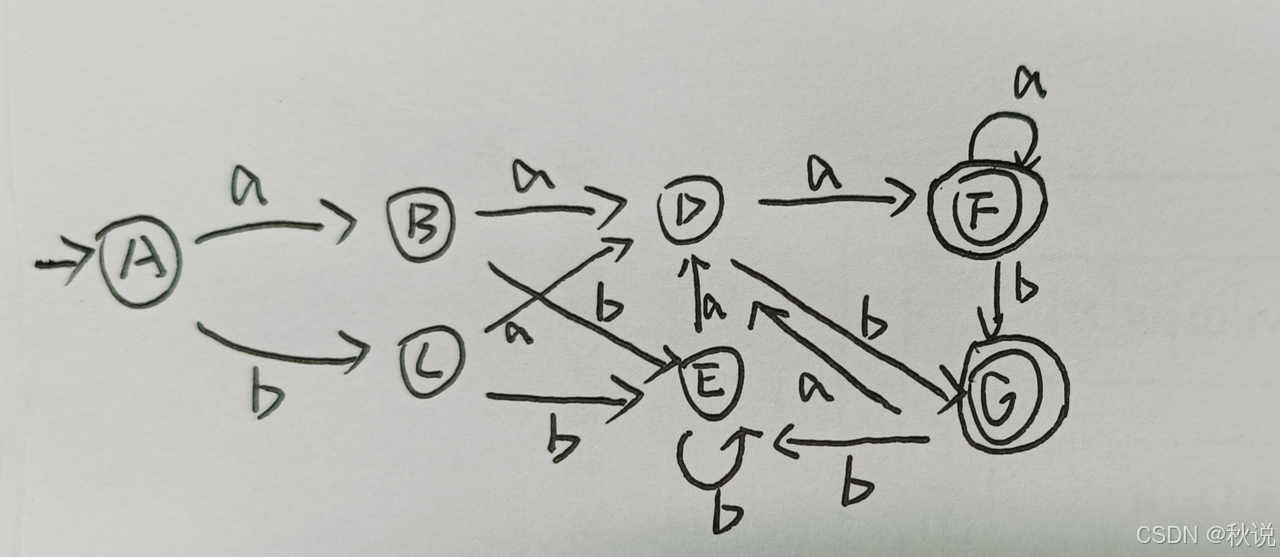
5.找出等价类
A B C D E F G中，G为终态，因此划分为{A B C D E}和{F G}
A经过a到B A经过b到C
B经过a到D B经过b到E
C经过a到D C经过b到E
E经过a到D E经过b到E
D经过a到F D经过b到G
因此等价类可划分为：{A}{B C E}{D}{F G}
F经过a到F F经过b到G
G经过a到D G经过b到E
二者非等价类
因此最终等价类为：{A}{B C E}{D}{F G}
6.最小化DFA的结果如下所示：

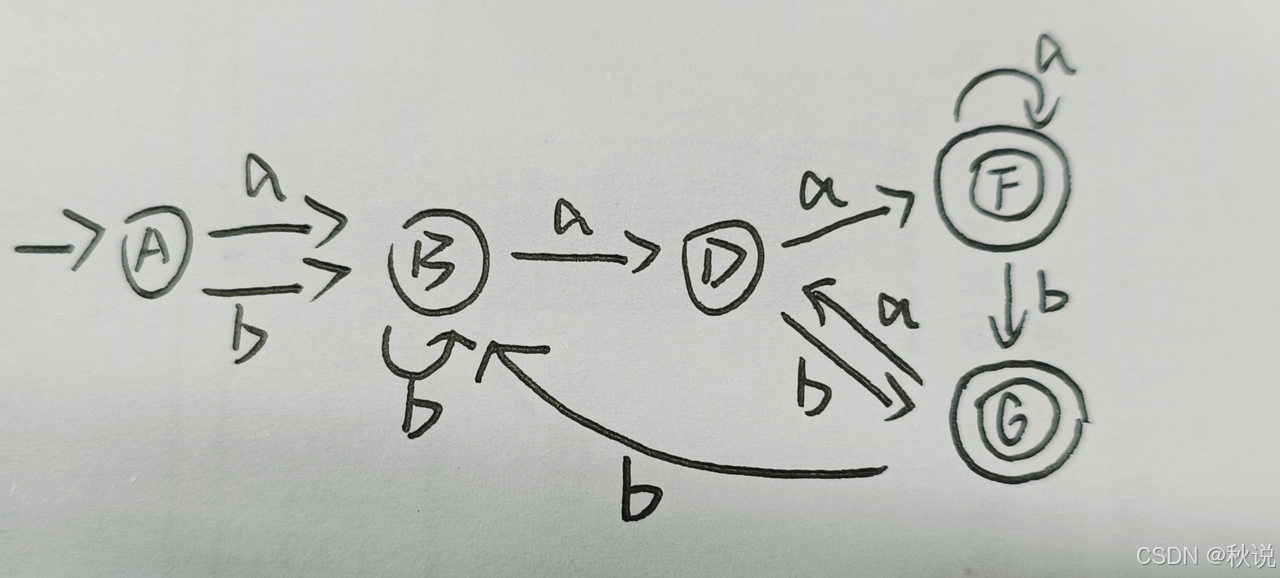
构建多模式词素DFA并将其确定化

给出识别a(a|b)*、b+a?、ba*ba的NFA，并将其确定化。
解：
本题是构建一个识别多个模式词素的DFA。
1.首先为每个模式（正则式）分别构建相应的NFA
2.接下来把它们集成，得到一个统一的NFA。具体操作是：引入一个新的初态，新初态通过空边连向原来各个NFA的初态。
3.接下来将该NFA确定化，由于此时NFA的各个终态的含义不一样，所以确定化时，不仅要说明哪些是终态，更要说明该终态识别的是什么模式。

消除左递归

试消除本文法的左递归
E->E+T|T
T->T*F|F
F->(E)|id
注：第一步设定非终结符顺序；加工文法后，最后需答“所得文法为：”
答：
1.设定非终结符顺序为E T F
2.由于E直接左递归，则引入E’
消除左递归：E->TE’ E’->+TE’ | ε
3.由于T直接左递归，则引入T’
消除左递归：T->FT’ T’->*FT’ | ε
4.所得文法为：
E->TE’ E’->+TE’ | ε
T->FT’ T’->*FT’ | ε
F->(E)|id

求FIRST、FOLLOW、SELECT集

给出此文法每个非终结符的FIRST集和FOLLOW集，给出每条规则的SELECT集。

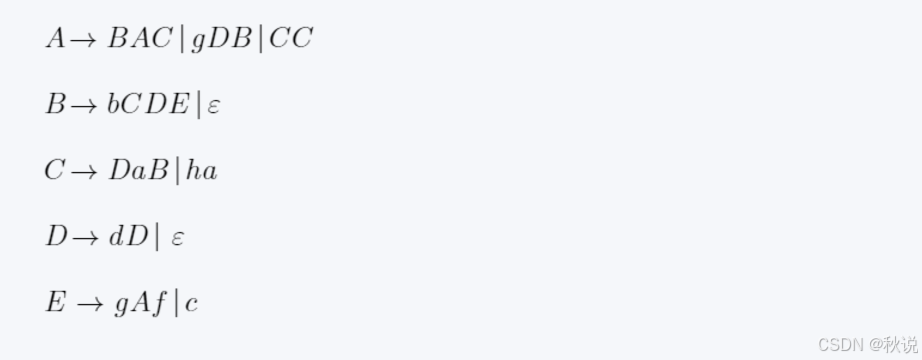
解：
g b a h d f c为终结符
A B C D E 为非终结符
1.判断非终结符的可空性
B可空，因为它有空规则（B->ε）
C的两个产生式均包含终结符，不可空。
D可空，因为它有空规则（D->ε）
E的两个产生式均包含终结符，不可空。
由于C不可空，则A的每个产生式均包含终结符，因此A不可空。
综上所述，B、D可空，A、C、E不可空。
2.求FIRST集

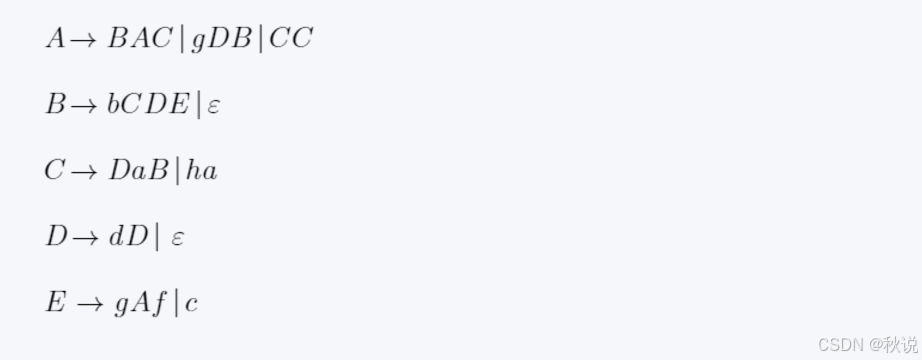
计算A的FIRST集时，则寻找A在箭头左边的表达式。
可以发现是A->BAC|gDB|CC
所以A的FIRST集是BAC、gDB、CC的FIRST集的并集
对于FIRST(BAC)，B可空，因此FIRST(BAC)=(FIRST(B)-{ε}) U FIRST(AC)，由于A不可空，因此化为(FIRST(B)-{ε}) U FIRST(A)
对于FIRST(CC)，由于C不可空，因此化为FIRST(C )
对于FIRST(ha)，由于h不可空，因此化为{h}

3.求FOLLOW集

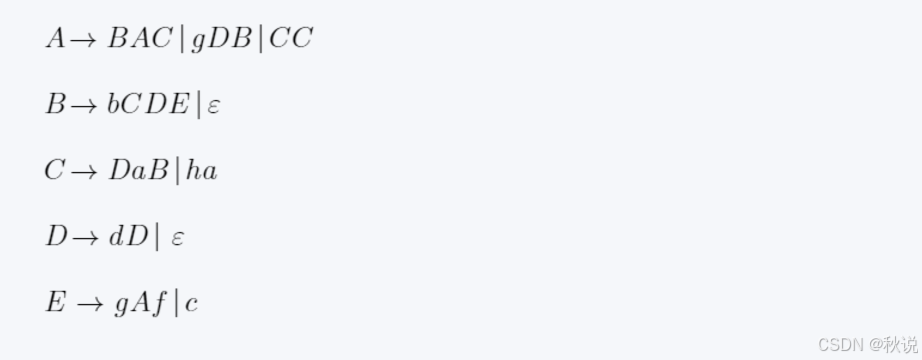
计算A的FOLLOW集时，则寻找A在箭头右边的表达式：

然后找A后边的FIRST集：
对于A->BAC，C不可空，所以得到FIRST(C )；如果C可空，则得到(FIRST©-{ε}) U FOLLOW(A)
对于E->Af,得到{f}
由于A是文法的开始符，所以还有{$}
最终即可得到A的FOLLOW集。

对于FOLLOW(B)，则寻找B在箭头右边的表达式：
A->BAC，得到FIRST(A)
A->gDB，B在最后，所以FOLLOW箭头前的元素，即FOLLOW(A)
C->DaB，B在最后，所以FOLLOW箭头前的元素，即FOLLOW(C )

再看FOLLOW(C )，则寻找C在箭头右边的表达式：
A->BAC，得到FOLLOW(A)
A->CC，这里有两个C，对于前面的C，由于紧跟着的符号是C，且C不可空，所以得到FIRST(C )；对于后面的个C，得到FOLLOW(A)
B->bCDE，因为D可空，E不可空，所以FIRST(DE)=(FIRST(D)-{ε}) U FIRST(E)
最终即可得到C的FOLLOW集。

4.求SELECT集

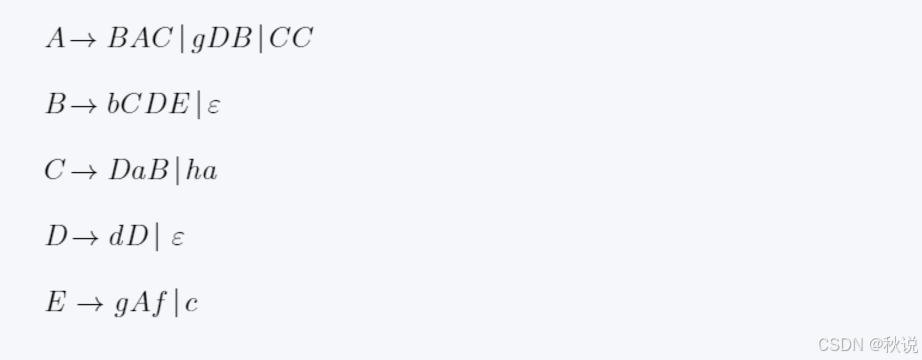
当规则的右部不会导出空时，规则的SELECT集是箭头右部的FIRST集；当规则的右部导出空时，规则的SELECT集是箭头右部的FIRST集减去空，再加上右边的FIRST集或箭头左边的FOLLOW集。
例如：SELECT(A->BAC) 这里B可空，A不可空，所以：

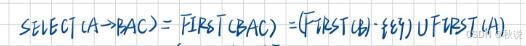
求LL(1)预测分析表并分析输入(1)

现有以下文法：

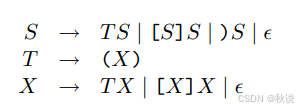
（1）尝试构建LL(1)分析表
解：
LL分析表的行是非终结符，列是终结符+结束标志$。
以S为箭头左部的规则就加入S那一行，以X为左部的规则就加入X那一行；比如说S->TS，箭头左部为S，则加入S那一行。至于加到S那行的哪列，要看箭头右部；比如说S->TS，FIRST(TS)=FIRST(T)={(}，所以得到的是(，因此将S->TS填入第一列。

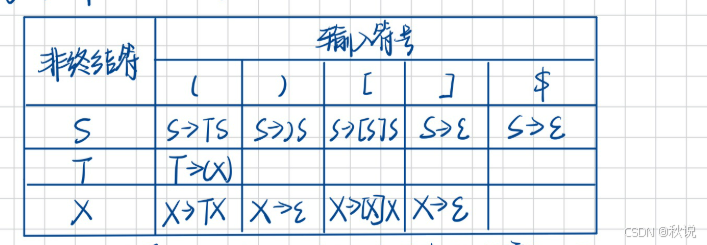
（2）试构建包括错误处理的LL(1)分析表
看每一行的非终结符的FOLLOW集对应的列有没有空白，如果有则说明出错，则在这些空白处填上同步符号synch
比如说对于T行，T的FOLLOW集中对应的) [ ] $列都为空白，则在空白处填上synch

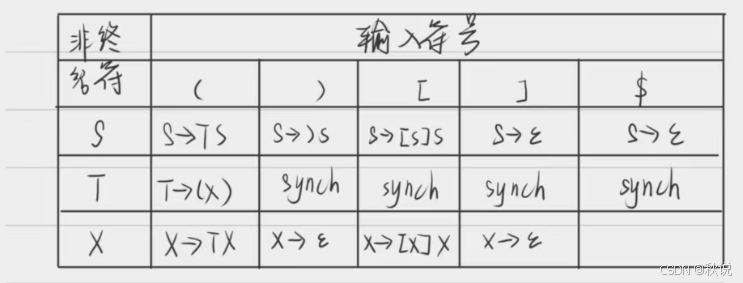
（3）此文法是LL(1)文法吗，为什么？
此文法是LL(1)文法，因为没有多重定义项目。
（4）试给出( ) [ [ ] ]的分析过程
每一步对比当前栈顶和当前输入，如果栈顶是非终结符就查表，如果不是，则直接匹配。
比如说对于第一行，栈顶是S，S是非终结符，因此查LL(1)分析表，input中第一个是(，所以定位LL(1)分析表中的S->TS，将stack改为第二行的TS$，并且input不变，action增加。

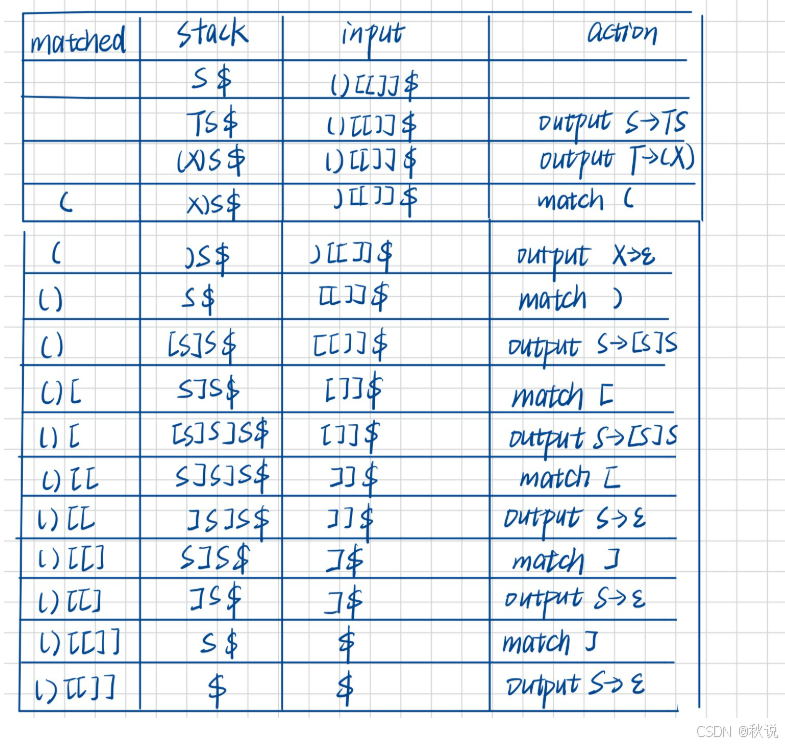
（5）试给出( [ [ ) ] ]的分析过程

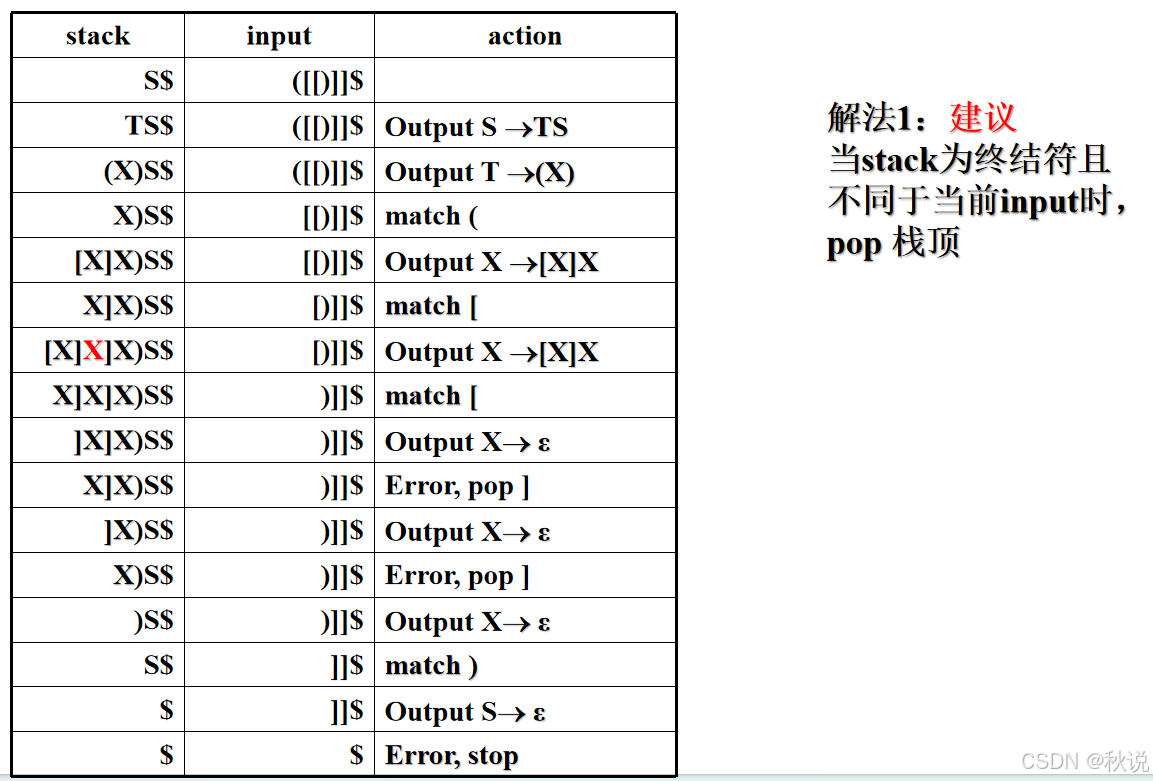
最后一行，pop栈顶，即pop $，后续无法匹配，出错，Stop。

求LL(1)预测分析表并分析输入(2)

某文法G为：


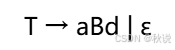
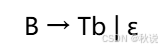
构建预测分析表，G是LL(1)文法吗？

分析表无多重定义项目，因此为LL(1)文法。

求短语、句柄、可归前缀、可行前缀(1)

1.可行前缀也称为活前缀
2.可归前缀是最长的可行前缀，即最长的活前缀
3.一个句型的最左直接短语称为该句型的一个句柄。
4.如果文法是二义的，则最右推导不止一个，可能存在多个句柄。如果文法没有二义，那么只有唯一的句柄。

对于以下文法


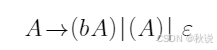
(1)对于右句型(b(A))b，给出短语，直接短语，句柄，可行前缀和可归前缀。
解：
解题顺序是：
画出分析树、找出短语、找出句柄、找出可归前缀、确定可行前缀
先画出分析树

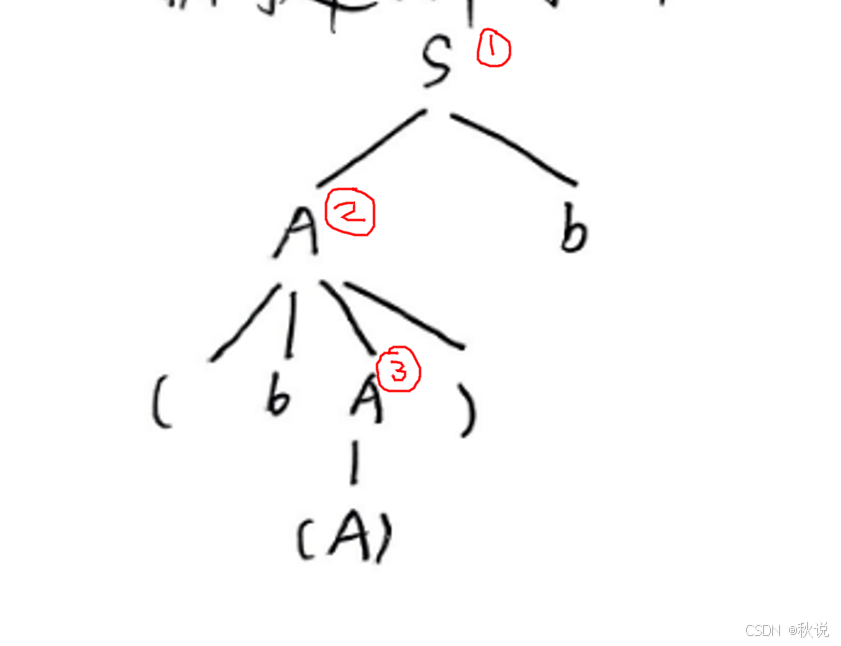
1.这棵分析树一共有3个内部结点S、A、A，以每个内部结点的叶就是一个短语。因此短语有：(A)、(b(A))、(b(A))b
2.这棵树中高度为1的子树只有一个，即3号内部节点对应的子树，它的叶是(A)，这是直接短语。如果有多个直接短语的话，最左直接短语是句柄。因此直接短语、句柄是：(A)
3.找到句柄后，就能得到可归前缀，可归前缀是以句柄结尾的前缀，即(b(A)
4.可行前缀是可归前缀的前缀，即( (b (b( (b(A (b(A) 以及空

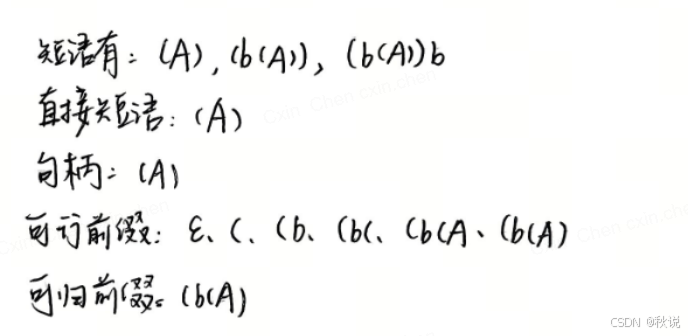
求短语、句柄、可归前缀、可行前缀(2)

现有文法G[S]:


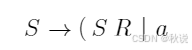
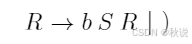
(1)给出右句型(Sb(SR)的短语、简单短语、句柄、可行前缀和可归前缀

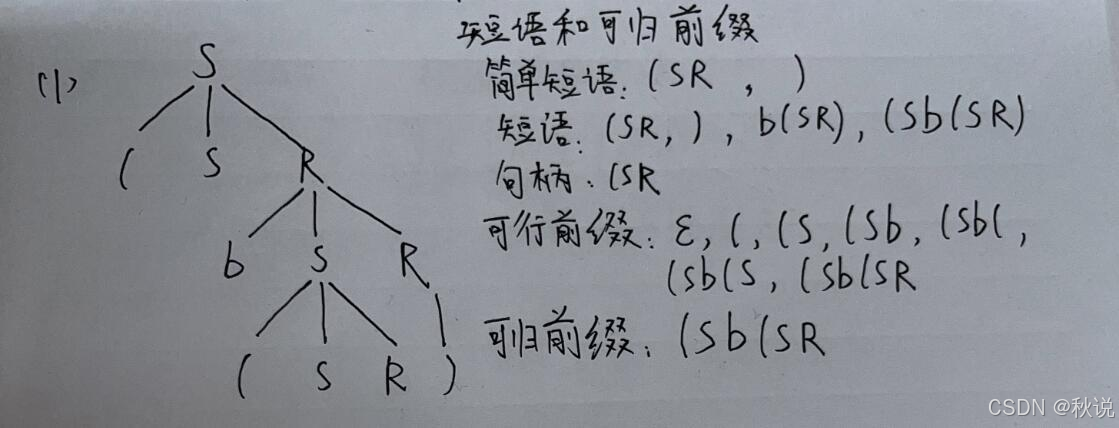
(2)给出右句型((Sba))的短语、简单短语、句柄、可行前缀和可归前缀

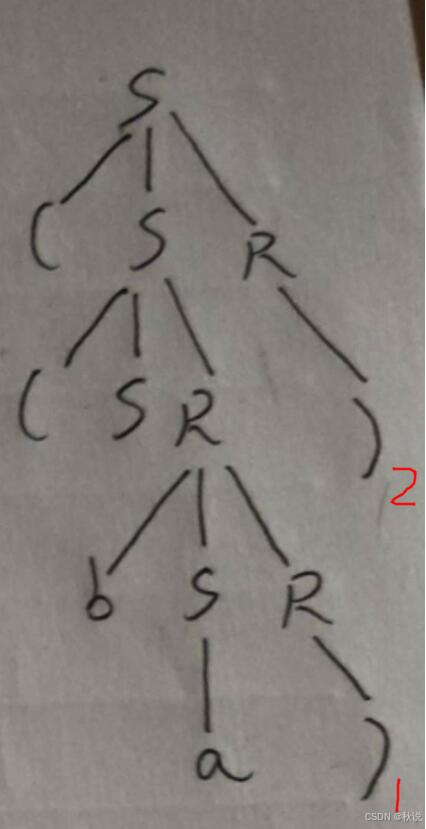
短语：a ) ) ba) (Sba) ((Sba))
简单短语：a ) )

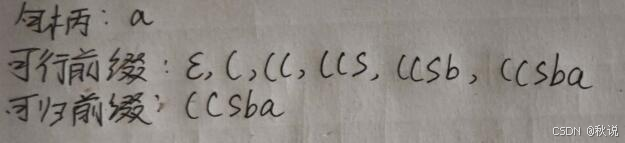
求LR(0)分析表及SLR(1)分析表

某文法G为：


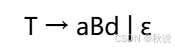
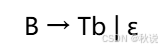
构建LR(0)分析表和SLR(1)分析表，G是LR(0)文法吗？G是SLR(1)文法吗？

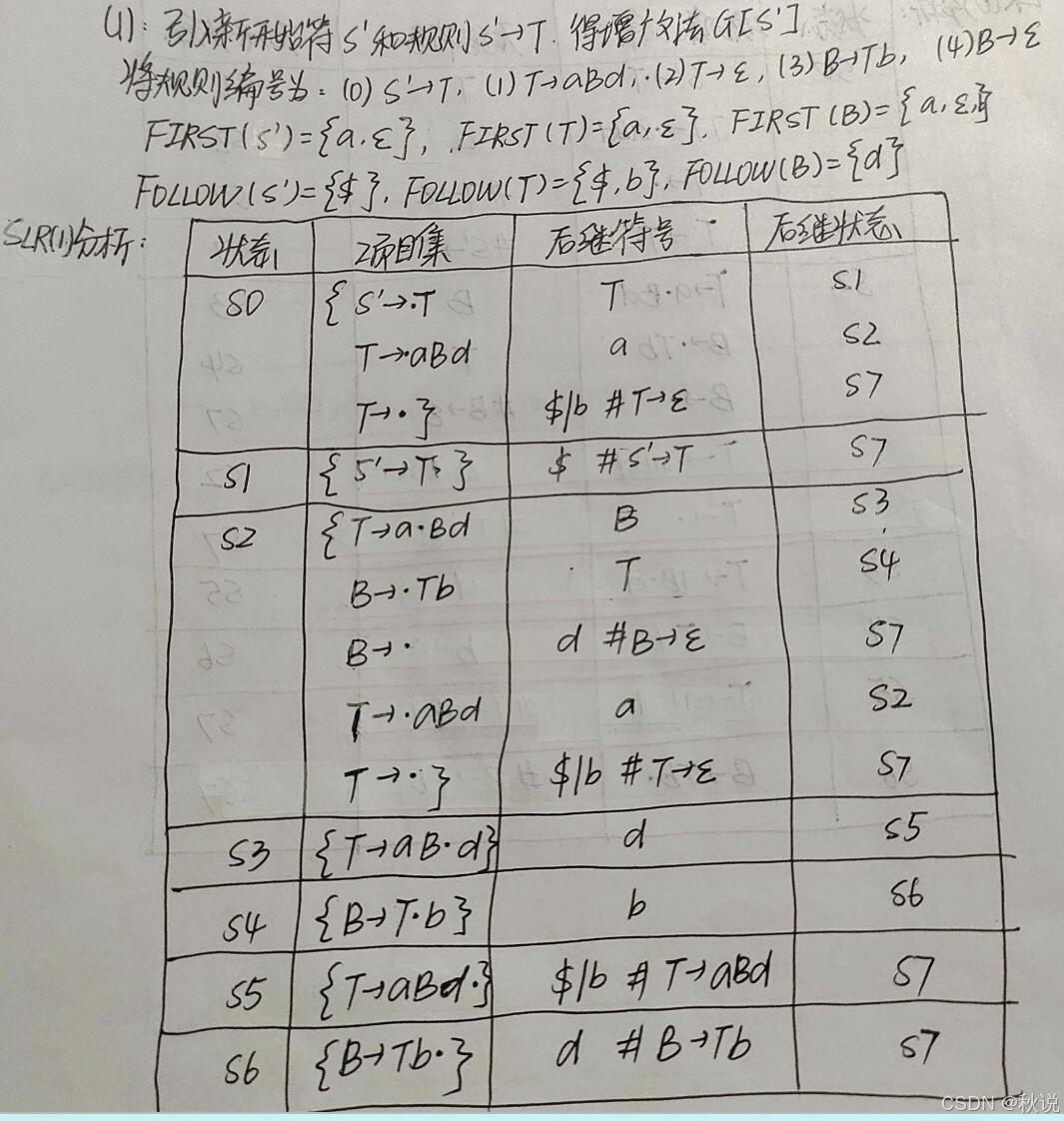
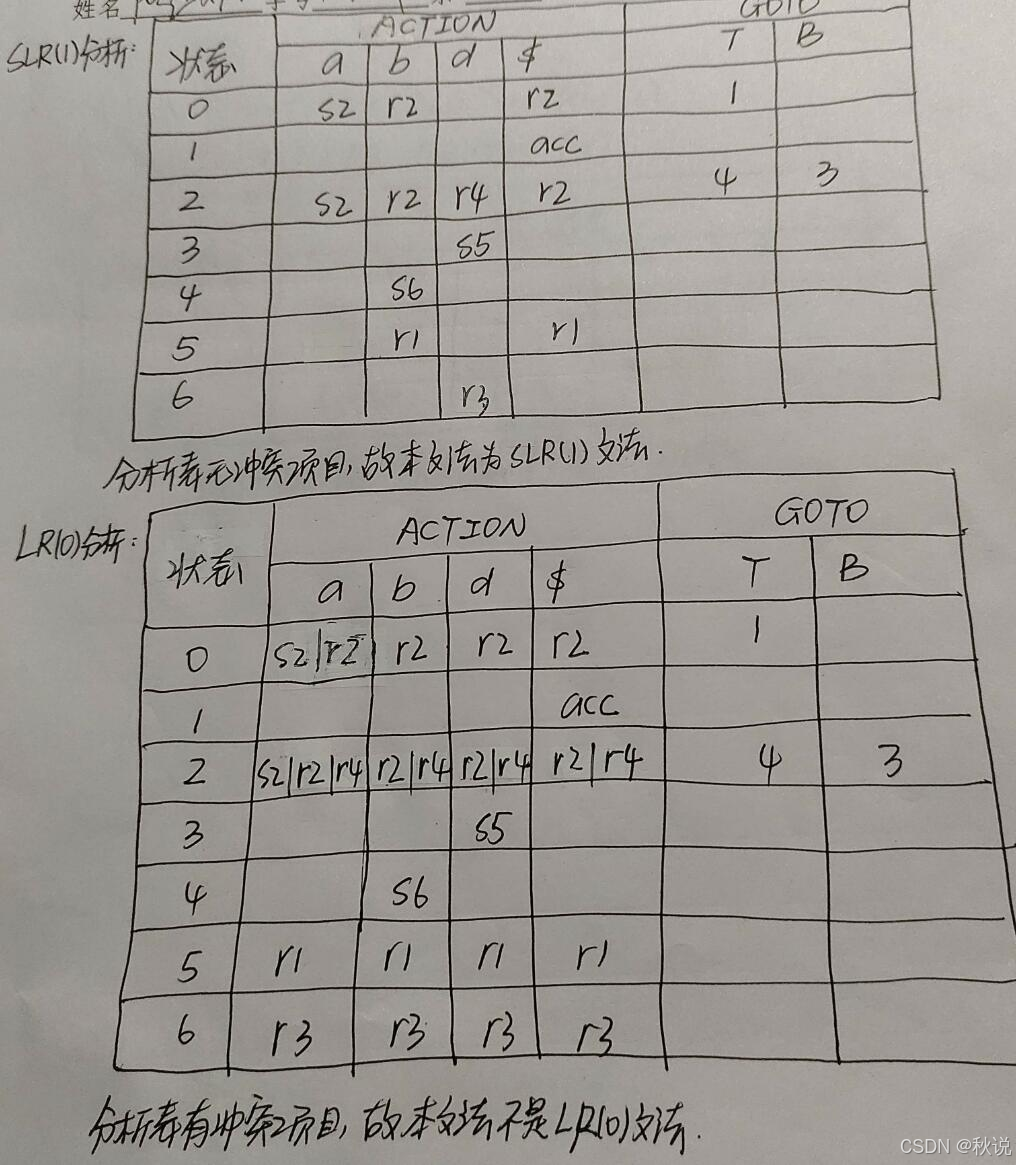
求SLR(1)分析表

考察下面关于表达式的文法：

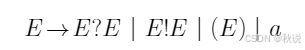
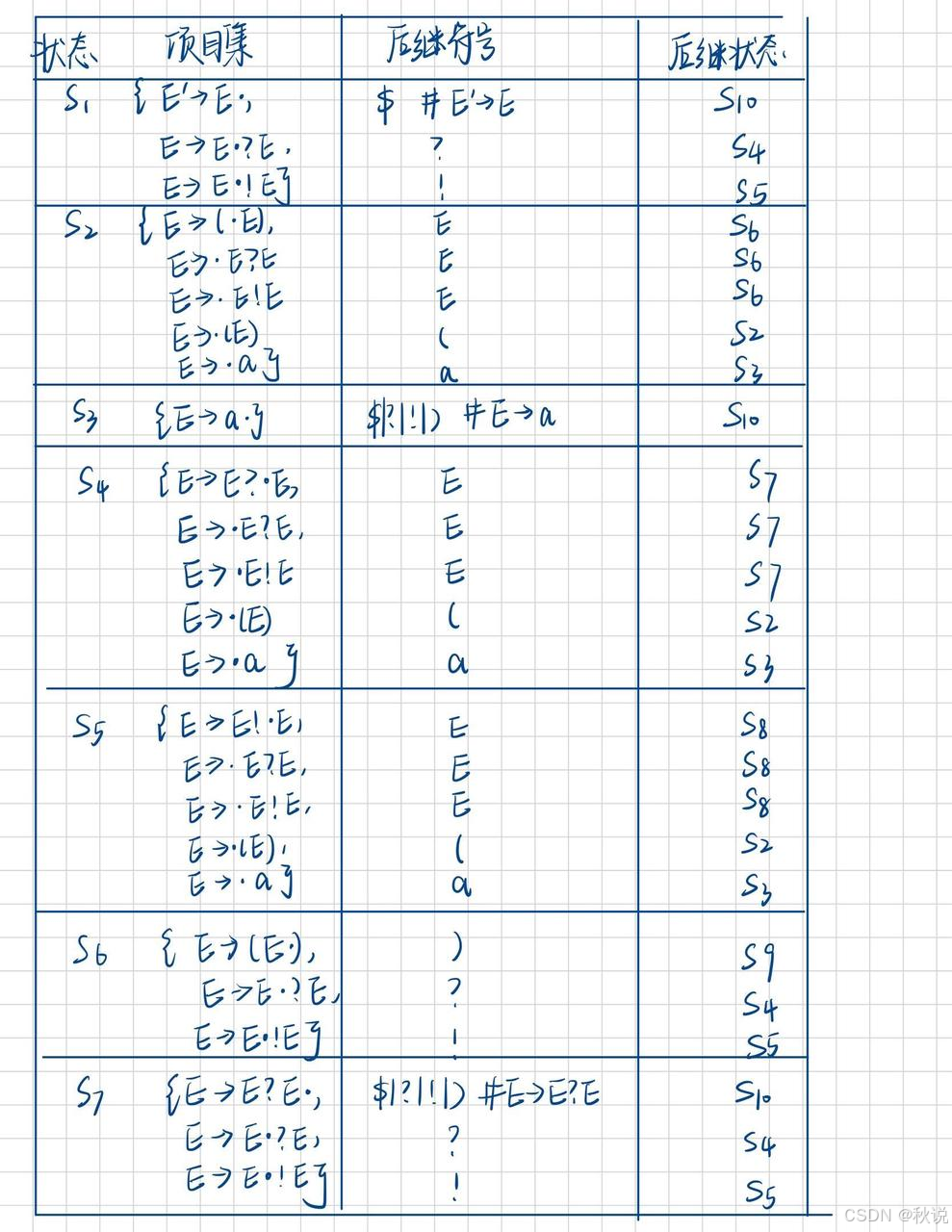
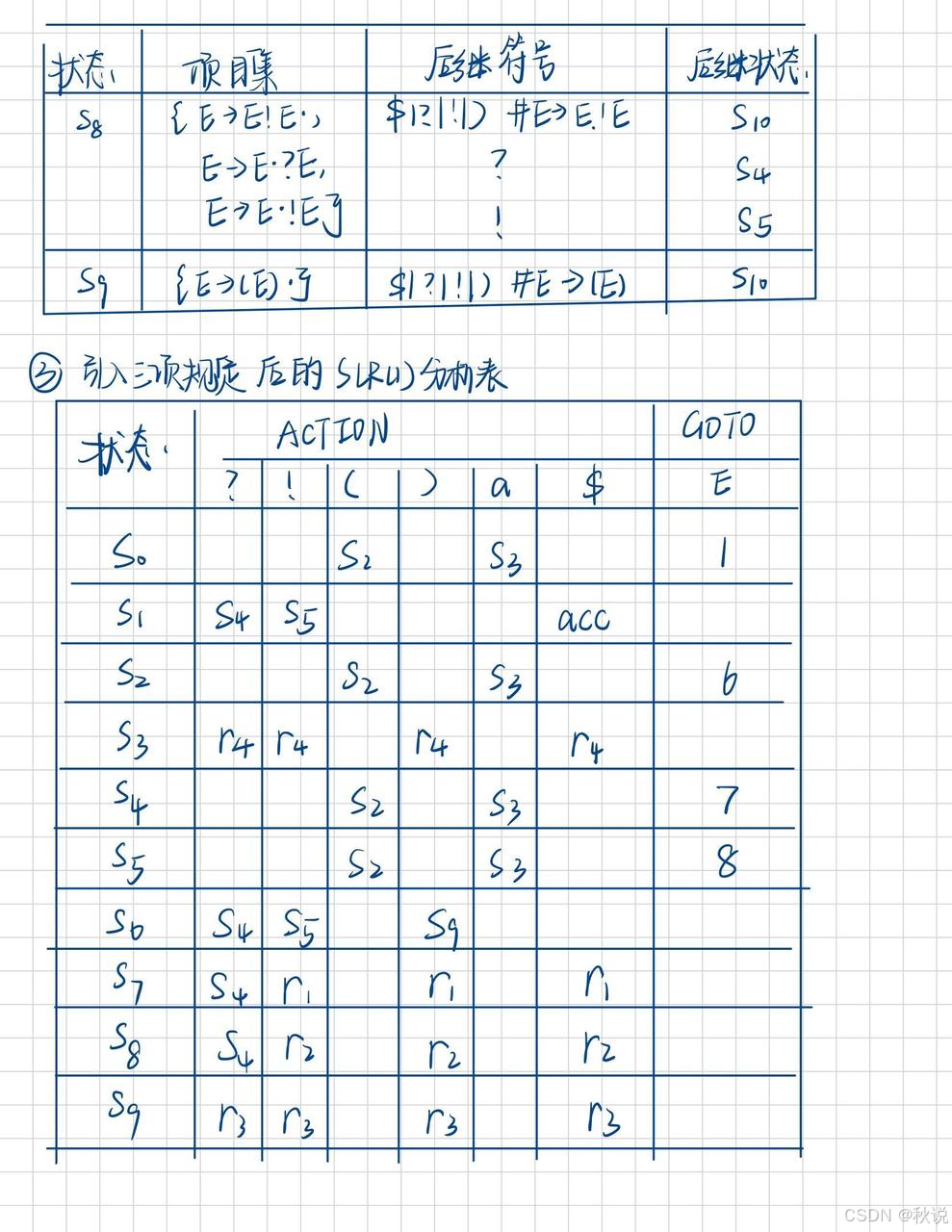
假设有以下三项规定：
？的运算优先级高于！，
？满足右结合，
！满足左结合。
试构造该文法的无冲突的SLR(1)分析表。

求LR(1)分析表及LALR分析表

对于以下文法：


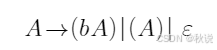
试构建LR(1)分析表
先构建增广文法，并对规则编号：

构建LR(1)自动机：

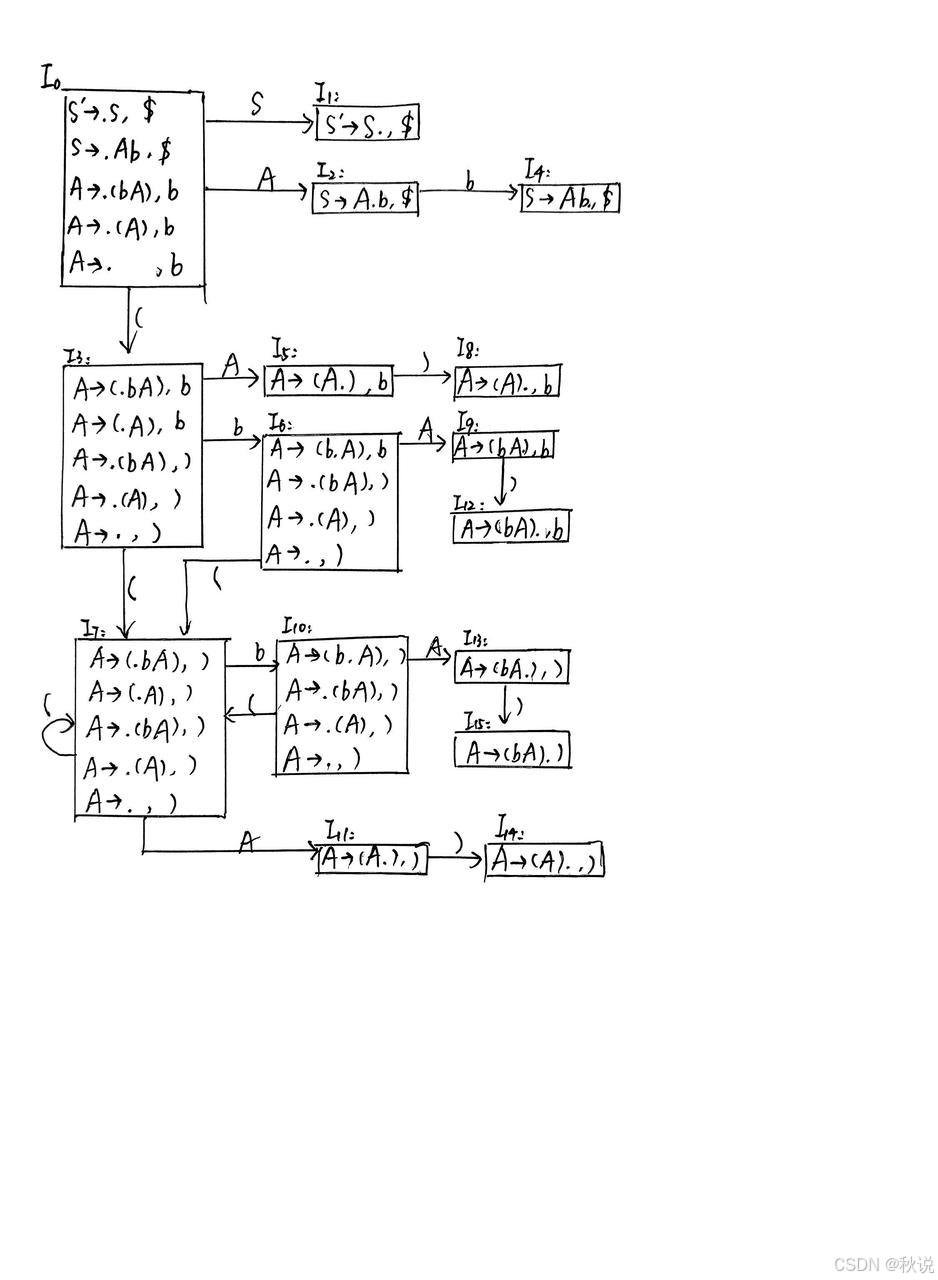
构建LR(1)分析表：
I0中的 A->· 已走完，因此在b列写上A->·对应的编号，即r4

(3)给出(b())b的分析过程

(4)试构建LALR(1)分析表，本文法是LALR(1)分析表吗，为什么？
先找到同心集（核相同的状态集）
A->B·A 与 A->BA· 不能算核相同

五种语法方法的区别

判断综合属性、继承属性(1)

终结符有综合属性、没有继承属性。
文法开始符无继承属性。
R1.a 和 R2.a 是相同的属性。

对于以下语法制导定义，有哪些继承属性，有哪些综合属性。

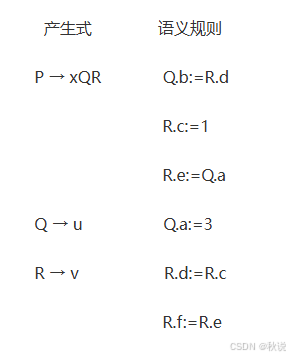
等于号左边的字母如果在产生式的右边，那它是继承属性，否则是综合属性。
例如第一条文法规则中等于号左边是Q.b，R.c，R.e。由于Q和R均在产生式右部出现，所以这3个属性全是继承属性。
综上所述，继承属性有Q.b R.c R.e，综合属性有Q.a R.d R.f

判断综合属性、继承属性(2)

考虑非终结符 A、B 和 C，A 有继承属性 a 和综合属性 b，B 有综合属性 c，C 有继承属性 d。产生式 A→BC 不可能有以下规则的哪一个？
① C.d = B.c + 1
② A.b = A.a + B.c
③ B.c = A.a
答案：规则③不可能。
解析：先画出分析树。继承属性由父 / 兄弟节点传递，综合属性由子节点传递给父节点。B 的综合属性 c 不能由父节点 A 的继承属性 a 直接赋值（违反属性依赖方向），而①（C 的继承属性 d 用 B 的综合属性 c 计算）、②（A 的综合属性 b 用自身继承属性 a 和 B 的综合属性 c 计算）均符合依赖规则。

写出语法树、四元式、三元式、间接三元式(1)

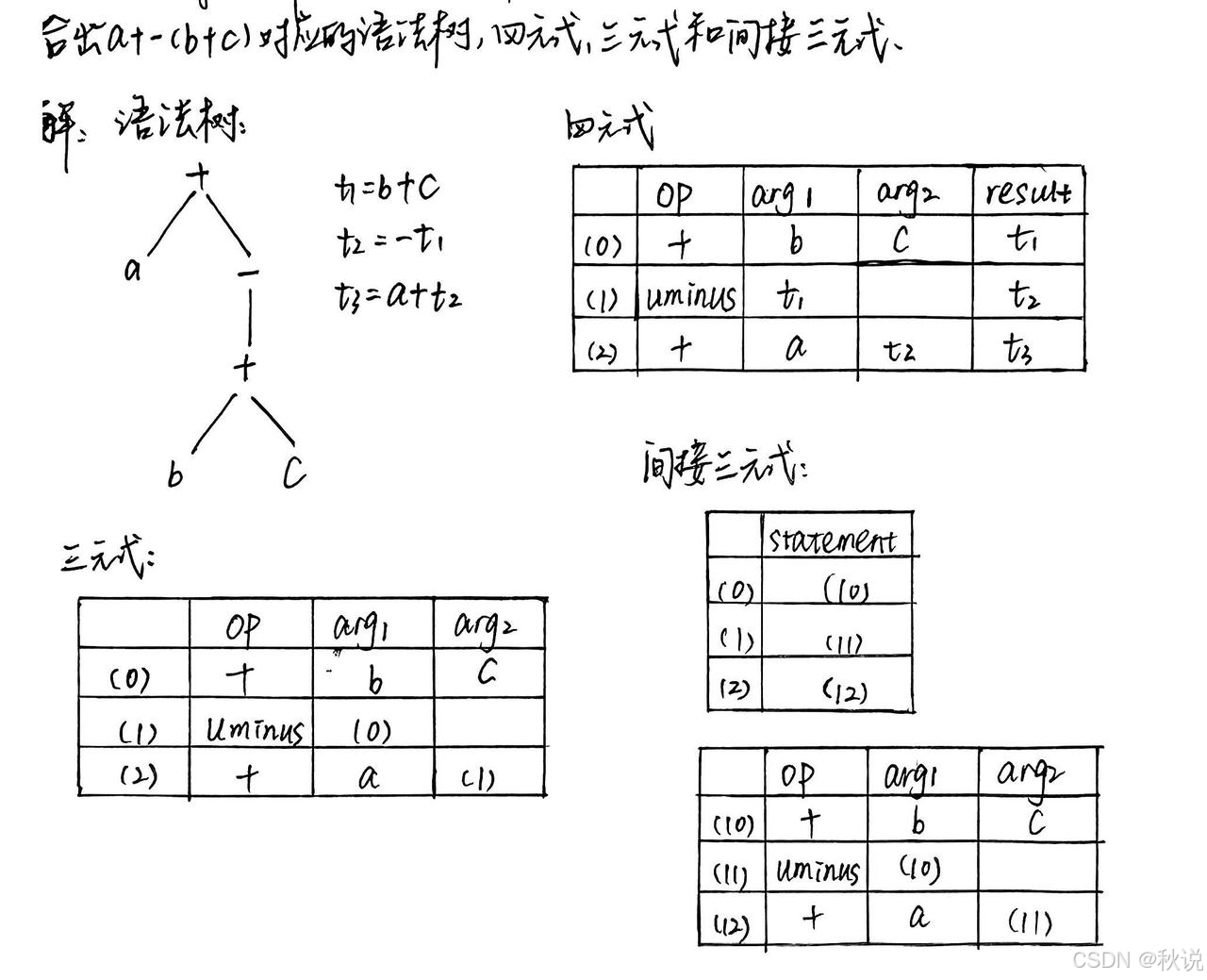
写出语法树、四元式、三元式、间接三元式(2)

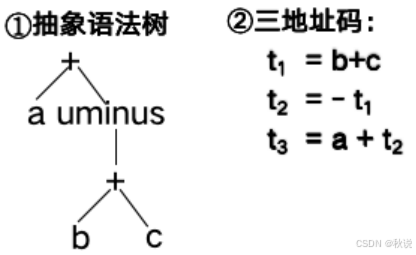
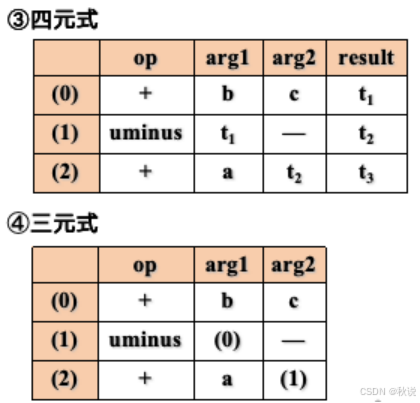
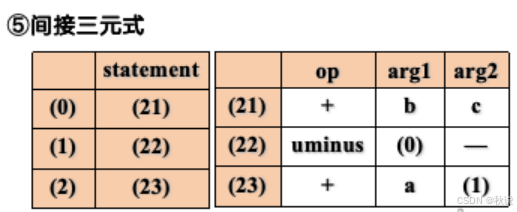
写出类型表达式(1)

给出下面类型的类型表达式及其树形表示
（1）一个函数，它的形参是两个浮点型的变量，它的返回值是一个整数（域名为a)和一个字符（域名为b)组成的记录。

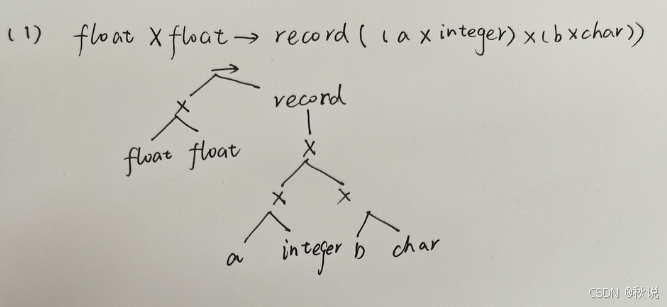
（2）一个含有10个元素的数组，每个元素是指向实数的指针。

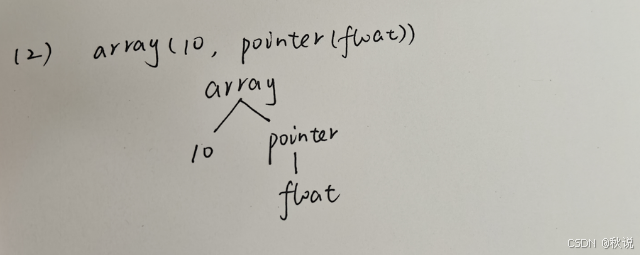
写出类型表达式(2)

答：
array(3,array(4,real))
(integer x integer) -> real

写出类型表达式(3)

答：
array(3,array(5,real))
record((x × real) × (y × real))
integer × pointer(integer) → array(20, char)

写出语法树、DAG图、记录数组(1)

给出下列表达式的语法树，后缀表达式和DAG，并基于值编码给出DAG对应的记录数组

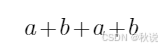
解：
先画语法树，通过后根遍历得到后缀表达式，然后得到DAG图。

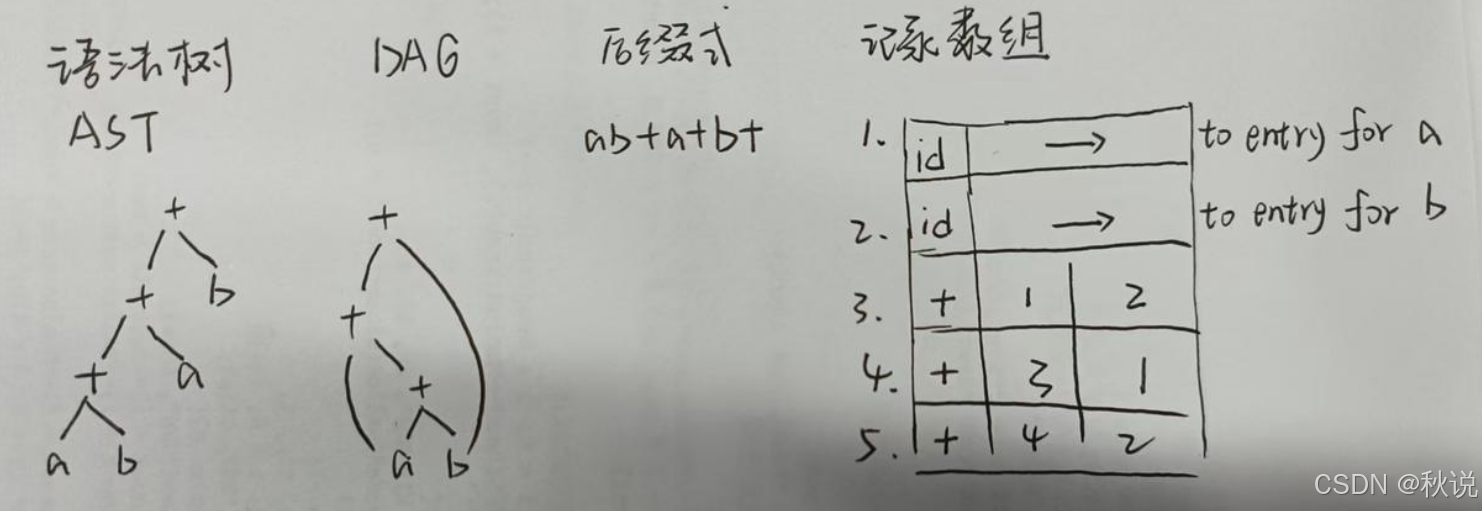
写出语法树、DAG图、记录数组(2)

给出下列表达式的语法树，后缀表达式和DAG，并基于值编码给出DAG对应的记录数组

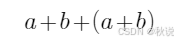
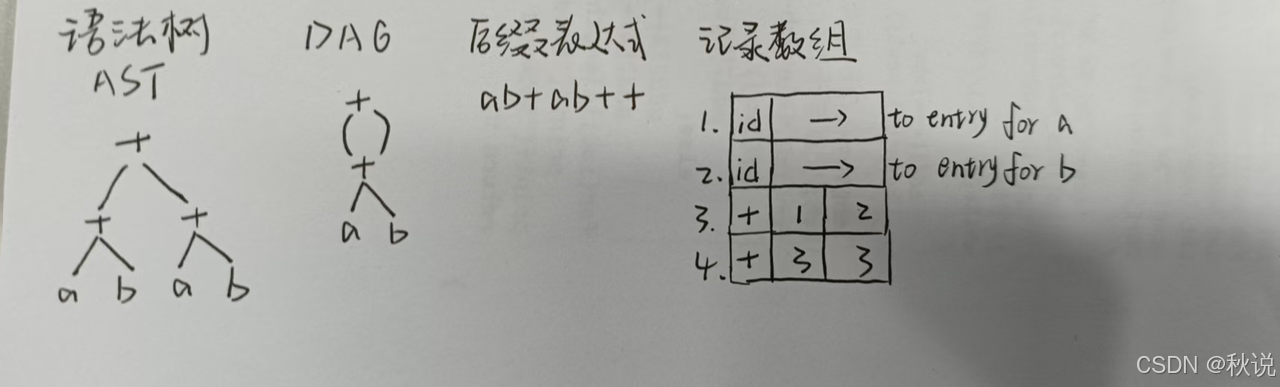
写出语法树、DAG图、记录数组(3)

给出下列表达式的语法树，后缀表达式和DAG，并基于值编码给出DAG对应的记录数组

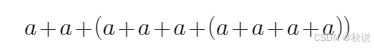
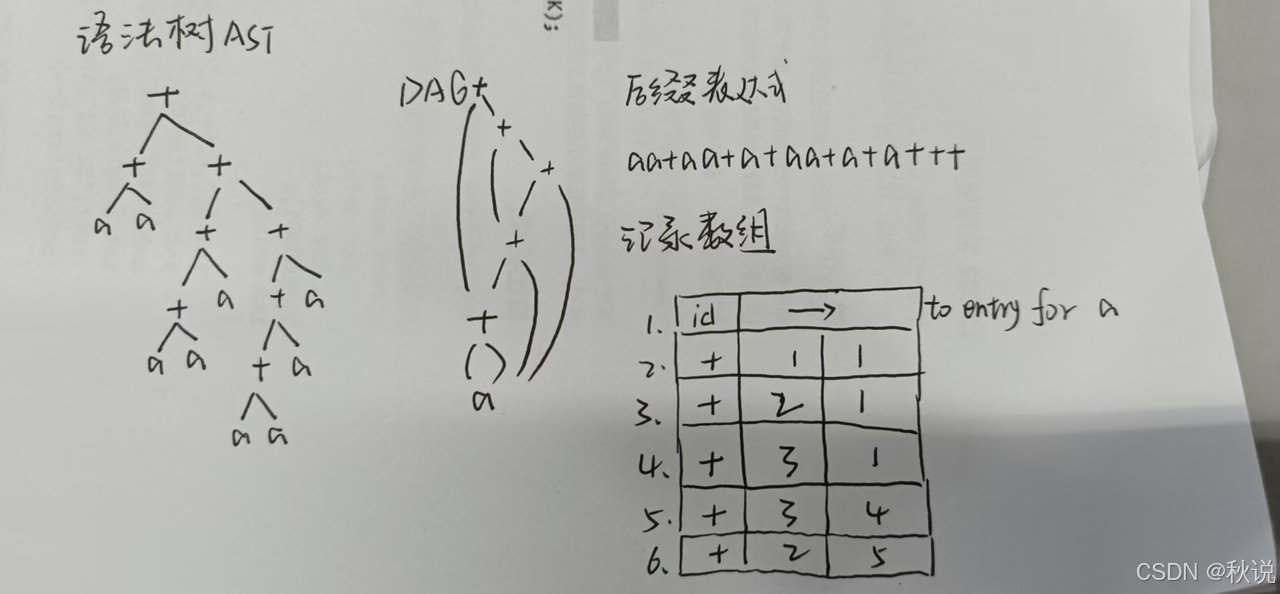
改写SDD为SDT

将以下SDD改写为SDT

语法规则中存在E的赋值和E’的赋值，若箭头右侧存在E’，那么就把E’的赋值放在E’的前面，E则放在最后。

写出语句对应的SDD

写出以下语句的SDD
S→repeat S1 until C
解：
题目逻辑为反复执行S1（至少执行一次），直到C为真时结束。

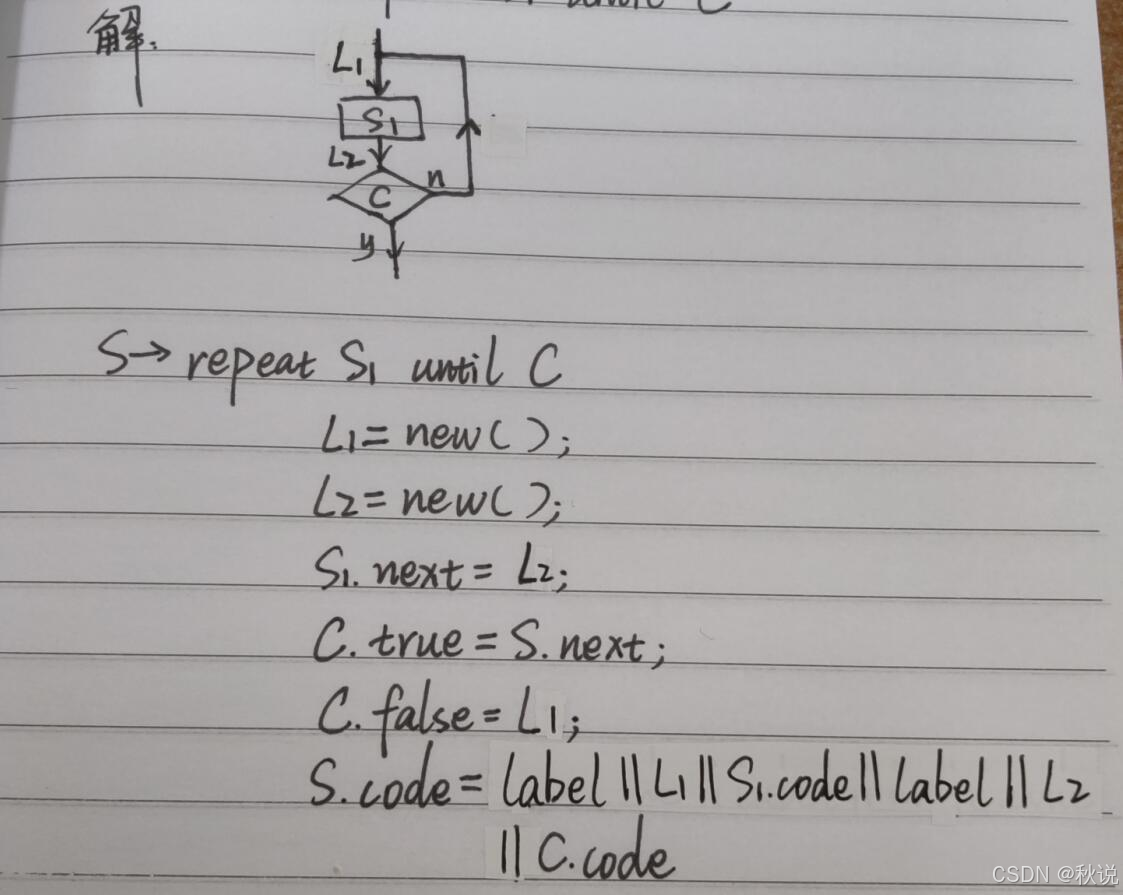
S->repeate S1 until C
L1=new(); //循环起始点
L2=new(); //条件判断点
S1.next=L2; //S1执行完后跳转至L2
C.true=S.next; //条件C为真时，跳转到S的后续代码
C.false=L1; //条件C为假时，跳转到L1（即循环起始处）
S.code=label || L1 || S1.code || label2 || L2 //生成的代码序列：标签L1 → 循环体S1 → 标签L2 → 条件判断C

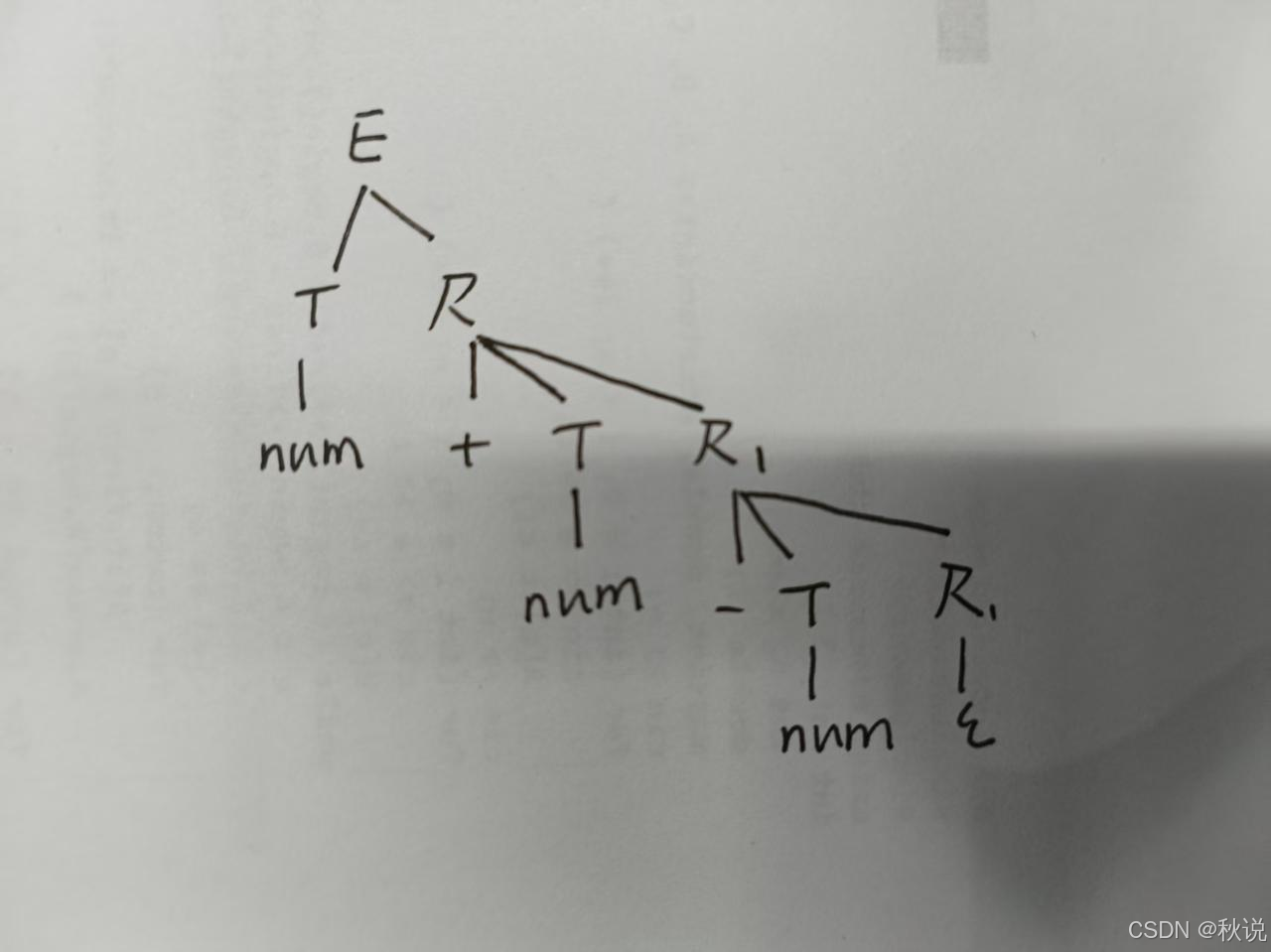
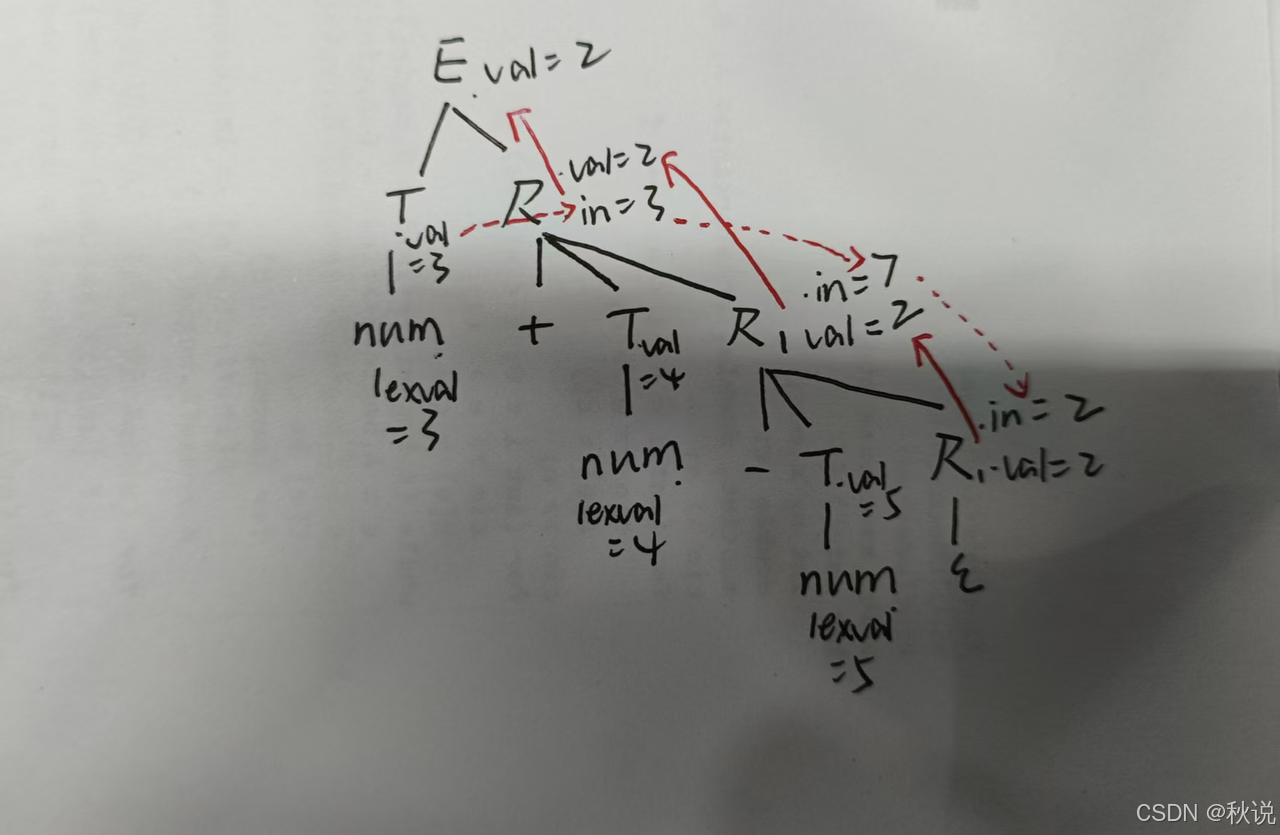
画出注释分析树(1)

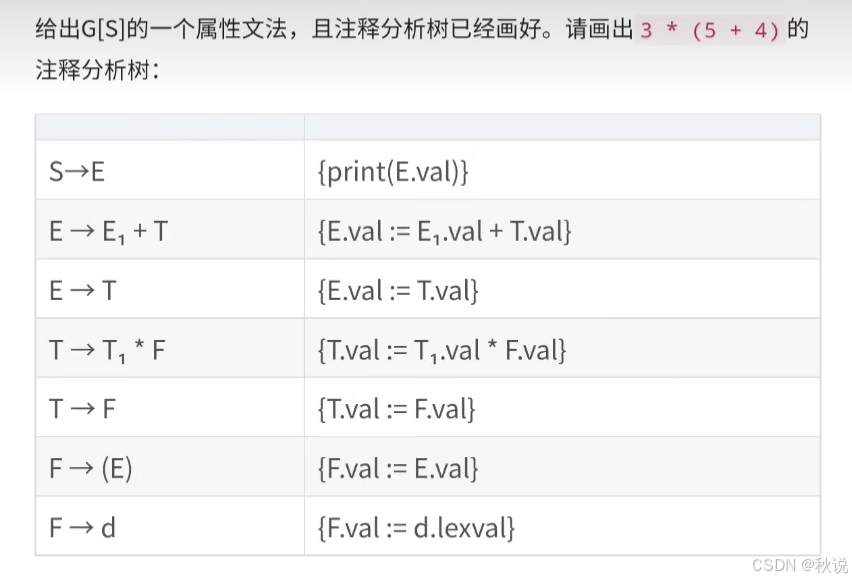
第一步：画出分析树

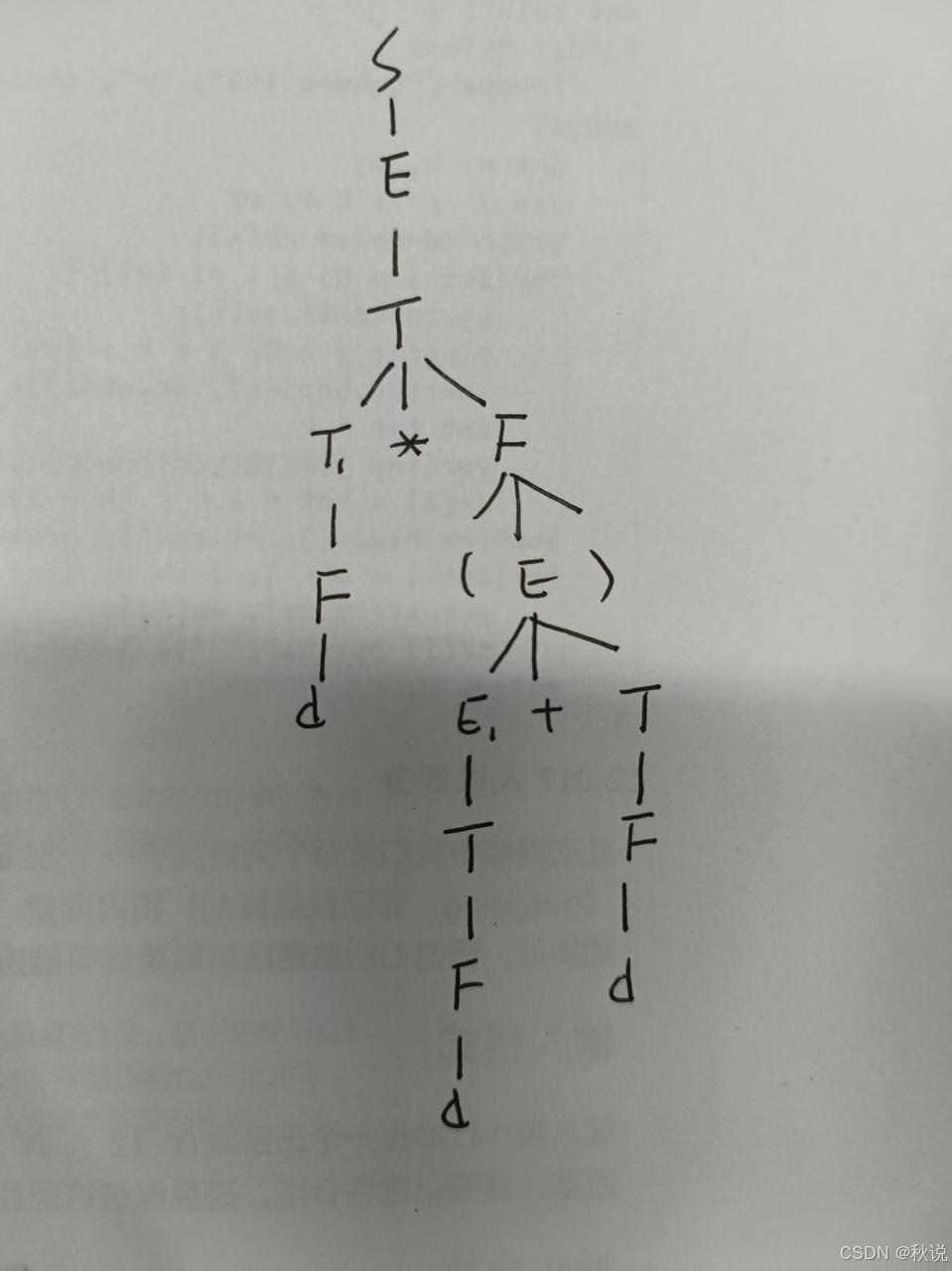
第二步：加上属性，得到注释树

画出注释分析树(2)

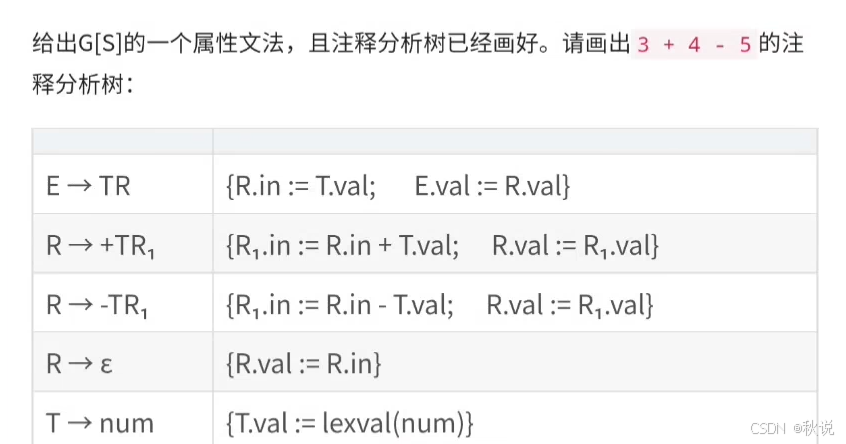
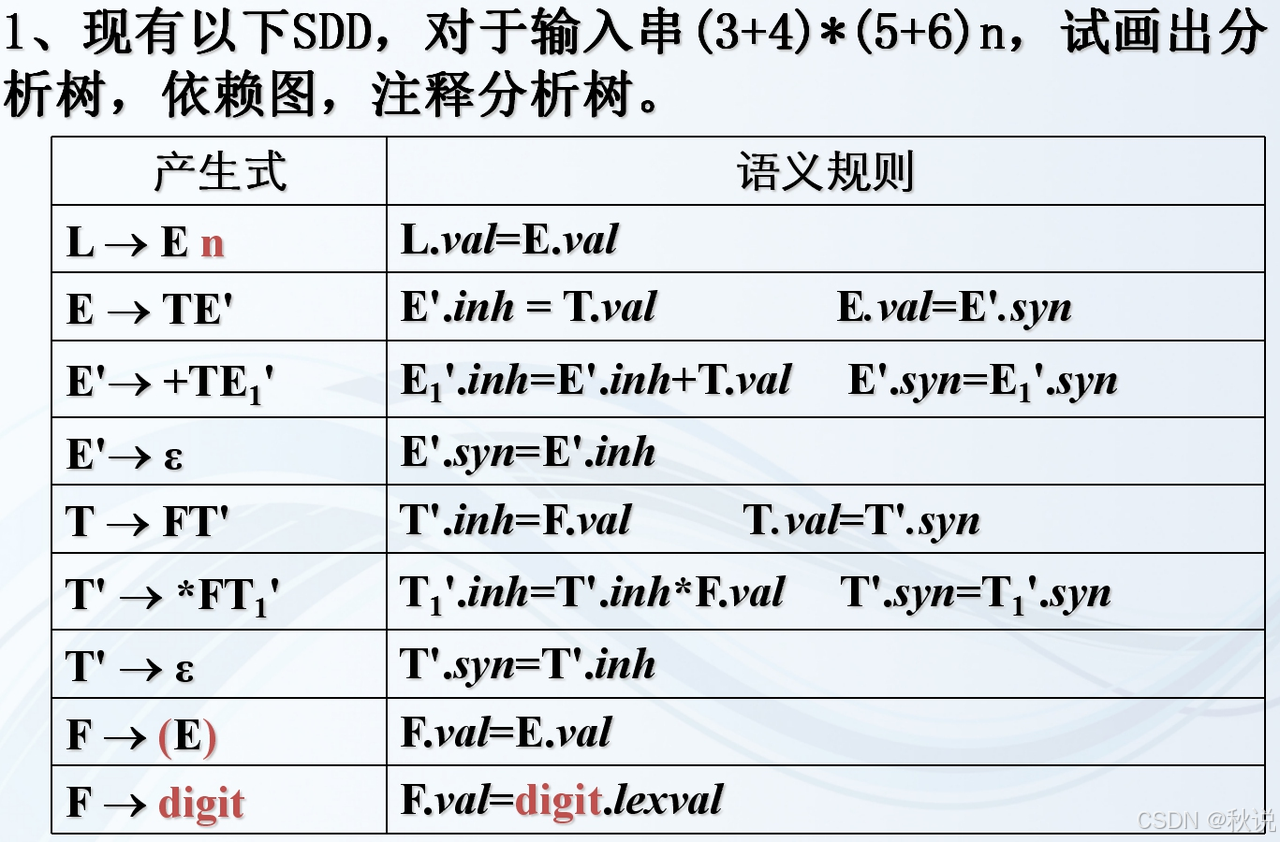
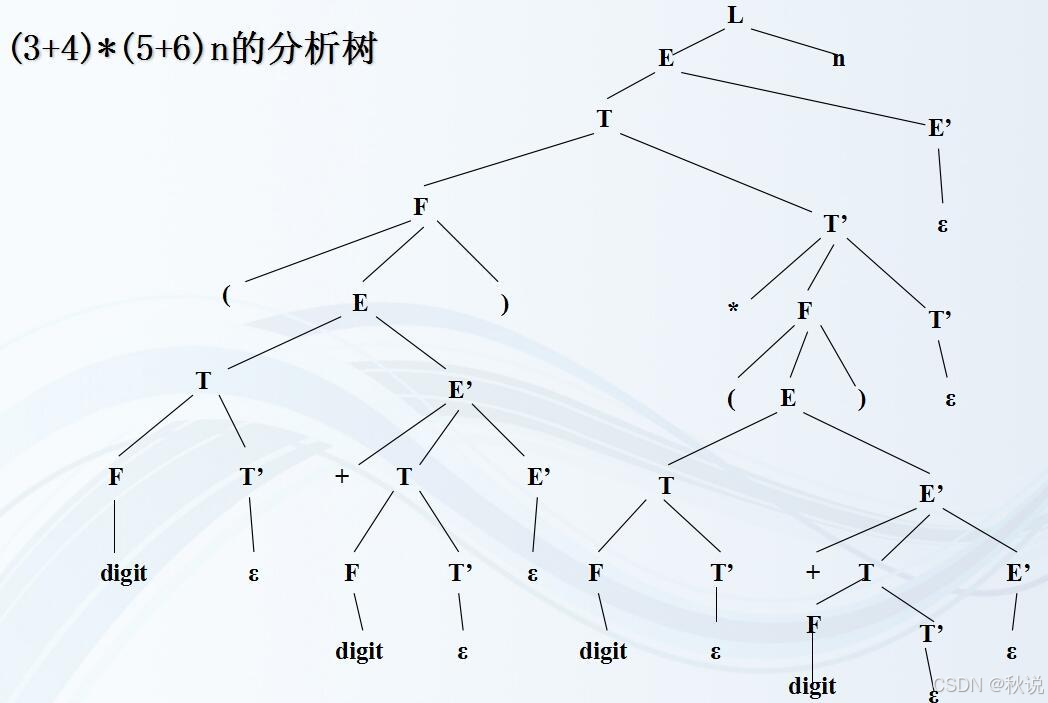
画出分析树、注释分析树、依赖图

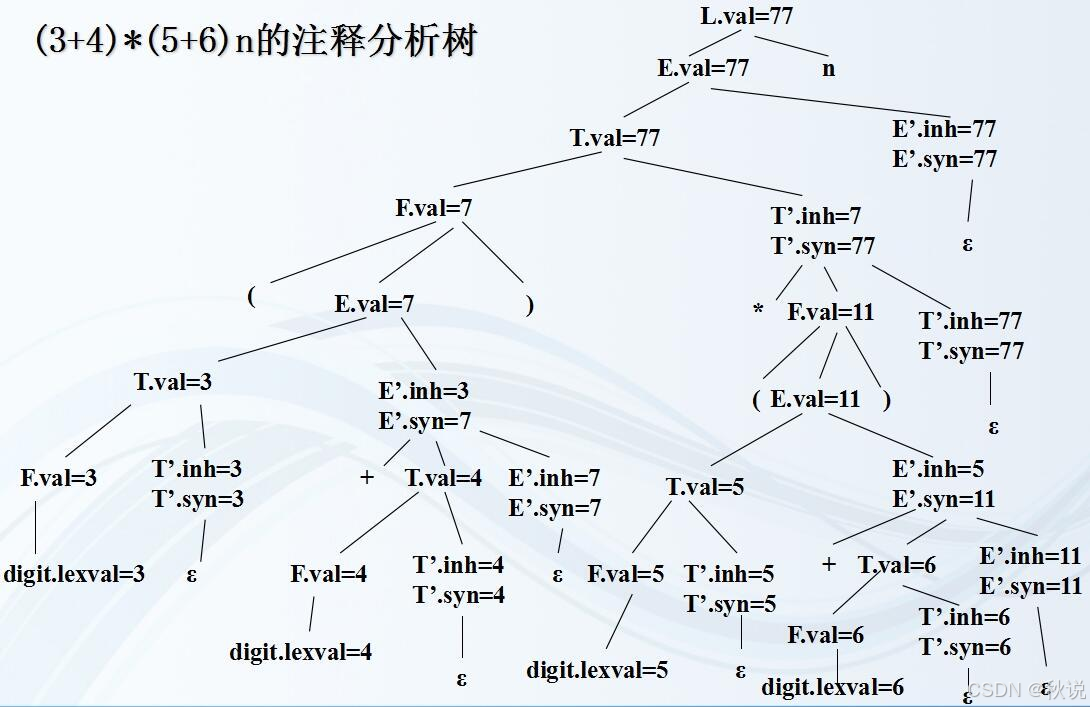
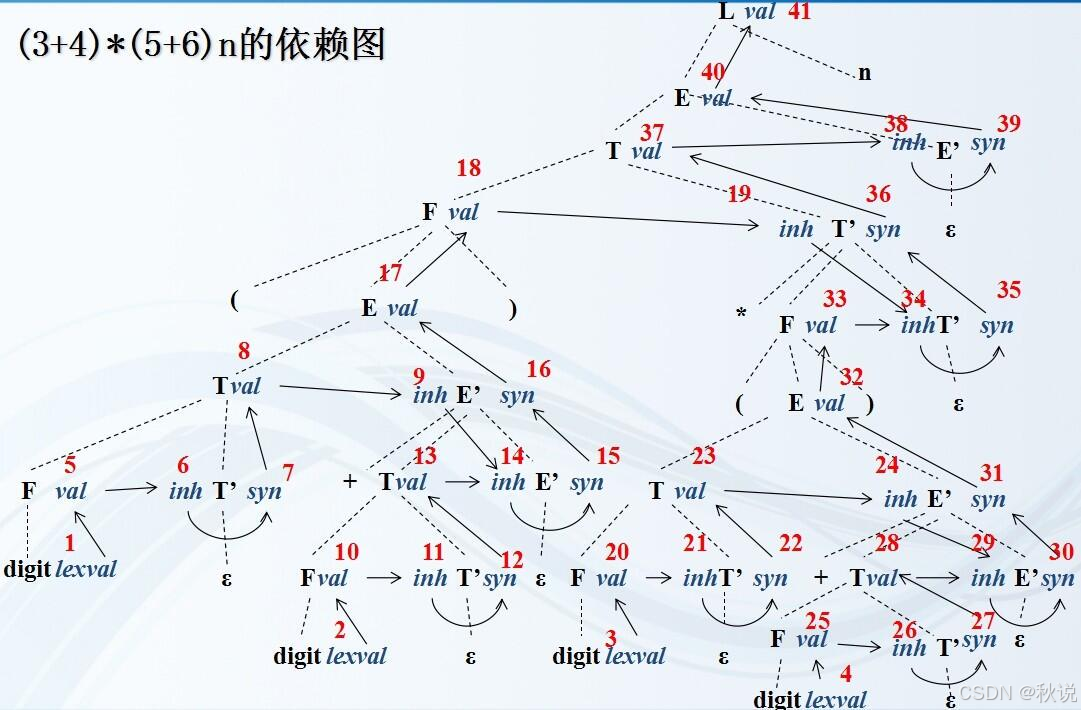
写出最左规约

给定文法:
试分析 abbcde
S>aAcBe
A→>bA-> Ab
B->d

1.先写出最右推导：S->aAcBe->aAcde->aAbcde->abbcde
2.最左规约为最右推导的逆过程
3.因此最左规约为：abbcde->aAbcde->aAcde->aAcBe->S

构建SDD、SDT

现有规则

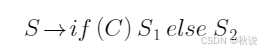
(1)请构建翻译该规则的SDT
先画流程图，再写SDD，然后构建SDT

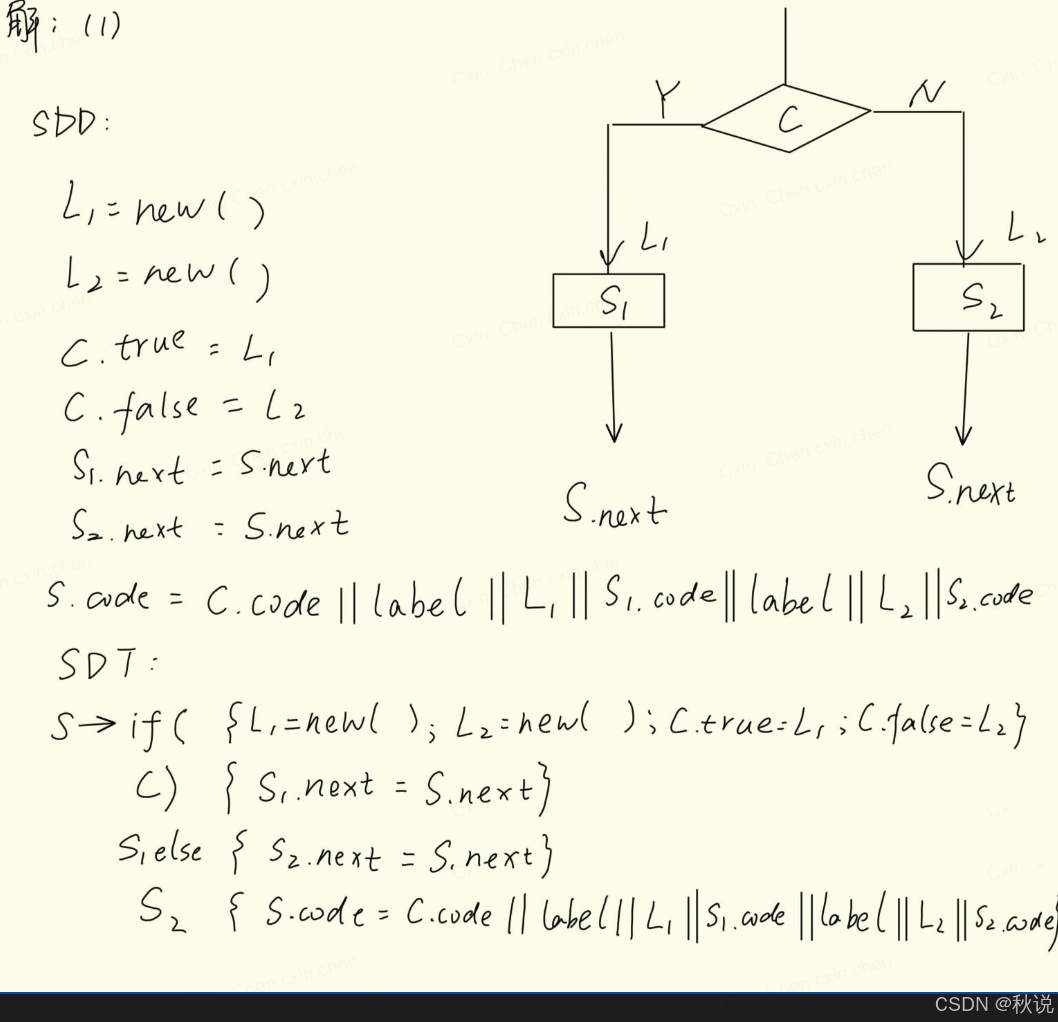
写SDT时把C.true，C.false的赋值放在C之前，S1.next的赋值放在S1之前，S2.next的赋值放在S2之前，S.code放在最后。
(2)请给出该SDT采用递归下降语法分析器的实现

(3)给出该SDT在LR语法分析器中的实现

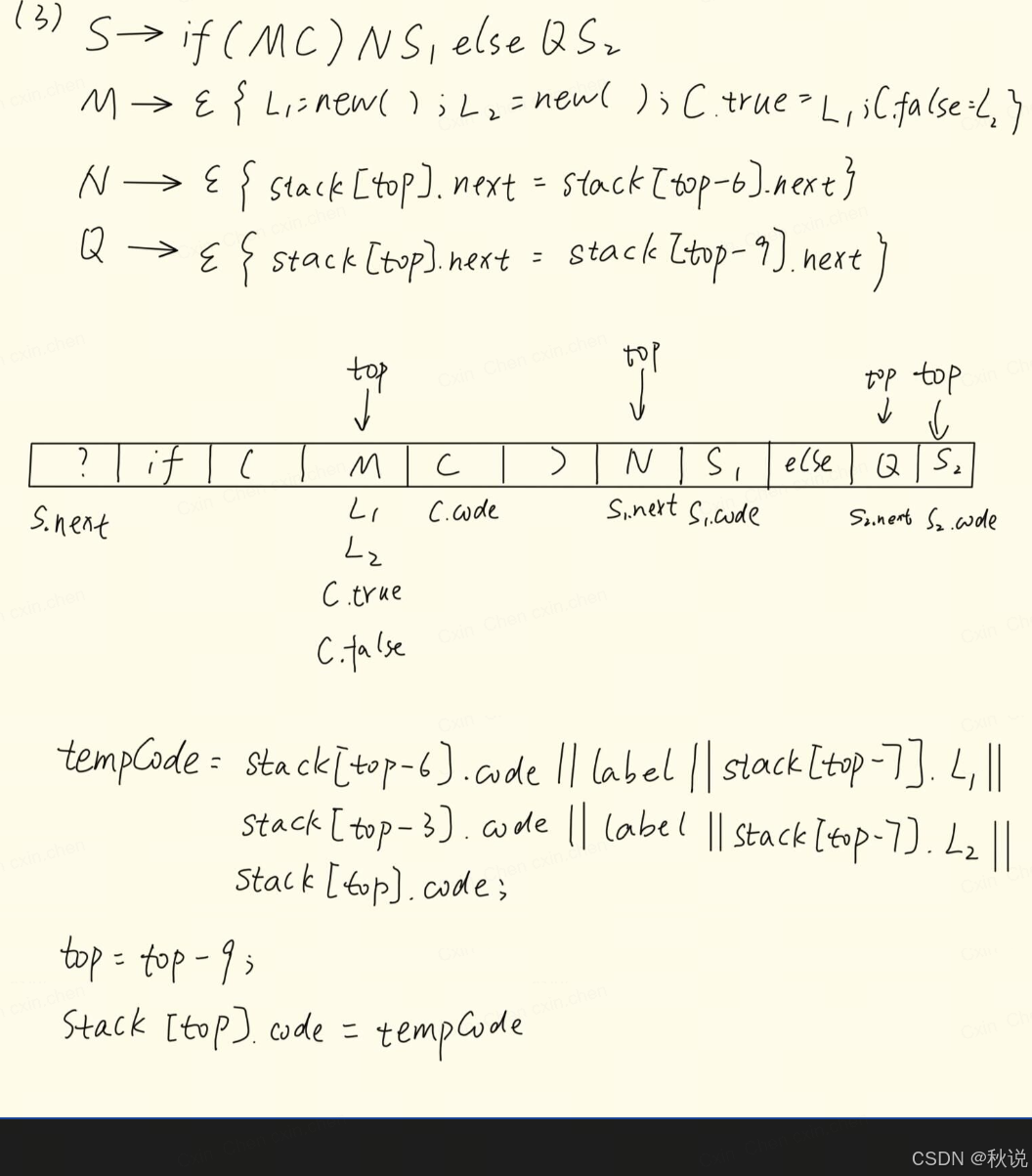
设计SDD