【数据结构入门精讲 | 第三篇】一文讲清表

在上一篇文章中我们进行了数据结构概念的练习和复杂度的计算，在这篇文章中我们将介绍表的相关知识点。

基础概念

表的定义：n(n>=0)个同一类型的元素组成的有限序列，如a(0),a(1),a(2),…,a(k),a(k+1),…,a(n)

本文将表分为顺序表和链表进行阐述。

顺序表（顺序存储）

SequenceList（顺序表）是一种数据结构，用于存储线性表的连续元素序列。它是在内存中分配一块连续的存储空间，通过数组的方式来表示线性表中的元素。顺序表中的元素在内存中是按照顺序依次存放的。

顺序表的特点是可以通过下标随机访问元素，因为元素在内存中是连续存储的。这使得顺序表在查找、访问特定位置的元素时具有高效性能。

用数组实现表时，进行插入运算所需的平均时间为O(n)；进行删除运算所需的平均时间为O(n)，所以顺序表适用于对元素的访问和查找操作较多的场景，但插入和删除操作相对较慢，因为需要移动其他元素。

链表（链式存储）

单链表

单链表是由指针实现的，用指针将存储表元素的单元依次串连在一起，就得到了链表。

基本思想如下：
用一组任意的存储单元存储线性表的数据元素 、每个表元素单元中设置指针表示表中元素之间的逻辑关系 、每个单元包括一个元素(数据域)和一个指针(指针域)，其中指针指向表中下一个元素所在的单元
注意：尾部元素的指针是空指针

• 在单链表上效率更高的操作
  • 删除所有值为x的数 O(1)
  • 删除某个任意元素 O(1)
  • 在任意元素后插入一个数 O(1)
• 在顺序表上效率更高的操作
  • 在最后一个元素后面插入一个数
  • 交换任意两个元素的值
  • 取出某个元素的值

伪代码

函数ListInit()功能：创建一个空表

List ListInit()
{
    List L = malloc(sizeof *L);
    L->first = 0;
    return L;
}

ListEmpty(L)功能：判断表首指针first是否为空指针

int ListEmpty(List L)
{
    return L->first==0;
}

ListLength(L)功能：对表进行线性扫描计算表的长度

int ListLength(List L)
{
    int len = 0;
    link p = L->first;
    while (p)
    {
        /* 自表首指针始对表L进行线性扫描计算非空指针数目即为表长 */
        len++;
        p = p->next;
    }
    return len;
} // O(n)

ListRetrieve(k,L)功能：从表首开始向后线性扫描每一个元素直到找到第k个元素

ListItem ListRetrieve(int k, List L)
{
    int i;
    link p;
    if (k < 1) {
        Error("out of bounds");
    }
    p = L->first;
    i = 1;
    while (i < k && p) {
        p = p->next;
        i++;
    }
    return p->element;
} // 若表中不存在第k个元素，返回空指针，而非错误信息
// O(n)

PrintList(L)功能：从表首元素开始线性扫描整个链表并输出每个元素

void PrintList(List L)
{
    link p;
    for (p = L->first; p; p = p->next)
    {
        ItemShow(p->element);
    }
} // O(n)

ListInsert(k,x,L)功能：插入元素x到第k个元素之后。

void ListInsert(int k, ListItem x, List L)
{
    link p, y;
    p = L->first;
    for (int i = 1; i < k && p; i++)
    {
        p = p->next;
    }
    // 自表首始找插入位置
    y = NewNode();
    y->element = x;
    if (k) // 在位置p处插入节点y
    {
        y->next = p->next;
        p->next = y;
    }
    else // 在表首插入需要特殊处理
    {
        y->next = L->first;
        L->first = y;
    }
} // O(k)

ListDelete(k,L)功能：删除第k个元素

ListItem ListDelete(int k, List L)
{ 
    link p, q; 
    ListItem x; 
    int i;
    if (k < 1 || !L->first) 
        Error("out of bounds");
    p = L->first;
    if (k == 1) 
    {
        L->first = p->next; // 删除表首元素需要特殊处理
    } 
    else 
    {
        q = L->first; //自表首始找表中第k-1个元素所在结点q
        for (i = 1; i < k - 1 && q; i++) 
        {
            q = q->next; 
        }
        p = q->next; //让p指向 第k个元素所在结点
        q->next = p->next; // 删除结点p
    }
    x = p->element; // 第k个元素存⼊x并释放结点p
    free(p);
    return x;
}//o(k)

---

下面介绍三个对链表的简单处理

删除链表倒数第n个节点

    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* newhead=new ListNode(0);
        newhead->next=head;
        ListNode* fast=newhead;
        ListNode* slow=newhead;
        while(fast!=nullptr&&n--)   fast=fast->next;
        fast=fast->next;
        while(fast!=nullptr)
        {
            fast=fast->next;
            slow=slow->next;
        }
        slow->next=slow->next->next;
        return newhead->next;
    }

合并两个有序链表

//将两个有序链表合并为一个升序链表，在两个有序链表间加上next关系即可
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        if(list1==NULL&&list2==NULL) return NULL;
        ListNode* head=new ListNode(-1);
        ListNode* prev=head;
        while(list1!=NULL&&list2!=NULL)
        {
           if(list1->val>=list2->val)
           {
               prev->next=list2;
               list2=list2->next;
           }else
           {
               prev->next=list1;
               list1=list1->next;
           }
           prev=prev->next;
        }
        if(list1!=NULL) prev->next=list1;
        else prev->next=list2;

        return head->next;
    }

反转链表

    ListNode* reverseList(ListNode* head) {
        ListNode* pre=NULL;
        ListNode* tmp;
        ListNode* cur=head;
        while(cur)
        {
            tmp=cur->next;
            cur->next=pre;
            pre=cur;
            cur=tmp;
        }
        return pre;
    }

单循环链表

以上为单链表的讲解，现在让我们开始单循环链表的介绍。

由于单链表中最后一个元素所在的单元的指针为Null，当我们将其指向表首单元时，这个链表就变成了首尾相接的链表，即单循环链表，也就是说，从任意一个单元出发，可以找到任何其它的单元。

图例如下：

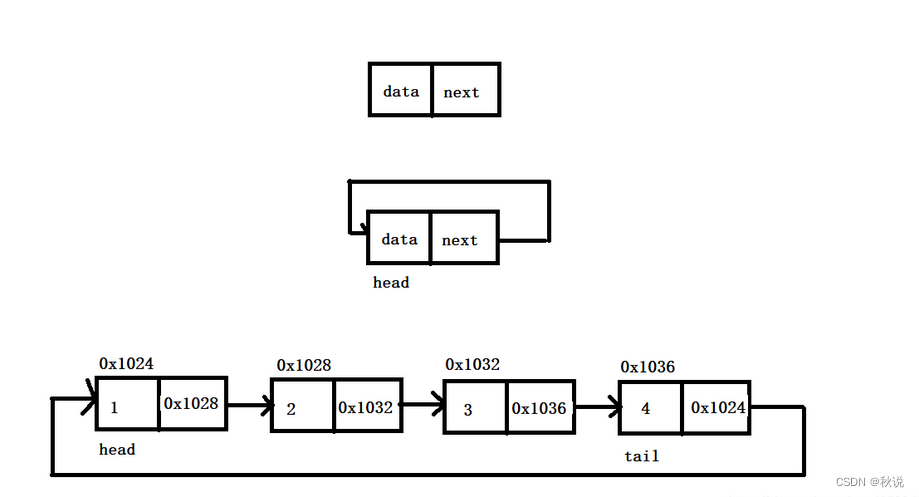
因此：含有尾指针单循环链表实现删除头节点和在尾节点后插入的操作效率最高。

伪代码

ListRetrieve(k,L) 功能：从表中第一个元素开始向后扫描直到找到表中第k个元素

ListItem ListRetrieve(int k, List L)
{
    int i = 1;
    link p;
    if (k < 1 || k > L->n)
        Error("out of bounds");
    /* Last指针指向表尾元素，必须先找到表首元素开始线性扫描 */
    p = L->last->next->next;
    // 若无头结点，该语句为 p=L->last->next;
    while (i < k)
    {
        p = p->next;
        i++;
    }
    return p->element;
}
// O(k)

ListLocate(x,L)功能：从表中第一个元素开始逐个向后进行线性扫描直到找到表中元素x，返回其位置

int ListLocate(ListItem x, List L)
{
    int i = 1;
    link p;
    /* Last指针指向表尾元素，必须先找到表首元素开始线性扫描 */
    p = L->last->next->next;
    L->last->next->element = x;
    // 查找元素x暂时置于头结点中
    while (p->element != x)
    {
        p = p->next;
        i++;
    } // 最坏情况是终⽌于头结点
    return ((p == L->last->next) ? 0 : i);
    // 若p为头结点，则表中无元素x
} // O(n)

ListInsert(k,x,L)运算功能：将元素x插入第k个元素之后

// 使用哨兵结点，无须特殊处理表首元素插入，但由于通过表尾指针维护一张单循环链表，因此需要额外处理表尾指针
void ListInsert(int k, ListItem x, List L)
{
    link p, y;
    int i;
    if (k < 0 || k > L->n)
        Error("out of bounds");
    p = L->last->next;
    for (i = 1; i <= k; i++)
        p = p->next;
    // 自表首头结点开始查找插入位置
    y = NewNode();
    y->element = x;
    y->next = p->next;
    p->next = y; // 在位置p处插⼊
    if (k == L->n)
        L->last = y; // 表尾做特殊处理
    L->n++;
} // O(k)

ListDelete(k,L)运算功能：删除表中第k个元素

// 使用哨兵结点，无须特殊处理表首元素插入，但由于通过表尾指针维护一张单循环链表，因此需要额外处理表尾指针
ListItem ListDelete(int k, List L)
{
    link p, q;
    ListItem x;
    int i;
    if (k < 1 || k > L->n)
        Error("out of bounds");
    q = L->last->next;
    for (i = 0; i < k - 1; i++)
        q = q->next;
    p = q->next; // 让p指向第k个元素所在结点
    q->next = p->next; // 删除结点p
    if (k == L->n)
        L->last = q;
    x = p->element; // 第k个元素存入x并释放结点p
    free(p);
    L->n--;
    return x;
} // O(k)

PrintList(L) 功能：从表首元素开始线性扫描整个链表并输出每个元素

void PrintList (List L)
{
 link p;
 for (p = L->last->next->next; p!=L->last->next; p = p->next)
 ItemShow(p->element);
}
//O(n)

双循环链表

双链表，即在链表的每个结点设置两个指针，一个指向后继结点，另一个指向前驱结点。

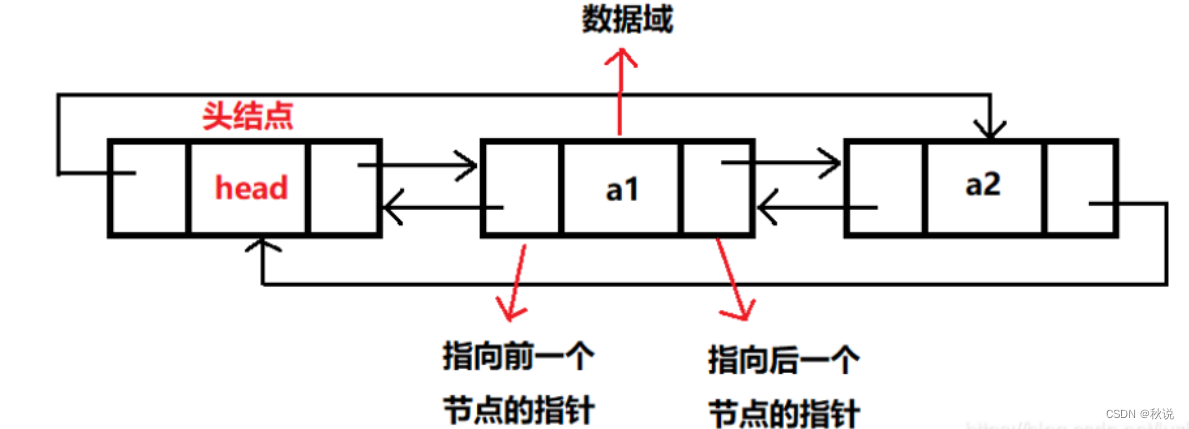
开发出双循环链表的原因在于：单链表中不能找到当前结点的前驱，而循环链表中找到其前驱的时间为O(n)，双循环链表的出现解决了该问题。

• 链表为空的标志：head->prior==head&&head->next=head
• 实现删除尾节点和在尾节点后插入的操作效率最高

在O(1)时间确定任一元素的前驱和后继元素所在的结点

伪代码

ListInit() 功能：创建一个仅由表首哨兵结点组成的空双向循环链表

List ListInit()
{
    link y;
    List L = (List)malloc(sizeof(List));
    y = NewNode(); // 采用了头结点的改进方法
    y->left = y;
    y->right = y;
    L->header = y;
    L->n = 0;
    return L;
}

ListRetrieve(k,L)功能： 从表中第一个元素开始向后扫描直到找到表中第k个元素

ListItem ListRetrieve(int k, List L)
{
    int i = 1;
    link p;
    if (k < 1 || k > L->n)
        Error("out of bounds");
    if (k == L->n)
        return L->header->left->element;
    p = L->header->right; // 表首结点
    while (i < k)
    {
        p = p->right;
        i++;
    }
    return p->element;
} // O(k)

ListLocate(x,L)功能： 从表中第一个元素开始逐个向后进行线性扫描直到找到表中元素x，返回其位置

ListItem ListLocate(ListItem x, List L)
{
    int i = 1;
    link p;
    p = L->header->right;
    L->header->element = x;
    while (p->element != x)
    {
        p = p->right;
        i++;
    }
    return ((p == L->header) ? 0 : i);
} // O(n)

ListInsert(k,x,L)功能：将元素x插入第k个元素之后，注意此时需要修改向前和向后两个方向的指针

同理，ListDelete(k,L)运算也要修改向前和向后两个方向的指针。

void ListInsert(int k, ListItem x, List L)
{
    link p, y;
    int i;
    if (k < 0 || k > L->n)
        Error("out of bounds");
    p = L->header;
    for (i = 1; i <= k; i++)
        p = p->right; // 自表首头结点始找插入位置
    y = NewNode();
    y->element = x;
    y->left = p;
    y->right = p->right;
    p->right->left = y;
    p->right = y;
    L->n++;
}

PrintList()功能：从表首元素开始线性扫描整个链表并输出每个元素

void PrintList (List L)
{
 link p;
 for (p = L->header->right; p!=L->header; p = p->right)
 ItemShow(p->element);
}
//o(n)

数组与指针的结合

表长较为固定时适合用数组实现，但表元素字节数比较庞大时直接用数组实现时表元素移动所需时间较为费时，解决方法为间接寻址法。

间接寻址法

间接寻址法（Indirect addressing）是计算机程序中一种常见的寻址方式，用于访问内存或寄存器中存储的地址值所指向的数据。

在间接寻址法中，操作数本身并不直接包含要访问的数据，而是包含一个地址值，该地址值指向实际存储数据的位置。通过间接寻址，可以间接地访问存储在其他位置的数据。

假设我们有一个存储器（内存）和一个寄存器R。内存中存储了一组数据，每个数据占据一个单元，而每个单元都有一个唯一的地址。

示意图如下所示：

内存地址   存储数据
  100      Data1
  101      Data2
  102      Data3
  103      Data4
  ...      ...

寄存器R的值： 100

在这个示例中，寄存器R的值为100，它存储了一个地址值。通过间接寻址，我们可以访问地址100对应的数据Data1。具体步骤如下：

1. 从寄存器R中读取地址值100。
2. 使用地址值100，在内存中找到对应的数据Data1。
3. 对Data1进行操作或使用。

伪代码

ListEmpty(L)
功能：测试表是否为空

int ListEmpty(List L)
{ return (L->n==0); }
//O(1) 

ListLength(L)
功能：返回表的长度

int ListLength(List L)
{ return L->n; }
//O(1)

ListRetrieve(k,x)
功能：直接读取table数组第k-1个数组单元中指针所
指向的元素

ListItem ListRetrieve(int k, List L)
{ /*判断k值是否合理，若不合理，返回错误信息*/
 if (k<1 || k>L->n) Error (“out of bounds”);
 //k的取值为1<=k<=n
 return *L->table[k-1];
}
//O(1)

ListLocate(x,L)

功能：在table数组中从前往后依次取出指针所指的表元素和x比较，直到找到一个与x相等的数据元素，则返回它在数组中的存储下标+1；或者查遍整个数组都没有找到与 x 相等的元素，返回0

int ListLocate (LISTItem x, List L)
{ int i;
 for (i=0; i< L->n; i++)
 if (*L->table[i]==x) return ++i; 
 return 0;
}
//假设x存在于第i个位置，则找到x需要比较i次。若x不存在于表L中，则需要进行n次比较。最坏情况下，时间性能为O(n)

ListInsert(k,x,L) 功能：在table数组中将n～k+1处的元素指针分别后移到n+1～k+2，为新的元素指针让出位置

void ListInsert (int k, ListItem x, List L) 
{ int i;
 if (k<0||k>L->n) Error (“out of bounds”);
 if (L->n==L->maxsize) Error (“out of memory”);
 for (i=L->n-1;i>=k;i--) 
 L->table[i+1]=L->table[i]; //指针后移
 L->table[k]=NewNode();
 *L->table[k]=x; 
 L->n++; 
} 

ListDelete(k,L)功能：在table数组中将k+1～n处的元素指针分别前移到k～n-1

ListItem ListDelete (int k, List L) 
{ int i; ListItem x;
 addr p;
 if (k<1||k>L->n) Error (“out of bounds”);
 p= L->table[k-1];
 x=*p;
 for (i=k;i<L->n;i>=k;i++) 
 L->table[i-1]=L->table[i]; //指针前移
 L->n--; 
 free(p); 
 return x; 
}

PrintList(L) 打印链表

 void PrintList(List L)
 {
 int i;
 for (i=0; i<L->n; i++)
 ItemShow(*L->table[i]);
 }

总结如下：

优点 
随机存取表中任一位置的元素（继承数组实现的优点） 
修改指针而非实际移动表中元素以修改表中元素之间的逻辑关系（在每个元素占用空间比较大的时候，优势比较明显）
（继承指针实现的优点） 

缺点 
仍然增加了额外的存储空间（继承指针实现的缺点） 
数组的大小仍然需要预先估计（继承数组实现的缺点） 

适用情况：表长较为固定，但表元素所需字节比较大，间接寻址下指针移动所需时间小于直接用数组实现时表元素移动所需时间

游标表示法

数组与指针结合的另一种方法是：表的游标表示法。游标指的是数组中指示数组单元地址的下标值。

该方法的基本思想：用游标来模拟指针的方法 、数组和指针相结合，这样只需要修改游标不需要移动表中元素，就可以完成插入和删除运算。

伪代码

ListLength(L) 功能：沿着游标线性扫描表，计算长度

int ListLength(List L)
{ int i,len=0;
 i=L->first; //当前表结点游标
 while(i!=-1){
 len++;
 i=L->s->node[i].next;
 }
 return len;
}

ListRetrieve(k,x) 功能：沿着游标线性扫描表，直至找到第k个元素

ListItem ListRetrieve(int k, List L)
{ int p,i=1;
 if (k<1) Error("out of bounds");
 p=L->first;
 while (i<k && p!=-1){
 p=L->s->node[p].next;
 i++;
 }
 return L->s->node[p].element;
 }

ListLocate(x,L) 功能：沿着游标线性扫描表，直至找到元素x，返回其位置

int ListLocate(ListItem x, List L)
{ int p,i=1;
 p=L->first;
 while (p!=-1&&L->s->node[p].element!=x){
 p=L->s->node[p].next;
 i++;
 }
 return ((p>=0)?i:0);
}
//o(n)

ListInsert(k,x,L) 功能：沿着游标线性扫描表，直至找到第k个元素，即找到插入位置

void LsitInsert(int k, ListItem x, List L)
{ int p, y,i;
 if (k < 0) Error("out of bounds");
 p = L->first; 
 for ( i= 1; i < k && p!=-1; i++) 
 p =L->s->node[p].next; //自表首开始找插⼊位置
 y =SpaceAllocate(L->s );
 L->s->node[y]. element = x;
 if (k)
 { L->s->node[y]. next = L->s->node[p]. next; 
 L->s->node[p]. next = y; } // 在位置p处插⼊
 else 
 { L->s->node[y]. next = L->first; 
 L->first = y; } //未使用哨兵结点，在表首插⼊需要特殊处理
}

ListDelete(k,L) 功能：沿着游标线性扫描表，直至找到第k-1个元素，即找到删除位置

将删除元素所在数组单元释放到可用数组空间S中备用（第二个可用空间表）

ListItem ListDelete(int k, List L)
{ int p, q; ListItem x; int i;
 if (k < 1 || ! L->first==-1) Error("out of bounds");
 p = L->first;
 if (k == 1) 
 L->first = L->s->node[p]. next; // 删除表首元素特殊处理
 else {
 q =p; //自表首始找表中第k-1个元素所在结点q
 for (i=1; i<k-1&&q!=-1; i++) q= L->s->node[q]. next; 
 p = L->s->node[q]. next; //让p指向 第k个元素所在结点
 L->s->node[q]. next = L->s->node[p]. next;} // 删除结点p
 x = L->s->node[p]. element; // 第k个元素存⼊x并释放结点p
 SpaceDeallocate(p,L->s);
 return x;
 }

PrintList() 功能：打印表

void PrintList(List L) 
{
 int p;
 for (p=L->first; p!=-1; p=L->s->node[p].next)
 ItemShow(L->s->node[p].element;
}

总结如下：

优点 
可实现多个同类的表共享同一片连续存储空间，给用户予资源
调济的自主权 

缺点 
需要向操作系统申请多大的连续存储空间取决于具体的应用，不容易把握 

适用情形 
存在在多个同类型的表，且相互间存储状态呈现此消彼长的情况 
如果按照表长的极值情况为每张表开辟空间，空间比较浪费