计算机中的进制转换

十进制转二进制

方法一：采用"除2取余，逆序排列"。用十进制整数除2，可以得到一个商和余数；再用商去除2，又会得到一个商和余数，如此进行，直到商为零时为止，然后把先得到的余数作为二进制数的低位有效位，后得到的余数作为二进制数的高位有效位，依次逆序排列起来组合成二进制数。

  例：把(17)10转换为二进制数。

如上图所示17的十进制转换成二进制则是 10001

方法二：采用减法顺排法
十转二采用与相位相减的方法,也是先把2的次方依次排列出来，然后用十进制数与其作对比，比其大或是相等就在相位下写入1，再与其相减，相减后的数再依次与前面作对比，如此进行，比其小就写入0，直至计算到2的0次方。最后从左往右排列出二进制数
下面的表格是8位二进制所对应的十进制数值，对进制转换以及类似题目的理解非常有用

这边注意B代表二进制：D代表十进制

例题： 17D = ______ B

有了上面二进制对应十进制数值的表格，我们就可以将题目给的十进制17拆分为：16+1，再从表格中找到对应的数值，拼凑即可得到答案。
17D = 16D + 1D = 10001B

二进制转十进制

方法一：二进制转为十进制要从右到左用二进制的每个数去乘以2的相应次方（次方从0开始），再将其每个数进行相加
例如1011二进制转十进制

方法二：先把2的次方依次排列出来，再将二进制数倒序依次排列，最后再把对应1的相加起来，0不加 如下图：
例如1011二进制转十进制

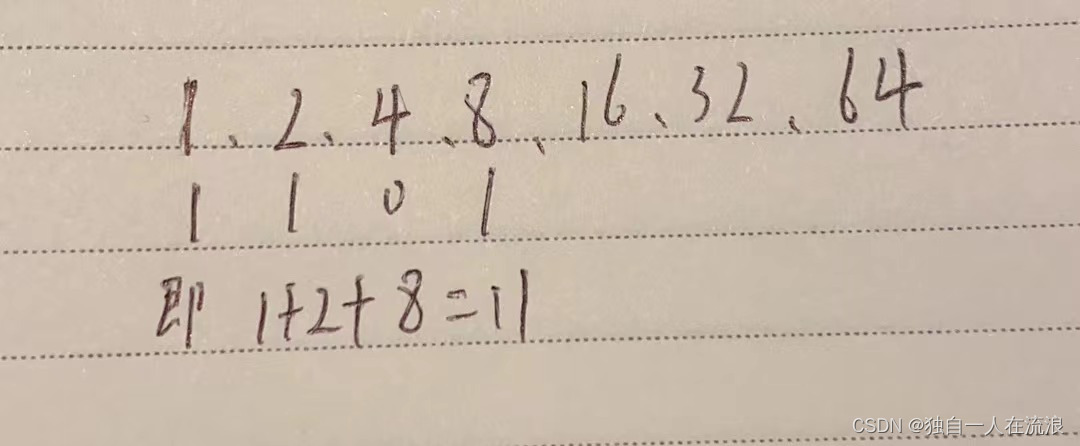
二进制转八进制

拿二进制数10010110举例

首先需要3个二进制数各划分一个区域，不足时则补零。我们可以看出该二进制数为八位，我们需要补充一位，

即010 010 110

从左到右依次是：（计算方法是从右向左依次乘上2的n次幂，n从零开始,^符号表示次幂） 如图

然后合并得到226就是转换后的八进制数。

二进制转16进制

拿二进制数10010110举例

二转16进制与转8进制同理不过是需要4个二进制数各划分一个区域，不足时则补零。我们可以看出该二进制数为八位则不需要补0

即1001 0110 如图

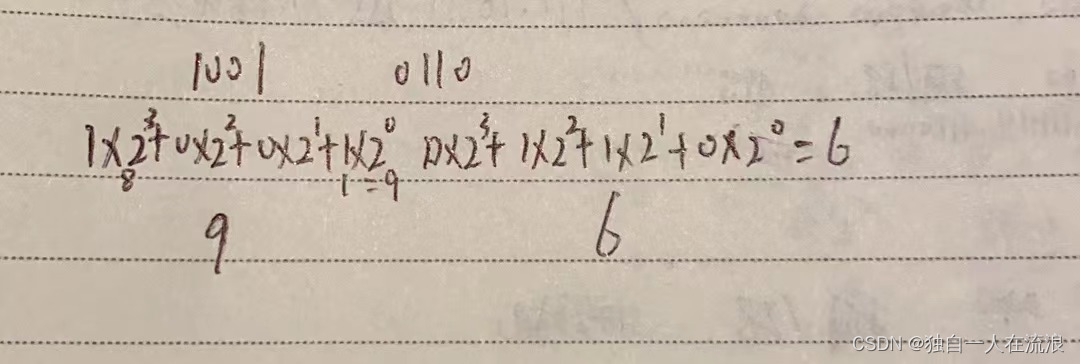
然后合并成96H就是转换后的16进制数

不同数字后面的后缀不同，也代表着不同的数字，比如10D：表示这个数是十进制，10B：表示这个数是二进制，10O：表示这个数是八进制，10H：表示这个数是十六进制。