最小伤害路径算法：迷宫中的深度优先搜索与二分法应用,-优快云博客

本文链接：https://blog.youkuaiyun.com/2301_76805639/article/details/136819181

题目描述

某组织正在策划一起对某大使的刺杀行动。他们来到了使馆，准备完成此次刺杀，要进入使馆首先必须通过使馆前的防御迷阵。

迷阵由 $n\times m$ 个相同的小房间组成，每个房间与相邻四个房间之间有门可通行。在第 $n$ 行的 $m$ 个房间里有 $m$ 个机关，这些机关必须全部打开才可以进入大使馆。而第 $1$ 行的 $m$ 个房间有 $m$ 扇向外打开的门，是迷阵的入口。除了第 11 行和第 $n$ 行的房间外，每个房间都被使馆的安保人员安装了激光杀伤装置，将会对进入房间的人造成一定的伤害。第 $i$ 行第 $j$ 列造成的伤害值为 $p_{i,j}$ （第 $1$ 行和第 $n$ 行的 $p$ 值全部为 $0$ ）。

现在某组织打算以最小伤害代价进入迷阵，打开全部机关，显然，他们可以选择任意多的人从任意的门进入，但必须到达第 $n$ 行的每个房间。一个士兵受到的伤害值为他到达某个机关的路径上所有房间的伤害值中的最大值，整个部队受到的伤害值为所有士兵的伤害值中的最大值。现在，这个恐怖组织掌握了迷阵的情况，他们需要提前知道怎么安排士兵的行进路线可以使得整个部队的伤害值最小。

输入格式

第一行有两个整数 $n,m$ ，表示迷阵的大小。

接下来 $n$ 行，每行 $m$ 个数，第 $i$ 行第 $j$ 列的数表示 $p_{i,j}$ 。

输出格式

输出一个数，表示最小伤害代价。

输入输出样例

输入

输出

说明/提示

$50$ %的数据， $n,m\leqslant100$
$100$ %的数据， $n,m\leqslant 1000 , p_{i,j}\leqslant 1000$ 。

题意概括

找一条路径,使得从第 $1$ 行到第 $n$ 行路径的最大值最小。

样例解释

我们先建一个图

根据题目中边权为两点权中最大值得出带权图

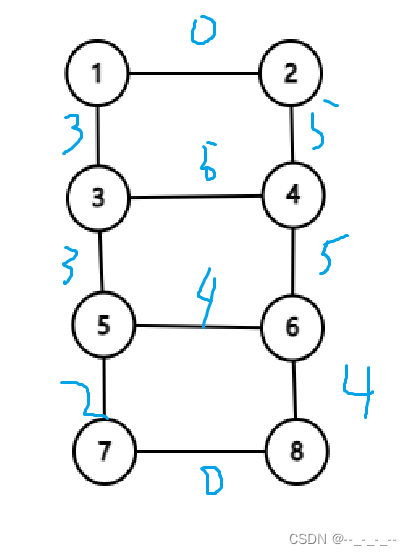
因此可以想到答案为

分析

根据样例以及题目概括，我们可以用二分与搜索

求最大值最小，可以二分答案求解——规定一个限制，如果边权大于限制则不走这条路。若一直大于只能用更大的值限制。

but漏洞：

我们限制最大伤害为5

搜索到某一行发现伤害值是这样的 ——>8 8 8 。

按上这样我们是无法通过这一行的。

所以我们需要标记是否能以当前限制的伤害值走到最后一行,如果可以我们就去寻求更小伤害,如果不能我们只能去寻求较小伤害(实际上是更大了)。

二分：

int l=0,r=1008;
//这里右边界赋为了极大值
//数据保证了每个位置伤害值不超过1000
//也可以把右边界赋值为当前图中最大伤害值.
while(l<=r) { //一般套路
	int mid=(l+r)/2;
	memset(vis,0,sizeof vis);
	flg=0;
	dfs(1,1,mid);
	if(flg==1)//flg为1视为能到达最后一行
		r=mid-1;//因此我们更新右边界,寻求更小值
	else l=mid+1;
}

如何搜索：

需要判断:是否超出边界,是否遍历过,伤害值是否能满足限制条件就可以.


const int dx[]= {0,1,0,-1}; //偏移量
const int dy[]= {1,0,-1,0};
void dfs(int x,int y,int mid) {
	if(x==n) {
		flg=1;
		return;
	}
	vis[x][y]=1;
	for(int i=0; i<4; ++i) {
		int xx=x+dx[i],yy=y+dy[i];
		//限定范围||大小不超过限制||步数 
		if(xx<1 || xx>n || yy<1 || yy>m || vis[xx][yy] || p[xx][yy]>mid) continue;
		dfs(xx,yy,mid);
		if(flg) return;
	}
}

代码

真就是纯搜索而已

#include<bits/stdc++.h>
using namespace std;
typedef int intt;
#define int long long
#define F(a,b,c) for(int a=b;a<=c;a++)
#define maxn 1008
const int dx[]= {0,1,0,-1};
const int dy[]= {1,0,-1,0};
int n,m,a[maxn][maxn];
bool flg,vis[maxn][maxn];
void dfs(int x,int y,int mid) {
	if(x==n) {
		flg=1;
		return;
	}
	vis[x][y]=1;
	for(int i=0; i<4; ++i) {
		int xx=x+dx[i],yy=y+dy[i];
		if(xx<1 || xx>n || yy<1 || yy>m || vis[xx][yy] || a[xx][yy]>mid) continue;
		dfs(xx,yy,mid);
		if(flg) return;
	}
}
intt main() {
	cin>>n>>m;
	for(int i=1; i<=n; i++) {
		for(int j=1; j<=m; j++) {
			cin>>a[i][j];
		}
	}

	int l=0,r=maxn;
//这里右边界赋为了极大值
//数据保证了每个位置伤害值不超过1000
//也可以把右边界赋值为当前图中最大伤害值.
	while(l<=r) { //一般套路
		int mid=(l+r)/2;
		memset(vis,0,sizeof vis);
		flg=0;
		dfs(1,1,mid);
		if(flg==1)//flg为1视为能到达最后一行
			r=mid-1;//因此我们更新右边界,寻求更小值
		else l=mid+1;
	}
	cout<<l;
}