时间序列分析——移动平均法、指数平滑法、逐步回归法、趋势外推法等（基于Python实现）

已于 2024-11-14 18:59:01 修改
阅读量608 收藏 1
点赞数
分类专栏： 统计学——基于Python 文章标签： python
于 2024-11-14 18:44:06 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/2301_76574743/article/details/143778013
版权

第 11章——时间序列分析和预测

【例11-1】 绘制时间序列折线图—观察成分

【代码框11-1】——绘制时间序列折线图

# 图11-2的绘制代码
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
df = pd.read_csv('./pydata/example/chap11/example11_1.csv')

# 绘制折线图
plt.subplots(2, 2, figsize=(8.5, 6.5))
plt.subplot(221)
df['净利润'].plot(kind='line',linewidth=1,marker='o',\
               markersize=4,xlabel='年份',ylabel='净利润')
plt.xticks(range(0, 18, 2), df['年份'][::2])
plt.title('(a) 净利润序列')

plt.subplot(222)
df['产量'].plot(kind='line',linewidth=1,marker='o',\
              markersize=4,xlabel='年份',ylabel='产量')
plt.xticks(range(0, 18, 2), df['年份'][::2])
plt.title('(b) 产量序列')

plt.subplot(223)
df['管理成本'].plot(kind='line',linewidth=1,marker='o',\
                markersize=4,xlabel='年份',ylabel='管理成本')
plt.xticks(range(0, 18, 2), df['年份'][::2])
plt.title('(c) 管理成本序列')

plt.subplot(224)
df['销售价格'].plot(kind='line',linewidth=1,marker='o',\
                markersize=4,xlabel='年份',ylabel='销售价格')
plt.xticks(range(0, 18, 2), df['年份'][::2])
plt.title('(d) 销售价格序列')

plt.tight_layout()   # 紧凑布局

在这里插入图片描述

df.head()#;df.tail()
年份净利润产量管理成本销售价格
020061200.64628.0199
120071750.75660.3233
220082938.16373.5213
320093126.0129121.3230
420103250.3173126.9223

【例11-2】 绘制时间序列折线图

【代码框11-2】——绘制时间序列折线图

# 图11-3的绘制代码
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

# 加载数据
example11_2 = pd.read_csv('./pydata/example/chap11/example11_2.csv')

# 融合数据
df = pd.melt(example11_2, id_vars=['月份'], var_name='年份', value_name='销售量')
df['日期'] = df['年份'] + "-" + df['月份']  # 添加带有年份和月份的日期列
df['日期'] = pd.to_datetime(df['日期'].map(lambda x: x.replace("年", '').replace("月", '')))  # 创建时间序列
df.index = df['日期']  # 将日期设置为索引

plt.subplots(1, 2, figsize=(11, 4.5))

# （a）销售量的折线图
plt.subplot(121)
plt.plot(df['销售量'], marker='o', linewidth=1, markersize=4)
plt.xlabel('时间')
plt.ylabel('销售量')
plt.title("(a) 销售量的折线图", size=15)
for i in range(2019, 2024):
    plt.vlines(pd.to_datetime(str(i) + "-01-01"), 90, 300, linestyles='--', linewidth=0.6, color='grey')

# （b）销售量的按年折叠图
plt.subplot(122)
sns.lineplot(x='月份', y='销售量', hue='年份', data=df, marker='o', markersize=5, linewidth=1)
plt.title("(b) 销售量的按年折叠图", size=15)

plt.tight_layout()  # 紧凑布局
plt.show()

# （c）销售量的按月箱形图
# plt.subplot(313)
# sns.boxplot(df['月份'],df['销售量'])
# plt.title("（c）按月箱线图")

plt.tight_layout()   # 紧凑布局

在这里插入图片描述

<Figure size 640x480 with 0 Axes>

【例11-3】 成分分解

【代码框11-3】——饮料销售量的成分分解

# 序列成分分解（使用代码框11-2创建的时间序列df）
import pandas as pd 
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose
plt.rcParams['font.sans-serif']=['SimHei']
example11_2 = pd.read_csv('./pydata/example/chap11/example11_2.csv')

df = pd.melt(example11_2,id_vars=['月份'],var_name='年份',value_name='销售量')# 融合数据
df['日期'] = df['年份']+"-"+df['月份']  # 添加带有年份和月份的日期列
df['日期'] = pd.to_datetime(df['日期'].map(lambda x : x.replace("年",'').replace("月",''))) 
                                                             # 创建时间序列
df.index=df['日期']  # 将日期设置为索引

# 销售量的成分分解（采用乘法模型）
sale_compose = seasonal_decompose(df['销售量'],
                                  model='multiplicative',    # 采用乘法模型分解
                                  period=12,                 # 设置序列周期
                                  two_sided=True,            # 默认，使用中心化移动平均
                                  extrapolate_trend='freq')  # 输出趋势成分和随机成分
# 展示各成分的分解结果和观测值
df_sale=pd.concat([sale_compose.seasonal,          # 季节成分
                   sale_compose.trend,             # 趋势成分
                   sale_compose.resid,             # 随机成分
                   sale_compose.observed],axis=1)  # 观测值
round(df_sale,4)     # 展示结果的前5行和后5行
seasonaltrendresid销售量
日期
2018-01-010.8967125.87561.0295116.2
2018-02-010.8488127.75871.0309111.8
2018-03-010.9828129.64181.0062128.2
2018-04-010.9571131.52491.0256129.1
2018-05-010.9826133.40800.9887129.6
...............
2023-08-011.2541232.62180.9961290.6
2023-09-011.0645234.71361.0134253.2
2023-10-010.9207236.80541.0086219.9
2023-11-010.8049238.89721.0401200.0
2023-12-010.8983240.98901.0629230.1

72 rows × 4 columns

# 绘制成分分解图（图11-4）
#plt.rcParams.update({'figure.figsize':(6,10)})# 设置图形大小
#sale_compose.plot()  # 绘制成分分解图

fig = sale_compose.plot()  # 绘制成分分解图
fig.set_size_inches(6,8)  # 设置图形大小
plt.tight_layout()   # 紧凑布局

在这里插入图片描述

函数默认model=‘additive’，即采用加法模型进行分解

运行sale_compose.seasonal[0:12] 可得12个月的季节指数

sale_compose.seasonal[0:12].plot(marker=‘o’)# 绘制季节指数图

?sale_compose.plot

【例11-4】 移动平均平滑

【代码框11-4】——销售价格的移动平均平滑

import pandas as pd
df = pd.read_csv('./pydata/example/chap11/example11_1.csv')

# 移动平均法绘制时间序列图
ma3 = df['销售价格'].rolling(window=3, center=True).mean() # 3期移动平均
ma5 = df['销售价格'].rolling(window=5, center=True).mean() # 5期移动平均
df_ma = pd.DataFrame({"年份":df['年份'],"销售价格": df['销售价格'],
                      "3期移动平均": ma3, "5期移动平均": ma5})
round(df_ma,2).head()  # 显示前5行规
年份销售价格3期移动平均5期移动平均
02006199NaNNaN
12007233215.00NaN
22008213225.33219.6
32009230222.00227.8
42010223231.00222.8
# 绘制实际值和平滑值的折线图（图11-5）
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']

plt.figure(figsize=(8,5.5))
l1,= plt.plot(df_ma['销售价格'],linestyle='-', marker='o',linewidth=0.8)
l2,= plt.plot(df_ma['3期移动平均'],linestyle='-.', marker='+',linewidth=0.8)
l3,= plt.plot(df_ma['5期移动平均'],linestyle='-.', marker='*',linewidth=0.8)
plt.xticks(range(0, 18, 2), df['年份'][::2])
plt.legend(handles=[l1,l2,l3],labels=['销售价格','3 期移动平均','5 期移动平均'],
           loc='best',prop={'size': 10})
plt.xlabel('时间',size=12)
plt.ylabel("销售价格",size=12)

Text(0, 0.5, '销售价格')

在这里插入图片描述

# 11.3 指数平滑预测

【例11-5】——销售价格的简单指数平滑预测

【代码框11-5】——销售价格的简单指数平滑预测

import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.holtwinters import SimpleExpSmoothing
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
df = pd.read_csv('./pydata/example/chap11/example11_1.csv')

df.index= pd.date_range(start='2006', end='2023', freq='AS') 
                                           # 返回从1月1日开始的固定频率的日期时间索引

# 拟合简单指数平滑模型(alpha=0.3)
model = SimpleExpSmoothing(df['销售价格']).fit(smoothing_level=0.3, optimized=True)
model.params     # 输出模型参数

C:\Users\VICTUS\AppData\Local\Temp\ipykernel_9600\2524019978.py:8: FutureWarning: 'AS' is deprecated and will be removed in a future version, please use 'YS' instead.
  df.index= pd.date_range(start='2006', end='2023', freq='AS')
D:\python\Lib\site-packages\pandas\util\_decorators.py:213: EstimationWarning: Model has no free parameters to estimate. Set optimized=False to suppress this warning
  return func(*args, **kwargs)





{'smoothing_level': 0.3,
 'smoothing_trend': nan,
 'smoothing_seasonal': nan,
 'damping_trend': nan,
 'initial_level': 199.0,
 'initial_trend': nan,
 'initial_seasons': array([], dtype=float64),
 'use_boxcox': False,
 'lamda': None,
 'remove_bias': False}

# 绘制实际值和拟合值图（图11-6）
df['price_ses'] = model.fittedvalues
plt.figure(figsize=(7,4.5))
l1, = plt.plot(df['销售价格'],linestyle='-', marker='o',linewidth=0.8)
l2, = plt.plot(df['price_ses'],linestyle='--', marker='*',linewidth=0.8)
plt.legend(handles=[l1,l2],labels=['销售价格','拟合值'],loc='best',prop={'size': 10})
plt.xlabel('时间',size=12)
plt.ylabel("销售价格",size=12)

Text(0, 0.5, '销售价格')

在这里插入图片描述

# 计算2024年的预测值
p_model = model.forecast(1)  # 向后预测1期
p_model

2024-01-01    221.460406
Freq: YS-JAN, dtype: float64

# 绘制预测图和残差图（图11-7）
import scipy

# 图（a）预测图
plt.subplots(1, 2, figsize=(11, 4))
plt.subplot(121)

ax = df['销售价格'].plot(marker="o",linewidth=0.8,color="black")     # 绘制实际值
ax.set_ylabel("销售价格",size=12)
ax.set_xlabel("时间",size=12)
model.forecast(1).plot(ax=ax, style="--", marker="o", color="red")  # 绘制预测值
simulations = model.simulate(nsimulations=2, repetitions=1000, 
                             error="add",random_errors=scipy.stats.norm)   
                                 # 重复模拟100次，模拟步长为2；random_errors="bootstrap"
# 计算置信区间并绘图
low_CI_95 = p_model-1.96*simulations.std(axis=1)
high_CI_95 = p_model+1.96*simulations.std(axis=1)
low_CI_80 = p_model-1.28*simulations.std(axis=1)
high_CI_80 = p_model+1.28*simulations.std(axis=1)

plt.fill_between(['2024'],low_CI_95,high_CI_95,alpha=0.3,color='grey',linewidth=20)
plt.fill_between(['2024'],low_CI_80,high_CI_80,alpha=0.3,color='blue',linewidth=20)
plt.xlim('2005','2025')
plt.title('(a) 销售价格的简单指数平滑预测',size=13)

# 图（b）残差图
res = model.resid
plt.subplot(122)
plt.scatter(range(len(res)),res, marker='o')
plt.hlines(0,0,17,linestyle='--',color='red')
plt.xticks(range(0, 18, 2), df['年份'][::2])
plt.xlabel('时间',size=12)
plt.ylabel("残差",size=12)
plt.title('(b) 简单指数平滑预测残差',size=13)

Text(0.5, 1.0, '(b) 简单指数平滑预测残差')

在这里插入图片描述

# 补充——简单指数平滑预测
import pandas as pd
#from statsmodels.tsa.holtwinters import SimpleExpSmoothing
#import matplotlib.pyplot as plt
#plt.rcParams['font.sans-serif']=['SimHei']
#plt.rcParams['axes.unicode_minus']=False  # 用来正常显示负号
df = pd.read_csv('./pydata/chap12/example12_3.csv',encoding='gbk')
#df.index= pd.date_range(start='2006', end='2022', freq='AS')    # 返回从1月1日开始的固定频率的日期时间索引
#df['简单指数平滑预测']=df['销售价格'].ewm(alpha=0.3).mean()

【例11-6】——净利润的Holt指数平滑预测

【代码框11-6】——净利润的Holt指数平滑预测

import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.holtwinters import SimpleExpSmoothing,ExponentialSmoothing,Holt

plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False  # 用来正常显示负号

df = pd.read_csv('./pydata/example/chap11/example11_1.csv')
df.index=pd.date_range(start="2006", end="2023", freq="AS")

# 拟合Holt指数平滑模型(model_h)
model_h = Holt(df['净利润']).fit(optimized=True)
model_h.params     # 输出模型系数


C:\Users\VICTUS\AppData\Local\Temp\ipykernel_9600\3727735978.py:9: FutureWarning: 'AS' is deprecated and will be removed in a future version, please use 'YS' instead.
  df.index=pd.date_range(start="2006", end="2023", freq="AS")





{'smoothing_level': 0.33499999999999996,
 'smoothing_trend': 0.33499999999999996,
 'smoothing_seasonal': nan,
 'damping_trend': nan,
 'initial_level': 1200.6,
 'initial_trend': 550.1000000000001,
 'initial_seasons': array([], dtype=float64),
 'use_boxcox': False,
 'lamda': None,
 'remove_bias': False}

# 绘制实际值和拟合值图（图11-8）
df['净利润_holt'] = model_h.fittedvalues
plt.figure(figsize=(7,4.5))
l1, = plt.plot(df['净利润'],linestyle='-', marker='o',linewidth=1)
l2, = plt.plot(df['净利润_holt'],linestyle='--', marker='^',linewidth=1)
plt.legend(handles=[l1,l2],labels=['净利润','拟合值'],loc='best',prop={'size': 10})
plt.xlabel('时间',size=12)
plt.ylabel("净利润",size=12)


Text(0, 0.5, '净利润')

在这里插入图片描述

# 2024净利润的预测
model_h.forecast(1)

2024-01-01    7871.893322
Freq: YS-JAN, dtype: float64

# 绘制预测图和残差图（图11-9）
import scipy

# 图（a）预测图
plt.subplots(1, 2, figsize=(11, 4))
plt.subplot(121)

ax = df['净利润'].plot(marker="o",linewidth=1,color="black")  # 绘制实际值
ax.set_ylabel("净利润",size=12)
ax.set_xlabel("时间",size=12)
model_h.forecast(1).plot(ax=ax, style="--", marker="o", color="red")# 绘制预测值
# 绘制置信区间
simulations = model_h.simulate(2, repetitions=1000, error="add",
                           random_errors=scipy.stats.norm)
low_CI_95 = model_h.forecast(1)-1.96*simulations.std(axis=1)
high_CI_95 = model_h.forecast(1)+1.96*simulations.std(axis=1)
low_CI_80 = model_h.forecast(1)-1.28*simulations.std(axis=1)
high_CI_80 = model_h.forecast(1)+1.28*simulations.std(axis=1)

plt.fill_between(['2024'],low_CI_95,high_CI_95,alpha=0.3,color='grey',linewidth=20)
plt.fill_between(['2024'],low_CI_80,high_CI_80,alpha=0.3,color='blue',linewidth=20)
plt.xlim('2005','2025')
plt.title('(a) 净利润的Holt指数平滑预测',size=13)

# 图（b）残差图
plt.subplot(122)
res = model_h.resid
plt.scatter(range(len(res)),res, marker='o')
plt.hlines(0,0,17,linestyle='--',linewidth=1,color='red')
plt.xlabel('时间',size=12)
plt.xticks(range(0, 18, 2), df['年份'][::2])
plt.ylabel("残差",size=12)
plt.title('(b) Holt指数平滑预测残差',size=13)

plt.show()

在这里插入图片描述

【例11-7】——饮料销售量的Winters指数平滑预测

【代码框11-7】——饮料销售量的Winters指数平滑预测

import pandas as pd 
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from statsmodels.tsa.holtwinters import SimpleExpSmoothing,ExponentialSmoothing,Holt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
df = pd.read_csv('./pydata/example/chap11/example11_2.csv')

df = pd.melt(df,id_vars=['月份'],var_name='年份',value_name='销售量')
df['日期'] = df['年份']+"-"+df['月份']
df['日期'] = pd.to_datetime(df['日期'].map(lambda x : x.replace("年",'').replace("月",'')))

#  拟合Winters模型（(model_w)），并确定模型参数α，β和γ以及模型系数a，b和s
model_w = ExponentialSmoothing(df['销售量'], 
                                    trend="add",
                                    seasonal="add",seasonal_periods=12,
                                    initialization_method="estimated",).fit()
model_w.params


{'smoothing_level': 0.26747342753802866,
 'smoothing_trend': 0.0,
 'smoothing_seasonal': 0.7325265724619714,
 'damping_trend': nan,
 'initial_level': 125.54947674056427,
 'initial_trend': 1.7032392870942314,
 'initial_seasons': array([-11.05258326, -15.44428272,   0.80581954,   0.11696509,
         -0.25575943,  19.38978389,  38.33927594,  26.48675657,
          4.15733834, -17.23933032, -36.32966176, -18.17728823]),
 'use_boxcox': False,
 'lamda': None,
 'remove_bias': False}

# Winters模型的拟合图（图11-10）
df['销售量_hw'] = model_w.fittedvalues
plt.figure(figsize=(7,4.5))
l1, = plt.plot(df['日期'],df['销售量'],linestyle='-', marker='o',linewidth=1,markersize=4)
l2, = plt.plot(df['日期'],df['销售量_hw'],linestyle='--', marker='*',linewidth=1,markersize=4)
plt.legend(handles=[l1,l2],labels=['销售量','拟合值'],loc='best',prop={'size': 10})
plt.xlabel('时间',size=12)
plt.ylabel("销售量",size=12)

Text(0, 0.5, '销售量')

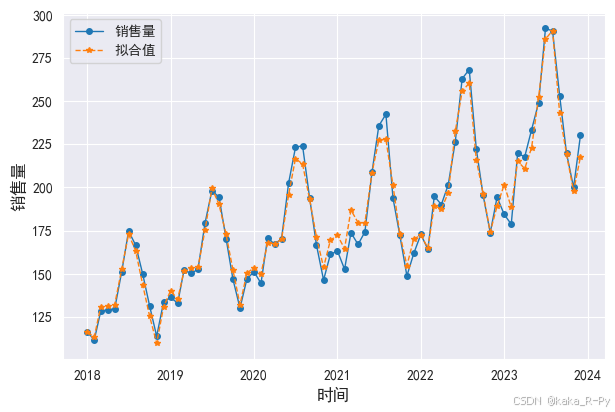
在这里插入图片描述

# Winters 模型2024年销售量的预测
model_w1 = model_w.forecast(12)
round(model_w1,4)   #  np.array(model_w1)

72    215.5819
73    212.5197
74    252.3115
75    248.5671
76    261.3794
77    278.0306
78    319.3686
79    317.8368
80    277.7175
81    244.2291
82    223.7609
83    241.4409
dtype: float64

# 绘制预测图和残差图（图11-11）
import scipy

# 图（a）预测图
plt.subplots(1, 2, figsize=(11, 4))
plt.subplot(121)

ax = df['销售量'].plot(marker="o",markersize=4,linewidth=1,color="black")# 绘制实际值
ax.set_ylabel("销售量",size=12)
ax.set_xlabel("时间",size=12)
# 绘制2024年12个月的预测值
model_w.forecast(12).plot(ax=ax, style="--", marker="o",linewidth=1, markersize=4,color="red")
plt.xticks(range(0, 72, 12), df['年份'][::12])
plt.axvline(72, ls='--', c='grey',linewidth=1)
plt.title('(a) 销售量的Winters指数平滑预测',size=13)

# 图（b）残差图
plt.subplot(122)
res = model_w.resid
plt.scatter(range(len(res)),res, marker='^')
plt.hlines(0,0,72,linestyle='--',linewidth=1,color='red')
plt.xlabel('时间',size=12)
plt.ylabel("残差",size=12)
plt.xticks(range(0, 72, 12), df['年份'][::12])
plt.title('(b) Winters指数平滑预测残差',size=13)

plt.show()

在这里插入图片描述

# 11.4 趋势外推预测

【例11-8】——净利润的一元线性回归预测

【代码框11-8】——净利润的一元线性回归预测

import pandas as pd
from statsmodels.formula.api import ols
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
df = pd.read_csv('./pydata/example/chap11/example11_1.csv')

# 拟合一元线性回归模型（l_model）
l_model = ols("净利润~年份",data=df).fit()
print(l_model.summary())  # 输出模型结果

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                    净利润   R-squared:                       0.952
Model:                            OLS   Adj. R-squared:                  0.949
Method:                 Least Squares   F-statistic:                     314.7
Date:                Thu, 14 Nov 2024   Prob (F-statistic):           6.03e-12
Time:                        17:47:21   Log-Likelihood:                -134.04
No. Observations:                  18   AIC:                             272.1
Df Residuals:                      16   BIC:                             273.9
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept  -7.092e+05   4.03e+04    -17.617      0.000   -7.95e+05   -6.24e+05
年份           354.5140     19.985     17.739      0.000     312.148     396.880
==============================================================================
Omnibus:                        0.082   Durbin-Watson:                   1.812
Prob(Omnibus):                  0.960   Jarque-Bera (JB):                0.306
Skew:                           0.051   Prob(JB):                        0.858
Kurtosis:                       2.369   Cond. No.                     7.82e+05
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 7.82e+05. This might indicate that there are
strong multicollinearity or other numerical problems.


D:\python\Lib\site-packages\scipy\stats\_stats_py.py:1806: UserWarning: kurtosistest only valid for n>=20 ... continuing anyway, n=18
  warnings.warn("kurtosistest only valid for n>=20 ... continuing "

# 计算各年的预测值和预测残差
df_pre = pd.DataFrame({"年份": df['年份'], "净利润": df['净利润'], 
                       "预测值": l_model.fittedvalues, "预测残差": l_model.resid})
df_pre.loc[18, '年份'] = 2024
df_pre = df_pre.astype({'年份': int})  # 年份为整数
df_pre.loc[18, '预测值'] = l_model.predict(exog=dict(年份=2024)).values # 2024年的预测值

round(df_pre,2).head()
年份净利润预测值预测残差
020061200.61919.55-718.95
120071750.72274.06-523.36
220082938.12628.58309.52
320093126.02983.09142.91
420103250.33337.60-87.30
# 绘制预测图和残差图（图11-12）
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 图（a）预测图
plt.subplots(1, 2, figsize=(11, 4))
plt.subplot(121)
l1=plt.plot(df_pre['净利润'], marker='o')
l2=plt.plot(df_pre['预测值'], marker='*',linewidth=1,markersize=8,ls='-.')
plt.axvline(17, ls='--', c='grey',linewidth=1)
plt.xticks(range(0, 19, 2), df_pre['年份'][::2])
plt.xlabel('年份',size=12)
plt.ylabel('净利润',size=12)
plt.legend(['净利润', '预测值'],prop={'size': 11})
plt.title('(a) 净利润的一元线性回归预测',size=13)

# 图（b）残差图
plt.subplot(122)
res = l_model.resid  # 计算残差
plt.scatter(range(len(res)),res, marker='o',linewidth=1)
plt.hlines(0,0,17,linestyle='--',color='red',linewidth=1)
plt.xlabel('时间',size=12)
plt.xticks(range(0, 19, 2), df_pre['年份'][::2])
plt.ylabel("残差",size=12)
plt.title('(b) 一元线性回归预测残差',size=13)

plt.show()

在这里插入图片描述

【例11-9】——产量的指数曲线预测

【代码框11-9】——产量的指数曲线预测

import pandas as pd
import numpy as np
from statsmodels.formula.api import ols
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
df = pd.read_csv('./pydata/example/chap11/example11_1.csv')

# 拟合指数曲线模型（e_model）
e_model = ols("np.log(产量)~年份",data=df).fit()
print(e_model.summary())   # 输出模型结果


                            OLS Regression Results                            
==============================================================================
Dep. Variable:             np.log(产量)   R-squared:                       0.993
Model:                            OLS   Adj. R-squared:                  0.992
Method:                 Least Squares   F-statistic:                     2184.
Date:                Thu, 14 Nov 2024   Prob (F-statistic):           1.54e-18
Time:                        17:47:33   Log-Likelihood:                 11.497
No. Observations:                  18   AIC:                            -18.99
Df Residuals:                      16   BIC:                            -17.21
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept   -573.2192     12.401    -46.224      0.000    -599.508    -546.930
年份             0.2877      0.006     46.733      0.000       0.275       0.301
==============================================================================
Omnibus:                        0.827   Durbin-Watson:                   1.471
Prob(Omnibus):                  0.661   Jarque-Bera (JB):                0.552
Skew:                          -0.406   Prob(JB):                        0.759
Kurtosis:                       2.720   Cond. No.                     7.82e+05
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 7.82e+05. This might indicate that there are
strong multicollinearity or other numerical problems.


D:\python\Lib\site-packages\scipy\stats\_stats_py.py:1806: UserWarning: kurtosistest only valid for n>=20 ... continuing anyway, n=18
  warnings.warn("kurtosistest only valid for n>=20 ... continuing "

# 计算各年的预测值和预测残差
df_pre = pd.DataFrame({"年份": df['年份'], "产量": df['产量'],
                       "预测值": np.exp(e_model.fittedvalues)})
df_pre['残差'] = df_pre['产量'] - df_pre['预测值']
df_pre.loc[18, '年份'] = 2024
df_pre = df_pre.astype({'年份': int})
df_pre.loc[18, '预测值'] = np.exp(e_model.predict(exog=dict(年份=2024)).values)

round(df_pre,2).head()
年份产量预测值残差
0200646.048.13-2.13
1200756.064.17-8.17
2200863.085.56-22.56
32009129.0114.0814.92
42010173.0152.1120.89
# 绘制预测图和残差图（图11-13）
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus']=False

# 图（a）预测图
plt.subplots(1, 2, figsize=(11, 4))
plt.subplot(121)

l1=plt.plot(df_pre['产量'], marker='o',linewidth=1)
l2=plt.plot(df_pre['预测值'], marker='*',markersize=6,linewidth=1,ls='-.')
plt.axvline(17, ls='--', c='grey',linewidth=1)
plt.xticks(range(0, 19, 2), df_pre['年份'][::2])
plt.xlabel('年份',size=12)
plt.ylabel('产量',size=12)
plt.legend(['产量', '预测值'],prop={'size': 11})
plt.title('(a) 产量的指数曲线预测',size=13)

# 图（b）残差图
plt.subplot(122)
df_pre['残差'] = df_pre['产量'] - df_pre['预测值']
plt.scatter(range(len(df_pre['残差'])),df_pre['残差'], marker='o')
plt.hlines(0,0,17,linestyle='--',linewidth=1,color='red')
plt.xlabel('时间',size=12)
plt.xticks(range(0, 19, 2), df_pre['年份'][::2])
plt.ylabel("残差",size=12)
plt.title('(b) 指数曲线预测残差',size=13)

plt.show()

在这里插入图片描述

【例11-10】管理成本的二阶曲线和三阶曲线预测

【代码框11-10】——管理成本的二阶曲线和三阶曲线预测

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from statsmodels.formula.api import ols
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
df = pd.read_csv('./pydata/example/chap11/example11_1.csv')

# 拟合二阶曲线模型（model2）和三阶曲线模型（model3）
df['t'] = df['年份']-2005
model2 = ols("管理成本~t+pow(t,2)",data=df).fit()           # 拟合二阶曲线
model3 = ols("管理成本~t+pow(t,2)+pow(t,3)",data=df).fit()  # 拟合三阶曲线

# 计算二阶曲线和三阶曲线的预测值和残差
df_pre = pd.DataFrame({"年份": df['年份'], "管理成本": df['管理成本'],
                       "二阶曲线预测值": model2.fittedvalues,"二阶曲线残差": model2.resid,
                       "三阶曲线预测值": model3.fittedvalues,"三阶曲线残差": model3.resid})

df_pre.loc[18, '年份'] = 2024
df_pre = df_pre.astype({'年份': int})
df_pre.loc[18, '二阶曲线预测值'] = model2.predict(exog=dict(t=19)).values
df_pre.loc[18, '三阶曲线预测值'] = model3.predict(exog=dict(t=19)).values
round(df_pre,2)
年份管理成本二阶曲线预测值二阶曲线残差三阶曲线预测值三阶曲线残差
0200628.029.07-1.072.6025.40
1200760.363.07-2.7755.295.01
2200873.593.93-20.4398.99-25.49
32009121.3121.65-0.35134.50-13.20
42010126.9146.23-19.33162.58-35.68
52011172.4167.664.74184.01-11.61
62012218.7185.9632.74199.5819.12
72013227.7201.1126.59210.0617.64
82014254.6213.1241.48216.2338.37
92015224.0221.982.02218.875.13
102016226.5227.71-1.21218.767.74
112017232.0230.301.70216.6715.33
122018200.1229.74-29.64213.39-13.29
132019181.8226.04-44.24209.69-27.89
142020173.8219.20-45.40206.35-32.55
152021210.2209.220.98204.166.04
162022206.5196.0910.41203.882.62
172023223.6179.8343.77206.3017.30
182024NaN160.42NaN212.19NaN
# 实际值和预测值曲线（图11-14）
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus']=False

# 图（a）预测图
plt.subplots(1, 2, figsize=(11, 4))
plt.subplot(121)
l1=plt.plot(df_pre['管理成本'], marker='o',linewidth=1)
l2=plt.plot(df_pre['二阶曲线预测值'], marker='+', ls='-.',linewidth=1)
l3=plt.plot(df_pre['三阶曲线预测值'], marker='*', ls='-.',linewidth=1)

plt.axvline(16, ls='--', c='grey',linewidth=1)
plt.xticks(range(0, 19, 2), df_pre['年份'][::2])
plt.xlabel('年份',size=12)
plt.ylabel('管理成本',size=12)
plt.legend(['管理成本', '二阶曲线预测值','三阶曲线预测值'],prop={'size': 11})
plt.title('(a) 管理成本的二阶曲线和三阶曲线预测',size=13)

# 图（b）残差图
plt.subplot(122)
plt.scatter(range(len(df_pre['二阶曲线残差'])),df_pre['二阶曲线残差'], marker='+')
plt.scatter(range(len(df_pre['三阶曲线残差'])),df_pre['三阶曲线残差'], marker='*',linewidth=1)
plt.hlines(0,0,18,linestyle='--',color='red',linewidth=1)

plt.xticks(range(0, 19, 2), df_pre['年份'][::2])
plt.xlabel('年份',size=12)
plt.ylabel('残差',size=12)
plt.legend([ '二阶曲线残差','三阶曲线残差'],prop={'size': 11})
plt.title('(b) 二阶曲线和三阶曲线预测残差',size=13)

plt.show()

在这里插入图片描述

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

kaka_R-Py

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值