本科课程参见:《软件学院那些课》
算法原理
对于常微分方程初值问题

在求解区间[a,b]上作等距分割的剖分,步长 ,记
,记 。用数值微商的方法,即用差商近似微商数值求解常微分方程。
。用数值微商的方法,即用差商近似微商数值求解常微分方程。
用向前差商近似
做出y(x)的在x=x0处的一阶向前差商式:

又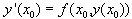 ,于是得到
,于是得到
本科课程参见:《软件学院那些课》
对于常微分方程初值问题

在求解区间[a,b]上作等距分割的剖分,步长 ,记
,记 。用数值微商的方法,即用差商近似微商数值求解常微分方程。
。用数值微商的方法,即用差商近似微商数值求解常微分方程。
用向前差商近似
做出y(x)的在x=x0处的一阶向前差商式:

又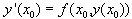 ,于是得到
,于是得到
 1170
1170
 5万+
5万+
 684
684

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


