LM算法在相机标定的应用共有三处。
(1)单目标定或双目标定中,在内参固定的情况下,计算最佳外参。OpenCV中对应的函数为findExtrinsicCameraParams2。
(2)单目标定中,在内外参都不固定的情况下,计算最佳内外参。OpenCV中对应的函数为calibrateCamera2。
(3)双目标定中,在左右相机的内外参及左右相机的位姿都不固定的情况下,计算最佳的左右相机的内外参及最佳的左右相机的位姿矩阵。OpenCV中对应的函数为stereoCalibrate。
本文文阅读前提是你已经对LM(Levenberg-Marquardt)算法有足够的了解。因为本文主要是分析LM算法在相机标定中应用。
本文的分析是基于OpenCV的源码,所以可参见OpenCV的源码阅读此文。
0变量设置
设标定板上角点数为m,标定过程中拍摄n幅视图(对双目标定而言,左右相机各抓取n幅视图)。
关于相机的成像模型和畸变模型,我这里就不占空间了,详见OpenCV官方文档或相关论文。我用如下函数表示:
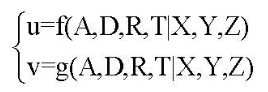
其中,(u,v)是像素坐标,(X,Y,Z)是世界坐标,R=(r1, R2, R3)T是旋转外参,T=(T1, T2, T3)T是平移外参,A=(fx, fy, cx, cy)T是投影内参,D=(k1, k2, p1,p2, k3, k4, k5, k6, s1, s2, s3, s4, a, b)T是畸变内参。
纵所周知,(u,v)是存在畸变的(后文称之为畸变坐标),我们用(uu,vv)表示(u,v)对应的非畸变的坐标(后文称之为标准坐标)。我们用findChessboardCorners提取的角点坐标就被当作是标准坐标。
1计算最佳外参
在内参固定的情况下,我们需要计算最佳外参。于是成像模型简化为:
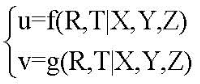
对于m个角点则有如下方程:
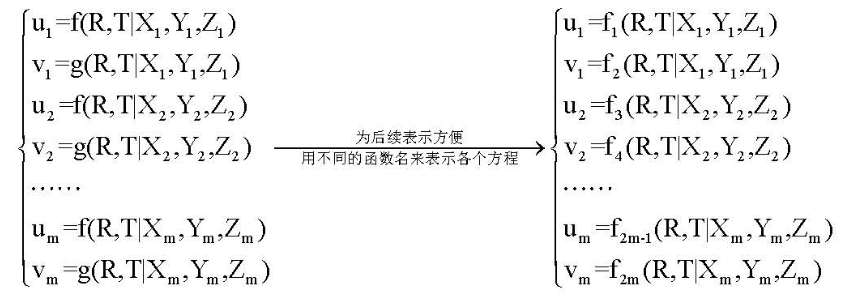
其中(Xi, Yi, Zi)是已知项。计算雅可比矩阵如下:
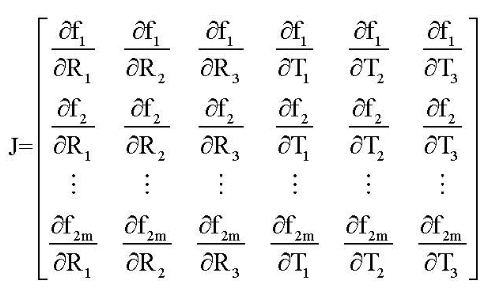
由J可得J和JTJ。
若给定初值(R0, T0)则可得畸变角点序列uv=(u1,v1, u2,v2,…,um,vm)T。若findChessboardCorners获得的标准角点序列为uuvv=(uu1, vv1, uu2, vv2, …, um, vm)T,则误差序列为E=uv-uuvv。于是最终的方程为:
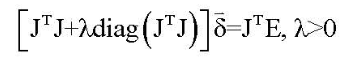
解方程后可得更精确的(R1, T1)=(R0, T0)-σ。
注意:以上可能与其它LM算法介绍有些差异。按大多数LM算法的介绍文档应是E=uuvv-uv, (R1, T1) = (R0, T0) +σ。不过仔细观察会发现最终结果其实一样的。我只不过是为了与OpenCV中源码对应才这样写的。
2计算最佳内外参
在内外参都不固定的情况下,成像模型应为:
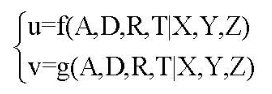
与计算最佳外参不同。计算最佳外参是针对一幅视图,优化目标是使此幅视图的重投影误差最小。而计算最佳内外参,是针对多幅视图,优化目标是使所有视图的重投影误差之和最小。每幅视图有各自的外参,但共用相同的内参。所以每幅视图像上的角点仅对内参和各自的外参存在偏导,对其它视图的外参的偏导为0。于是雅可比矩阵为:
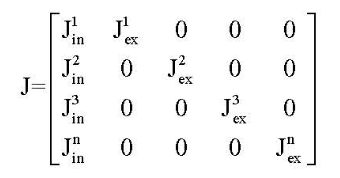
其中,Jini和Jexi是第i幅视图对内参和自身外观的雅可比矩阵。Jini是n×18矩阵(因为18个内参所以18列),Jexi是n×6矩阵(因为6个外参所以6列),所以J是(n*n)×(18+6*n)的矩阵。
可算得:
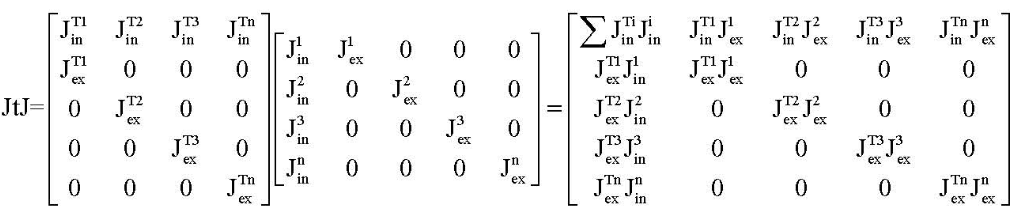
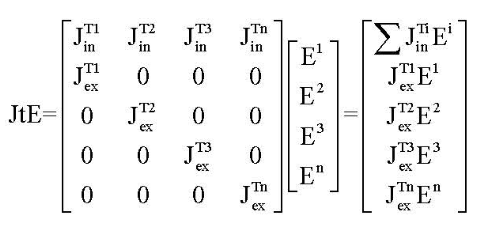
3计算最佳左右相机的内外参及最佳左右相机的位姿矩阵
此步骤中的优化参数是两相机间的位姿矩阵(R, T),两相机的内参(A1, D1, A2, D2)及左两机外参序列(R1i, T1i)。其中左相机的外参(R2i, T2i)=(RR1i, RT1i+T)。于是左相机每幅视图上的角点只对(A1, D1, Ri, Ti)有偏导,对其它参数的偏导为0。而右相机每幅视图上的角点只对(R, T, A2, D2, R1i, T1i)有偏导,对其它参数的偏导为0。其中,对(R, T, R1i, T1i)的偏导来源于对(R2i, T2i)的偏导。





 本文详细介绍了LM(Levenberg-Marquardt)算法在相机标定中的三种应用场景,包括计算最佳外参、内外参以及双目相机系统的内外参与位姿矩阵。通过解析OpenCV源码,深入探讨了LM算法的具体实现过程。
本文详细介绍了LM(Levenberg-Marquardt)算法在相机标定中的三种应用场景,包括计算最佳外参、内外参以及双目相机系统的内外参与位姿矩阵。通过解析OpenCV源码,深入探讨了LM算法的具体实现过程。
















 1241
1241

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








