整数和浮点数在内存的存储

目录

1.大小端

2.整型在内存的存储

3.浮点型在内存的存储

---

 

1.大小端

int main()
{
	int a = 0x11223344;
	return 0;
}

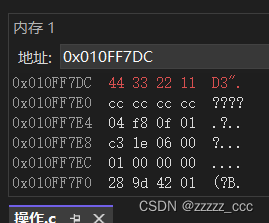
我们看出一个问题，为什么a按字节为单位，它的数据是倒着存储的呢？ 

1.1什么是大小端？

字节在超过数据存储的时候就会有存储顺序的问题，在不同的存储顺序，我们分为大端存储和小端存储。

大端存储：低位字节数据存储在高地址处，高位字节数据存储在低地址处。

小端存储：低位字节数据存储在低地址处，高位字节数据存储在高地址处。

1.2为什么要分大小端

因为寄存器宽度⼤ 于⼀个字节，就会存在着⼀个如何将多个字节安排的问题。因此就导致了⼤端存储模式和⼩端存储模式。

2.整型在内存的存储

整型在内存的存放模式就是二进制的补码来进行存储的 

在计算机系统中，数值⽤补码来表⽰和存储。 原因在于，使⽤补码，可以将符号位和数值域统处理； 同时，加法和减法也可以统⼀处理（CPU只有加法器）此外，补码与原码相互转换，其运算过程是 相同的，不需要额外的硬件电路。

3.浮点型在内存的存储

int main()
{
	int n = 7;
	float* pf = (float*)&n;
	printf("n的值为：%d\n", n);
	printf("*pf的值为：%f\n", *pf);
	*pf = 7.0;
	printf("n的值为：%d\n", n);
	printf("*pf的值为：%f\n", *pf);
	return 0;
}

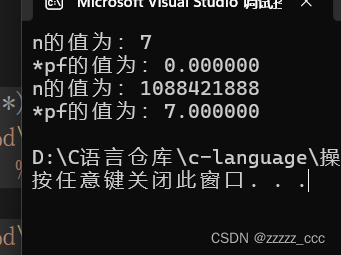
我们可以看出为什么输出没有正确的打出对应的数值

浮点数在计算机内部的表⽰⽅法是根据国际标准IEEE（电⽓和电⼦⼯程协会） 754，任意⼀个⼆进制浮点数V可以表⽰成下⾯的形式：

V   =  (−1) 的s次方∗ M ∗ 2的E次方

• (−1) S 表⽰符号位，当S=0，V为正数；当S=1，V为负数

• M 表⽰有效数字，M是⼤于等于1，⼩于2的

• E 表⽰指数位

举例来说：

⼗进制的5.0，写成⼆进制是 101.0 ，相当于 1.01×2^2 。

那么，按照上⾯V的格式，可以得出S=0，M=1.01，E=2。

⼗进制的-5.0，写成⼆进制是 -101.0 ，相当于 -1.01×2^2 。那么，S=1，M=1.01，E=2。

规定：

对于32位的浮点数，最⾼的1位存储符号位S，接着的8位存储指数E，剩下的23位存储有效数字M

对于64位的浮点数，最⾼的1位存储符号位S，接着的11位存储指数E，剩下的52位存储有效数字M

---

这就是所有内容啦，如有错误批评指正，谢谢。