【LeetCode题解】77. 组合

最新推荐文章于 2025-09-05 20:46:39 发布

原创最新推荐文章于 2025-09-05 20:46:39 发布 · 167 阅读

0 ·

CC 4.0 BY-SA版权

LeetCode题解专栏收录该内容

95 篇文章

订阅专栏

本文探讨了组合问题的两种高效求解方法，一种是通过回溯算法寻找所有可能的k个数的组合，另一种是利用位串和字典序进行巧妙的组合求解，避免了重复和遗漏。

给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。

示例:

输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

题解：

这题是组合问题，我用的常规回溯：

找到list中最后一个元素 i，往list中按序添加 i 到 n+1之间的元素，直到 list长度=k
若list长度<k，并且最后一个元素已经是 n了，再添加就会越界了，在递归开始判断并剪去这部分

class Solution {
    List<List<Integer>> ret = new ArrayList<>();
    public List<List<Integer>> combine(int n, int k) {
        //组合，而非排列
        List<Integer> list = new ArrayList<>();
        par(n,k,list);
        return ret;
    }
    
    void par(int n, int k ,List<Integer> list){
        //这里剪枝会提高不少效率,避免多余的递归
        if(list.size()!=0 && list.size()<k && list.get(list.size()-1)==n){
            return ;
        }
        if(list.size() == k){
            ret.add(new ArrayList(list));
            return;
        }
        int i=1;
        if(list.size()!=0){
            i = list.get(list.size()-1)+1;
        }
        for(; i<=n ; i++){
            list.add(i);
            par(n,k,list);
            list.remove(list.size()-1);
        }
    }
}

这题跑完排行只到一半左右，看了下官方题解，果然有种很巧妙的解法：

图片来自官方题解

官方解用的是字典序，很巧妙，因为这题考的是组合，可以转换成排列求解
在计算机中如果使用位串表示集合的子集会便于集合的运算（补集、交、并）以及排列组合（如n个元素的子集 = [ 00..000=空集，00..001,00..010,00..011,00..100 。。。。。11..111 共 2^n个）
对于n = 4 ，k = 2 的情况如果将 [ 4,3,2,1 ] 抽象成位串，则符合条件的解为 [ 0,0,1,1 ] 、 [ 0,1,0,1 ] 、 [ 0,1,1,0 ] 、 [ 1,0,0,1 ] .........，排序方式按二进制位串的大小从小到大依次排列（即十进制的3,5,6,9.....），这样做的好处是显然可以看出不会遗漏解
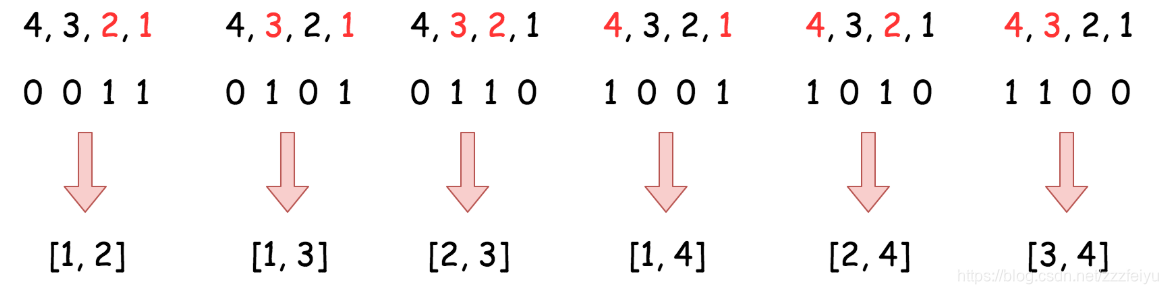
抽象出来位串并不是真的二进制，该解是取一个长度= k+1 的公共容器list，每次取前k项，同时在list内按字典序进行变动

class Solution {
  public List<List<Integer>> combine(int n, int k) {
    // init first combination
    LinkedList<Integer> nums = new LinkedList<Integer>();
    for(int i = 1; i < k + 1; ++i)
      nums.add(i);
    nums.add(n + 1);

    List<List<Integer>> output = new ArrayList<List<Integer>>();
    int j = 0;
    while (j < k) {
      // add current combination
      output.add(new LinkedList(nums.subList(0, k)));
      // increase first nums[j] by one
      // if nums[j] + 1 != nums[j + 1]
      j = 0;
      while ((j < k) && (nums.get(j + 1) == nums.get(j) + 1))
        nums.set(j, j++ + 1);
      nums.set(j, nums.get(j) + 1);
    }
    return output;
  }
}