启发式合并笔记

核心思想：两个集合合并 将元素数量少的加入到元素数量多的里面

时间复杂度：<=O(nlgn)

HNOI2009, 梦幻布丁 - 题目 - Daimayuan Online Judge

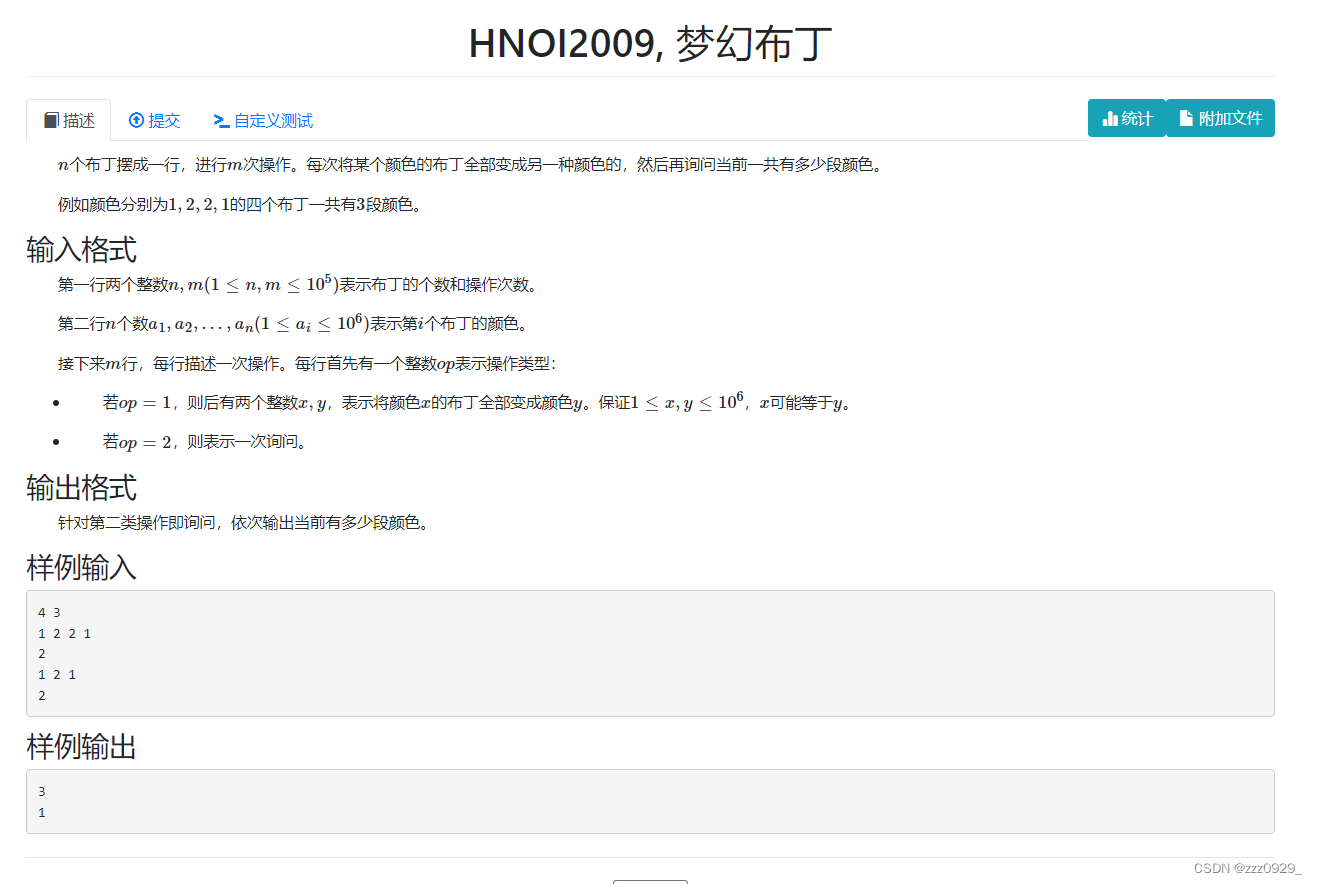
求颜色段数 小技巧：

算到第n+1个 输出答案是ans-1

更换颜色维护信息 :

ans -= ((a[k] != a[k - 1]) + (a[k] != a[k + 1]));

 a[k] = col;

 ans+= ((a[k] != a[k - 1]) + (a[k] != a[k + 1]));

（每一次边界都被加减抵消）

可减少边界判断

用vector<int>pos 来记录每个集合的元素  合并时候比较两个集合大小 

#define _CRT_SECURE_NO_WARNINGS 1
#include<bits/stdc++.h>
using namespace std;

typedef unsigned long long ull;
#define V vector
#define pii pair<int,int> 
#define ll long long
const int inf = 0x3f3f3f3f;
const int mod = 1e9 + 7;
const int N = 1e6 + 10;
const int M = 500;

//pos记录颜色为i的!!下标!!集合 颜色为a[pos[i]]
V<int>pos[N];
int n, m;
int a[N];
int main()
{
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i++)
	{
		scanf("%d", a + i);
		pos[a[i]].push_back(i);
	}
	int ans = 0;
	// 算到n+1 后面简化尾部特判
	for (int i = 1; i <= n + 1; i++)
		if (a[i] != a[i - 1])
			ans++;
	while (m--)
	{
		int op; scanf("%d", &op);
		if (op == 2)printf("%d\n", ans - 1);
		else
		{
			int x, y; scanf("%d%d", &x, &y);
			if (x == y)continue;
			//让 pos[y]为大集合 x到y里
			if (pos[x].size() > pos[y].size())
				pos[x].swap(pos[y]);
			if (pos[y].empty())continue;
			//模拟  此时无需判断尾部 a[n+1]=0颜色始终不一样
			auto modify = [&](int k, int col)
			{
				ans -= ((a[k] != a[k - 1]) + (a[k] != a[k + 1]));
				a[k] = col;
				ans+= ((a[k] != a[k - 1]) + (a[k] != a[k + 1]));
				//printf("%d\n", ans-1);
			};
                      // 注意颜色a[    ]
			int col = a[pos[y][0]];
			for (int k : pos[x])
			{
				modify(k, col);
                //x中的元素加入y中
				pos[y].push_back(k);
			}
			pos[x].clear();
		}
	}
}

DSU On Tree  （启发式思想，易懂简单）

dsu on tree 思想：
建树 从底往上 将所有轻儿子信息合合并到当前节点的重儿子中

时间复杂度 <=O(nlgn） 空间复杂度O(n)

模板：

int tot, n;
//id 记录编号tot对应的节点   hs[i] i的重儿子  
int id[N], sz[N], l[N], r[N], hs[N];
V<int>h[N];


void dfs_pre(int u, int fa)
{
	l[u] = ++tot;
	id[tot] = u;
	sz[u] = 1;
	hs[u] = -1;
	for (int v : h[u])
		if (v != fa)
		{
			dfs_pre(v, u);
			sz[u] += sz[v];
			//记录重儿子
			if (hs[u] == -1 || sz[v] > sz[hs[u]])
				hs[u] = v;
		}
	r[u] = tot;
}
void dfs_solve(int u, int fa, bool ok)
{
	//访问 轻儿子
	for (int v : h[u])
		if (v != fa && v != hs[u])
			dfs_solve(v, u, false);
	if (hs[u] != -1)
		//不为叶子节点 ，有重儿子
		dfs_solve(hs[u], u, true);
	auto add = [&](int x)
	{
		
	};
	auto del = [&](int x)
	{
		
	};
	for (int v : h[u])
		if (v != fa && v != hs[u])
		{
			//轻儿子加入重儿子
			for (int i = l[v]; i <= r[v]; i++)
				add(id[i]);
		}
	//加入u本身,以u为子树的块 遍历结束 
	add(u);
	//每次访问完轻儿子后，删除遗留信息
	if (!ok)
	{
		for (int i = l[u]; i <= r[u]; i++)
			del(id[i]);
	}
}

IOI2011, Race - 题目 - Daimayuan Online Judge

前置知识：

令  dep1[ i ]表示 i 到根节点的边数量（深度） ,dep2[ i ]表示 i 到根节点的路径权值总和

那么 若节点 u 的两个儿子 i  j 互通

1）要走的边数 = dep1[ i ]+dep[ j ]-2*dep[ u ]  

2）所加的权值 k=  dep2[ i ]+dep2[ j ]-2*dep[ u ]

那么运用DSU 算法 在合并区间的时候 我只需要 用一个map 函数 记录 当前的根 u 的重儿子里面 有没有一个节点 i 的权值 等于 k+ 2*dep[ u ]-dep2[ j ]（上述（2）转化） 若有，则 i - j 满足题意（但不一定边数最小）

于是贪心的遍历所有可能答案

#define _CRT_SECURE_NO_WARNINGS 1
#include<bits/stdc++.h>
using namespace std;

typedef unsigned long long ull;
#define V vector
#define pii pair<int,int> 
#define ll long long
const int inf = 0x3f3f3f3f;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
const int M = 500;
                  //dep1 深度  dep2 i 到根的权值
int n, k,sz[N],dep1[N],dep2[N],tot,l[N],r[N];
int id[N],hs[N];
V<pii>h[N];
// mp  边权为 ll 时后的最小边数
map<ll, int>mp;
int ans;
void dfs1(int u, int fa)
{
	l[u] = ++tot;
	sz[u] = 1; hs[u] = -1;
	id[tot] = u;
	for (pii i : h[u])
	{
		int v = i.first, w = i.second;
		if (v == fa)continue;
		dep1[v] = dep1[u]+1;
		dep2[v] = dep2[u] + w;
		dfs1(v, u);
		sz[u] += sz[v];
		if (hs[u] == -1 || sz[hs[u]] < sz[v])hs[u] = v;
	}
	//printf("u:%d  1:%d  2:%d\n", u, dep1[u], dep2[u]);
	r[u] = tot;
}
void dfs2(int u, int fa, bool ok)
{
	for (auto i: h[u])
		if (i.first != fa && hs[u] != i.first)
			dfs2(i.first, u, false);
	if (hs[u] != -1)
		dfs2(hs[u], u, true);
	//求val最小
	auto add = [&](int x)
	{
		if (mp[dep2[x]])
			mp[dep2[x]]=min(mp[dep2[x]],dep1[x]);
		else mp[dep2[x]] = dep1[x];
	};
	// 更新当前树里的答案
	auto query = [&](int x)
	{
		//求出与x节点能成k的另一个节点需要的权值d
		ll d = 2LL * dep2[u] - dep2[x] + k;
		if (mp[d])
			ans = min(ans, mp[d] + dep1[x] - 2 * dep1[u]);
		//printf("%d\n", ans);
	};
	for (pii i : h[u])
	{
		int v = i.first, w = i.second;
		if (i.first != fa && hs[u] != i.first)
		{
			for (int j = l[v]; j <= r[v]; j++)
				query(id[j]);
			for (int j = l[v]; j <= r[v]; j++)
				add(id[j]);
		}
	}
	query(u); add(u);
	if (!ok)
	{
		mp.clear();
	}
}

int main()
{
	scanf("%d%d", &n, &k);
	ans = n + 1;
	for (int i = 1; i < n; i++)
	{
		int u, v, w;
		scanf("%d%d%d", &u, &v, &w);
		h[u].push_back({ v,w });
		h[v].push_back({ u,w });
	}
	dfs1(0, -1);
	dfs2(0, -1, false);
	if (ans >= n + 1)printf("-1");
	else printf("%d", ans);
	puts("");
	return 0;
}