关于Batch Normalization

最新推荐文章于 2025-07-10 21:37:38 发布

一只tobey

最新推荐文章于 2025-07-10 21:37:38 发布

阅读量1.1k

点赞数

CC 4.0 BY-SA版权

分类专栏：方法

本文链接：https://blog.youkuaiyun.com/zz2230633069/article/details/94588738

论文同时被 2 个专栏收录

40 篇文章

订阅专栏

方法

15 篇文章

订阅专栏

本文深入解析BatchNormalization在深度学习中的作用机制，包括其计算公式、参数解析及在不同维度上的应用，如BatchNorm1d、BatchNorm2d和BatchNorm3d。探讨了BN如何通过减少内部协变量偏移来加速深层网络的训练，并分析了其在训练和评估阶段的统计计算方式。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

参考相关文档：关于BN的讲解论文来自于下面的第二个

[深度学习中 Batch Normalization为什么效果好？]

[《Batch Normalization Accelerating Deep Network Training by Reducing Internal Covariate Shift》阅读笔记与实现]

[从Bayesian角度浅析Batch Normalization]

[Deep Learning论文笔记]

[cs231n学习笔记-激活函数-BN-参数优化]

[Batchnorm原理详解]

[ 深度学习中的Normalization模型]

计算公式：

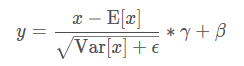
上面的均值和方差都是在每一个维度计算的，gama,beta都是可以学习的向量，size为C（channels）就是特征层的大小。

在默认情况下，在训练这个layer的期间保持运行估计（keep running estimates of its computed mean and variance）计算出来的均值和方差，而这些均值和方差在evaluation期间被用来normalization.

如果参数`track_running_stats` is set to ``False``，那么this layer then does not keep running estimates, and batch statistics are instead used during evaluation time as well.

参数momentum不是优化器里面的和传统的动量概念，该参数用于计算running_mean和running_var，当设置为None的时候是累积移动平均（即简单平均值）。数学上表示如下，其中最左边的参数是估计的统计量，最右边的参数是新观察值。

Because the Batch Normalization is done over the `C` dimension, computing statistics on `(N, H, W)` slices, it's common terminology to call this Spatial Batch Normalization.

参数eps是添加到分母的值，为了增加数值的稳定性。

参数affine是一个bool值，当为True的时候，该模块具有可学习的仿射参数weight和bias（就是上述公式里面的gama和beta），如果是False那么weight==1,bias==0,不是可学习的参数。其中weight和bias，shape都是一个向量并且维度等于特征层的数目。

@weak_module
class _BatchNorm(Module):
    _version = 2
    __constants__ = ['track_running_stats', 'momentum', 'eps', 'weight', 'bias',
                     'running_mean', 'running_var', 'num_batches_tracked']

    def __init__(self, num_features, eps=1e-5, momentum=0.1, affine=True,
                 track_running_stats=True):
                super(_BatchNorm, self).__init__()
        self.num_features = num_features
        self.eps = eps
        self.momentum = momentum
        self.affine = affine
        self.track_running_stats = track_running_stats
        if self.affine:
            self.weight = Parameter(torch.Tensor(num_features))
            self.bias = Parameter(torch.Tensor(num_features))
        else:
            self.register_parameter('weight', None)
            self.register_parameter('bias', None)
        if self.track_running_stats:
            self.register_buffer('running_mean', torch.zeros(num_features))
            self.register_buffer('running_var', torch.ones(num_features))
            self.register_buffer('num_batches_tracked', torch.tensor(0, dtype=torch.long))
        else:
            self.register_parameter('running_mean', None)
            self.register_parameter('running_var', None)
            self.register_parameter('num_batches_tracked', None)
        self.reset_parameters()
    # 后面还有内容，定义其他方法


@weak_module
class BatchNorm1d(_BatchNorm):
    @weak_script_method
    def _check_input_dim(self, input):
        if input.dim() != 2 and input.dim() != 3:
            raise ValueError('expected 2D or 3D input (got {}D input)'
                             .format(input.dim()))
    # 仅仅只有上面一个函数，下面的情况相同，都是该class的完整代码，调用了上面的父类

@weak_module
class BatchNorm2d(_BatchNorm):
    @weak_script_method
    def _check_input_dim(self, input):
        if input.dim() != 4:
            raise ValueError('expected 4D input (got {}D input)'
                             .format(input.dim()))

@weak_module
class BatchNorm3d(_BatchNorm):
        @weak_script_method
    def _check_input_dim(self, input):
        if input.dim() != 5:
            raise ValueError('expected 5D input (got {}D input)'
                             .format(input.dim()))
    def __init__(self, num_features, eps=1e-5, momentum=0.1, affine=True,
                 track_running_stats=True):

# BN的实现具体
import torch
import torch.nn as nn

m = nn.BatchNorm2d(2, affine=True)  # True是默认值，weight(gamma)和bias(beta)将被使用，如果设置为False，则weight和bias都为None，公式中计算的表现为gamma为1，beta为0
input = torch.randn(2, 2, 3, 4)
output = m(input)

print("输入图片：")
print(input)
print("归一化权重(公式中的gamma)：")
print(m.weight)
print("归一化偏置(公式中的beta)：")
print(m.bias)

print("归一化的输出：")
print(output)
print("输出的尺度：")
print(output.size())

print("输入的特征层的第一个维度：")
print(input[:, 0, :, :])
firstDimenMean = torch.mean(input[:, 0, :, :])  # 该层的均值
firstDimenVar = torch.var(input[:, 0, :, :], False)  # 该层的方差
"""注意Bessel's Correction贝塞尔校正在BN里面是不会被使用，本人经过测试，如果设置为True那么得到的结果和BN的结果不一致"""
print('eps 值', m.eps)  # 这个就是公式里面的防止分母为0的eps
print(f"输入的第一个维度平均值：{firstDimenMean}")
print(f"输入的第一个维度方差：{firstDimenVar}")
myout = torch.zeros_like(output)  # 用公式算的的输出初始化
myout[:, 0, :, :] = \
    ((input[:, 0, :, :] - firstDimenMean)/(torch.pow(firstDimenVar+m.eps, 0.5)))\
    * m.weight[0] + m.bias[0]
print(f'output输出： {output[:, 0, :, :]}', f'\n myoutput输出：{myout[:, 0, :, :]}')
print('判断这两个是不是相等的(对应数值相等为1，否则为0)：', myout[:, 0, :, :] == output[:, 0, :, :])
"""
可以观察数值是相等的，但是具体的数值，即小数后面的很多位之后就不相等，
所以计算的结果还是有一点小误差
"""