Gradient Descent
在学习Regression的时候,我们第一次接触到gradient descent这个概念,我们知道了它是用于找到最优的function,计算loss function的一种方法。我们的目的是计算L(θ\thetaθ)最小的时候,即找到最优的参数θ∗\theta^{*}θ∗.
最小二乘法与梯度下降法的关系:
相同点:
1.本质相同:两种方法都是在给定已知数据的前提下对dependent variables算出一个一般性的估值函数。然后对给定新数据的dependent variables进行估算。
2.目标相同:都是在已知数据的框架内,使得估算值与实际值的总平方差尽量更小(事实上未必一定要使用平方。
不同点:
1.实现方法和结果不同:最小二乘法是直接对loss function求导找出全局最小,是非迭代法。
2.而梯度下降法是一种迭代法,先给定一个www,然后向loss function下降最快的方向调整www,在若干次迭代之后找到局部最小。梯度下降法的缺点是到最小点的时候收敛速度变慢,并且对初始点的选择极为敏感

上面我们把公式写成向量的形式,θ0\theta^{0}θ0代表参数的向量形式,∇L(θ)\nabla L ( \theta )∇L(θ)就是对loss function的偏微分,也叫gradient。下面我们可视化求解的过程:
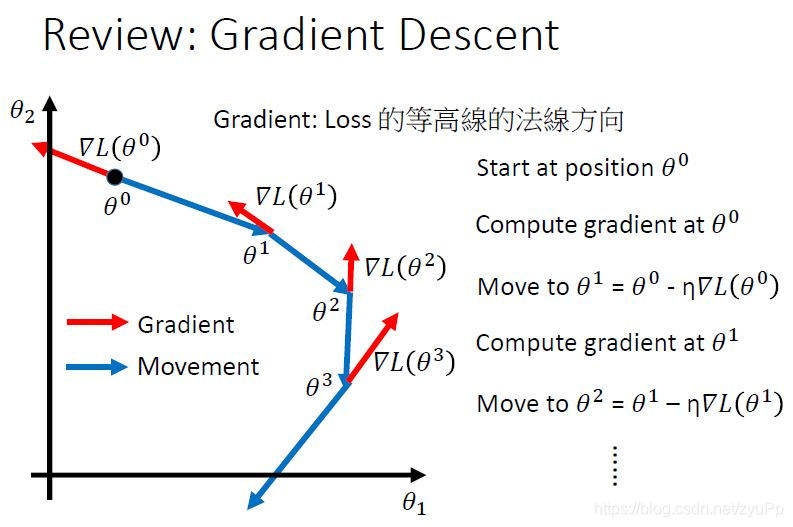
首先随机取一个起始点θ0\theta^{0}θ0,计算这个点在loss function的gradient,gradient就是红色的箭头(一个向量),然后用gradient乘以learning rate η\etaη再取负号,就是蓝色的箭头,最后加上θ0\theta^{0}θ0,就是θ1\theta^{1}θ1。
现在我们要让梯度下降法表现得更好,有什么方法呢?
Tip 1:Tuning调整 your learning rate
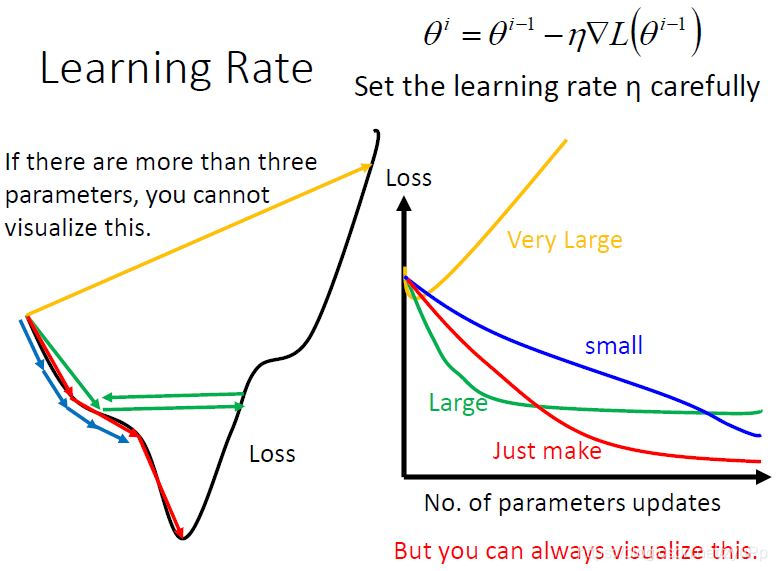
如果learning rate设置得刚好,会正确取到最低点(红色线)
如果learning rate设置得太小,会很慢(蓝色线);
如果learning rate设置得有点大,因为步伐太大了,无法去到最低点(绿色线);
如果learning rate设置得很大,就会飞出去(黄色线);
当参数超过3个以后,我们没法可视化它的表现,但是我们可以看看“参数的变化parameters updates” 对 ”Loss的变化“ 。 我们可以看参数变化时,loss值变化的趋势,来判断该怎么调整learning rate
Adapative Learning Rates
我们希望可以有自动调整的learning rate,第一个idea是根据运行到达的次数来自动调整,我们知道一开始离最低点还有点远,所以可以用比较大的learning rate,当迭代一定次数后,你逐渐靠近目标,这时候就应该减少learning rate。例子中,我们用t代表次数。
例如ηt=η/t+1\eta ^ { t } = \eta /\sqrt { t + 1 }ηt=η/t+1, 当步数t越大,那么ηt\eta ^ { t }ηt的值就变小

但是这样是不够的,对于不同的参数,都最好给不同的learning rate,其中有一个实现的方式叫做 Adagrad
Adagrad

Adagrad 是每一个参数的learning rate都除以之前算出来所有的微分值的RMS(root mean square)均方根。下面是计算步骤演示:

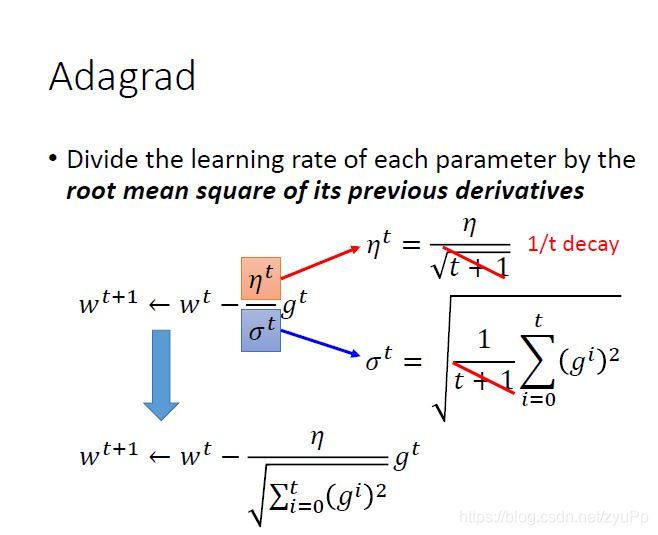
把公式σt\sigma^{t}σt带进去,可以删去t+1\sqrt { t + 1 }t+1,gig^igi是之前的微分值,最后的公式是:
wt−η∑i=0t(gi)2gtw ^ { t } - \frac { \eta } { \sqrt { \sum _ { i = 0 } ^ { t } ( g ^ { i } ) ^ { 2 } } } g ^ { t }wt−∑i=0t(gi)2ηgt
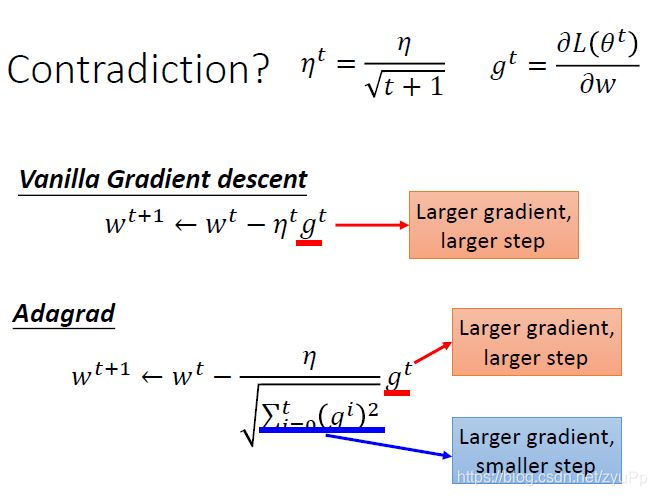
其实adagrad这个方法,到后面的运行时间会越来越慢,因为添加了time decay
除了有Adagrad,目前为止,Adam方法是比较好用和稳定的方法。
除了learning rate,影响参数更新的还有gradient,gradient越大,更新得越快。 但是在Adagrad,就出现个奇怪的现象,看上图;gtg^tgt变大,参数更新得越快,但是gig^igi越大,又会参数更新步伐就越小,这样就有互相冲突的现象,所以应该怎么解释这个问题呢?

第一种最直观的解释,就是为了看出来反差,你可以看到某个graident突然地变得很大或者很小,形成一种反差。
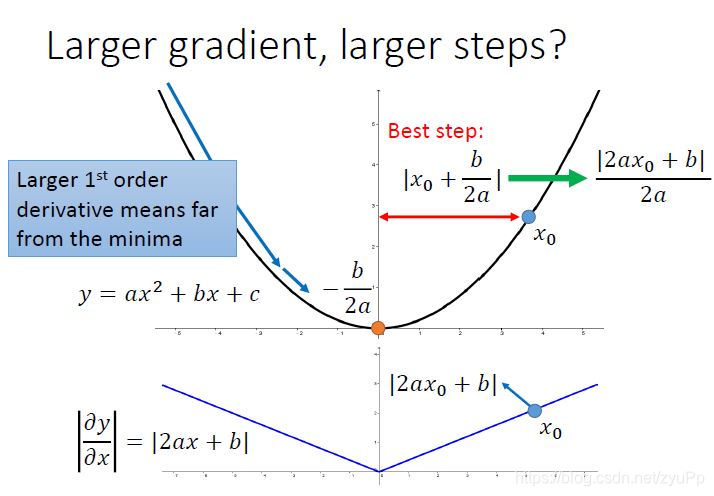
第二种解释:假设有个二次函数y=ax2+bx+cy=ax^2+bx+cy=ax2+bx+c,对xxx求微分就是2ax+b2ax+b2ax+b,我们知道二次函数的最低点是−b2a- \frac { b } { 2 a }−2ab。
我们现在随机选择一个点x0x_{0}x0,那最好的一步到位的距离就是x0+b2ax_{0}+\frac { b } { 2 a }x0+2ab,化解为2ax0+b2a\frac { 2 a x _ { 0 } + b } { 2 a }2a2ax0+b,所以x0x_{0}x0的微分就是下面那个图的位置,如果算出来的微分越大,离原点越远,最好的步伐和微分值的大小成正比,但是这个事情只是在只考虑一个参数的时候,才成立。
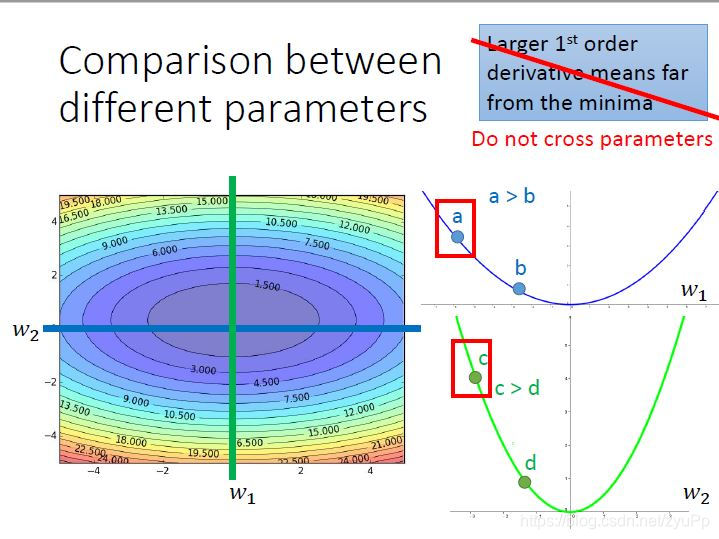
上图是同时考虑w1和w2两个参数,可以看出两边的等高线的变化是不同,的,在各自的范围里考虑,a>b,c>d,但是考虑a和c的时候,其实c是离最低点比较近,a比较远。 步伐和微分值的大小成正比这个论述,只有在不考虑跨参数的时候才成立。
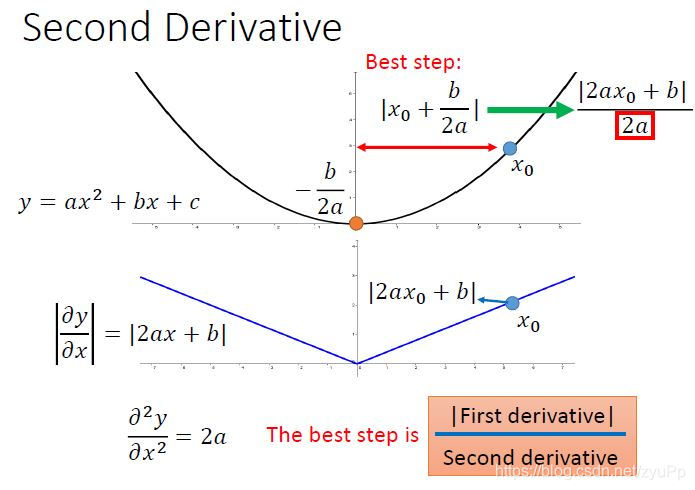
我们知道2a2a2a是y对x的二次微分,所以可知最好的步伐是
(一次微分)/(二次微分)
在考虑跨参数的时候,我们就要把二次微分考虑进来
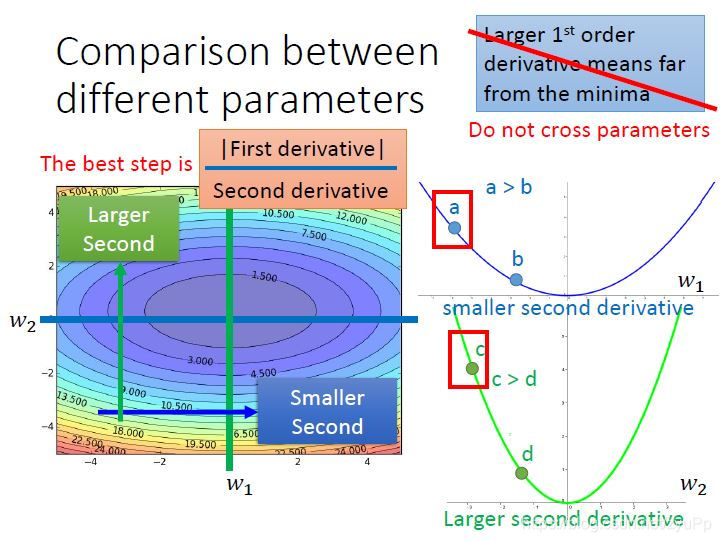
所以比较a和c的时候,我们要用a点的微分值除以w1的二次微分,c点的微分值除以w2的二次微分,这样比较才会看到这两个点离最低点的距离,因为w1是比较平滑的,所以二次微分比较小,w2的二次微分就比较大。
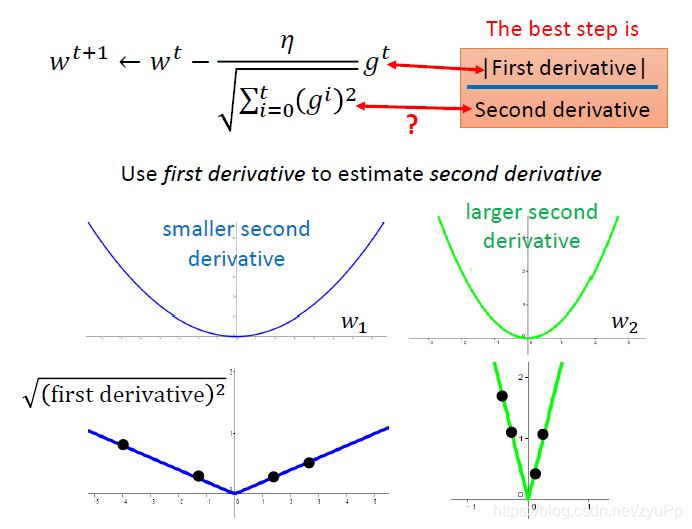
把公式对照着刚刚说的东西看一下,你会发现gtg^tgt就是一次微分,而下面的previous derivatives的均方根就是二次微分,为什么呢?
从上图可以看到,我们对一次微分带入式子中,在图上sample足够多的点,我们就可以看到比较平滑的w1,一次微分的取值都是比较小,比较陡峭的w2的一次微分值都是比较大的,从而反映了二次微分的大小
Tip2 : Stochastic Gradient descent随机梯度下降

Batch Gradient Descent 批量梯度下降是常用的梯度下降方法,它就是我们上面一直使用的方法,在计算Loss 值的时候,需要把所有的training examples的预测值和真实值y^\hat yy^的差都加起来再求平均。
Stochastic Gradient Descent就是随机梯度下降,区别在于它的Loss值只计算一个example的预测值和真实值的差,参数θi\theta^iθi也只需要求一次。
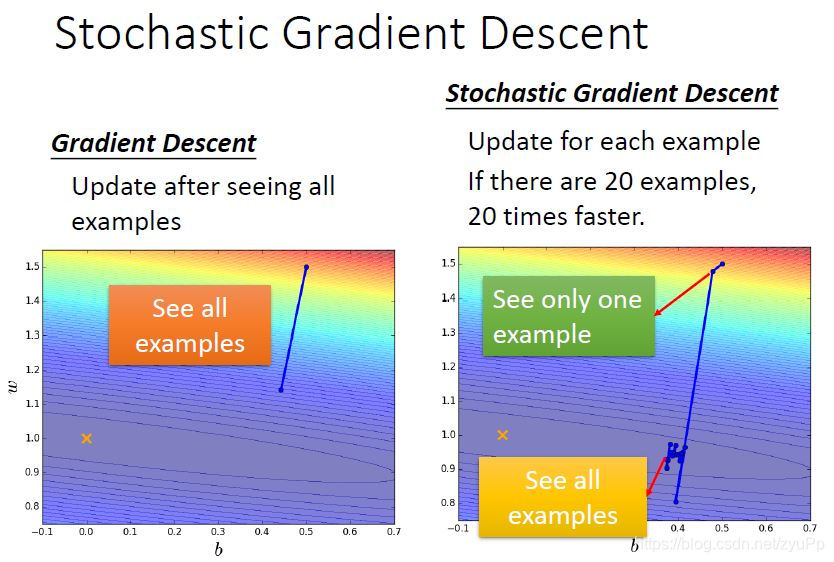
从上图可以看到,假设有20个examples,BGD是每次迭代都把20个example都观察一遍,才更新参数。而SGD是每看到一个example就会更新一次。也就是说BGD更新一次,SGD已经更新了20次。所以SGD的速度是比BGD快的,因为SGD走了20步,而BGD才走了一步。
Tip3 : Feature Scaling特征缩放
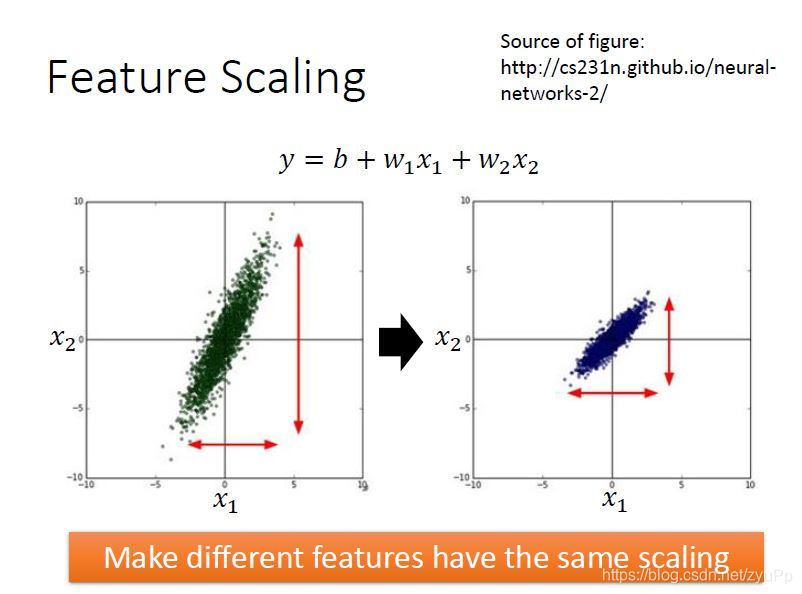
假设我们有一个model,x1x_1x1是宝可梦的进化前的cp值,x2x_2x2是生命值,代表着两个feature,如果x1和x2的分布不一样,左图可以看出x2的分布比x1大,所以我们要让它们的scale一样,为什么我们要这样做呢?
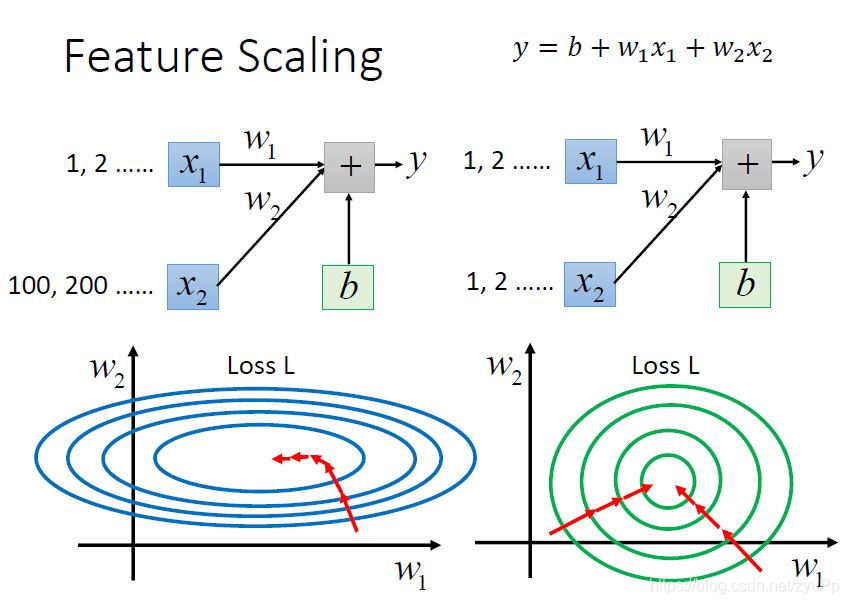
很明显可以看出来,当x1比x2的规模小一个级别,那么w1对y和loss的影响是很小的,而w2对y和loss影响就很大。根据左图,w1方向是比较平滑的,而w2方向是比较陡峭的。
当把x2进行scaling,就可以得到近似圆圈的图,这样子更新参数就会相对容易,看那条红色的路径就可以看出,没做scaling的时候,走的方向是弯曲的,不是直指中心,而scaling之后,就会直接往中心点靠近。
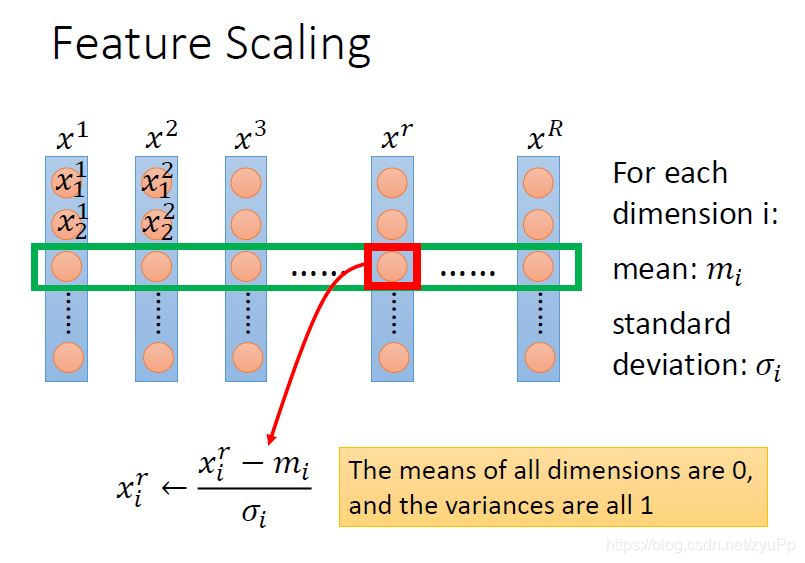
那么怎么做feature scaling呢?常用的做法是,对每个dimension i 都求一个mean均值,然后再算standard deviation标准差,最后对第r个example的第i个component更新xirx^r_ixir,新数值 =(原数值 - 均值)/ 标准差,也叫Z-score规范化。
做完这个规范化之后,所有dimension的mean是0,variance是1


我们来思考一个问题,是不是gradient descent每一次更新参数,Loss就一定会变小呢?其实不是的,loss不一定会下降的,我们知道当学习率learning rate很大的时候,Loss会飙升的。
数学问题:
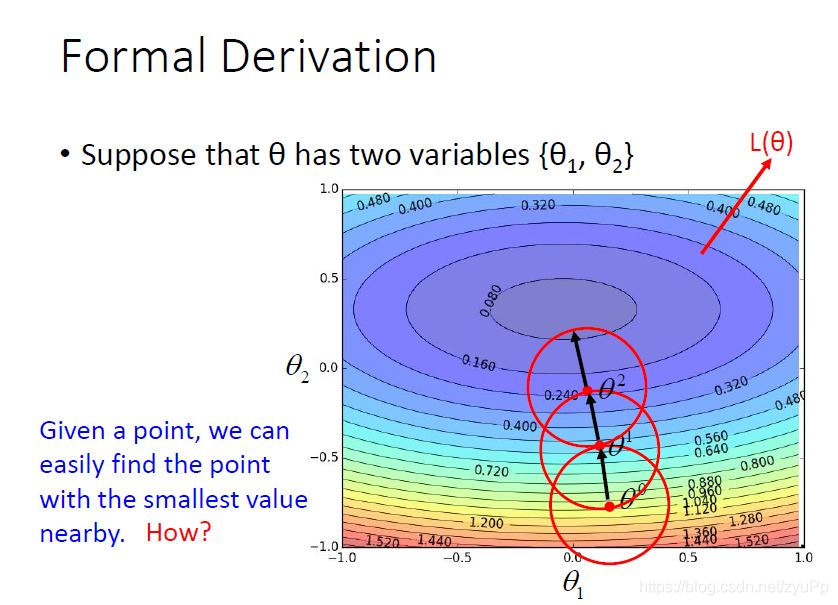
如果给你一个起始点θ0\theta^0θ0,我们可以在这个初始点附近找到最低的位置,红色圆圈就是那个附近的范围,然后更新中心点到θ1\theta^1θ1,不断的找以中心点为圆点找到最低点,我们的问题是 “如何在红色圈里面找到一个loss最小的参数呢?”
这里涉及到了一个数学原理,泰勒公式!
Taylor Series

上图是泰勒公式的表现形式,它是假设了h(x)是个可以无限微分的任意function,当xxx非常靠近x0x_{0}x0时,h(x)就约等于h(x0x_0x0)+h′h^{'}h′(x0x_0x0)(x−x0x-x_0x−x0) , 这个是只考虑了输入只有一个变量的时候
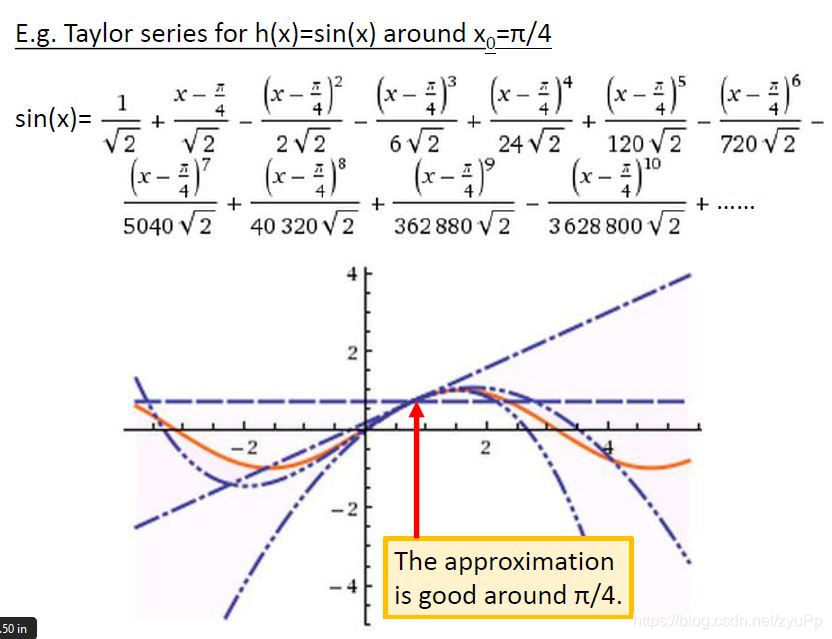
这里有个h(x)=sin(x) 的例子,最好的位置大概是接近π/4\pi/4π/4的时候,因为当x=π/4\pi/4π/4,那些带幂数的项都很小,可以忽略。

上图是多变量的泰勒公式,道理是一样的,当x和y接近x0x_0x0和y0y_0y0,还是可以忽略后面的项。
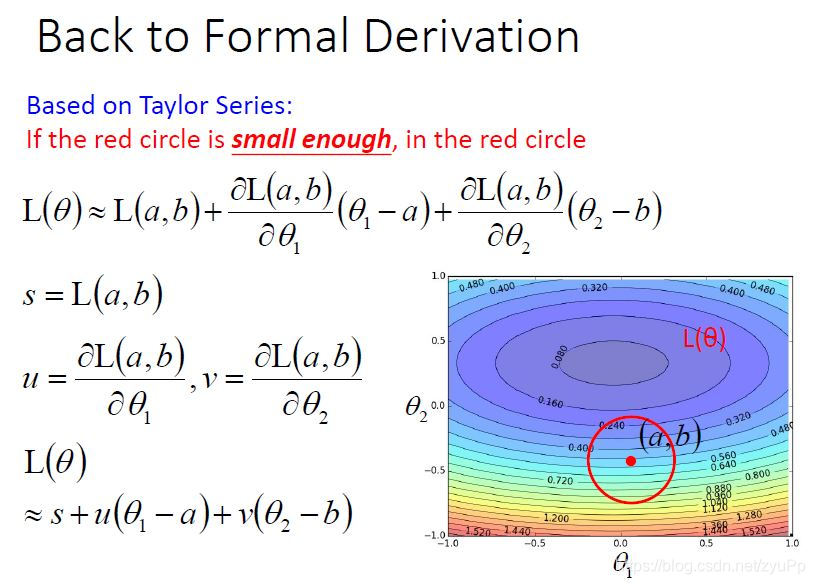
所以我们把泰勒公式应用到Loss function中,可以得到上图的公式,s、u、v都是常量,最后得到L(θ)=s+u(θ1−a)+v(θ2−b)L(\theta)=s+u(\theta_1-a)+v(\theta_2-b)L(θ)=s+u(θ1−a)+v(θ2−b)
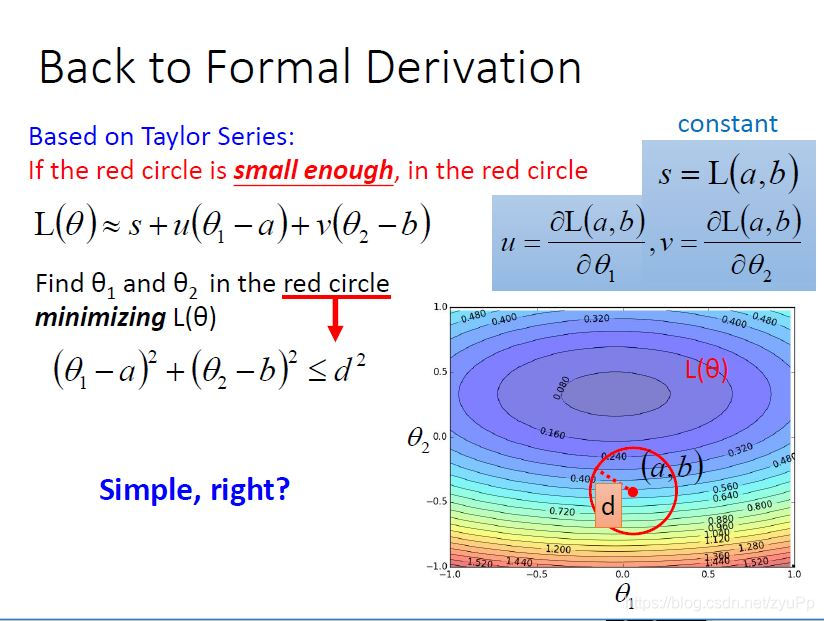

在红色圈圈内,找到θ1\theta_1θ1和θ2\theta_2θ2使得L(θ\thetaθ)最小,s和θ\thetaθ没有关系,所以可以无视,用Δθ\Delta \thetaΔθ来表示差值。其实可以把它们看成一个vector(Δθ1\Delta \theta_1Δθ1,Δθ2\Delta \theta_2Δθ2),有另外一个vector是(u,v)(u,v)(u,v),两个向量相乘,就是uΔθ1+vΔθ2u\Delta \theta_1+v\Delta \theta_2uΔθ1+vΔθ2。
为了让L(θ\thetaθ)最小,我们就令(Δθ1\Delta \theta_1Δθ1,Δθ2\Delta \theta_2Δθ2)的方向和(u,v)(u,v)(u,v)刚好相反,然后把(Δθ1\Delta \theta_1Δθ1,Δθ2\Delta \theta_2Δθ2)的长度拉长到圈圈的边缘,这个时候loss是最小的。η\etaη就是一个常量,使(Δθ1\Delta \theta_1Δθ1,Δθ2\Delta \theta_2Δθ2)的长度拉到边缘,然后再把公式分解开来,就回到了一条我们熟悉的公式,下图:

就是gradient descent的公式,而这个公式成立的前提是红色圈圈要够小,才会够精确,而红色圈的范围就代表了learning rate,所以为了让每次gradient descent,loss都变小,我们应该把learning rate设置得够小。
不过我们没有考虑二次幂进来,如果考虑进去,learning rate是可以大一点的,使用别的方法,牛顿法。
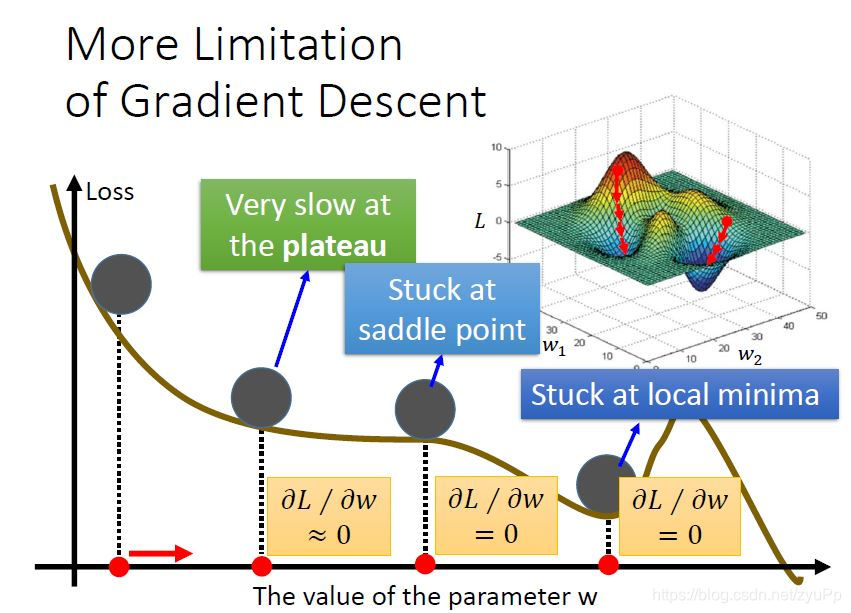
会卡在local minima,还有可能卡在鞍点saddle point,在泛函中,既不是极大值点也不是极小值点的临界点,叫做鞍点。真正最大问题是有可能微分值算得很小,但是处在高原的地方,因为太平坦








 本文深入探讨梯度下降法,解析其在寻找函数最优参数过程中的作用。对比最小二乘法,阐述梯度下降法的迭代特性及优缺点,讨论学习率调整、随机梯度下降、特征缩放等技巧,以及泰勒公式在确定最佳参数更新方向的应用。
本文深入探讨梯度下降法,解析其在寻找函数最优参数过程中的作用。对比最小二乘法,阐述梯度下降法的迭代特性及优缺点,讨论学习率调整、随机梯度下降、特征缩放等技巧,以及泰勒公式在确定最佳参数更新方向的应用。
















 395
395

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








