Leetcode 239 滑动窗口最大值 与堆排序kotlin语言(超时)接后续hash表完成
首先看题目描述:
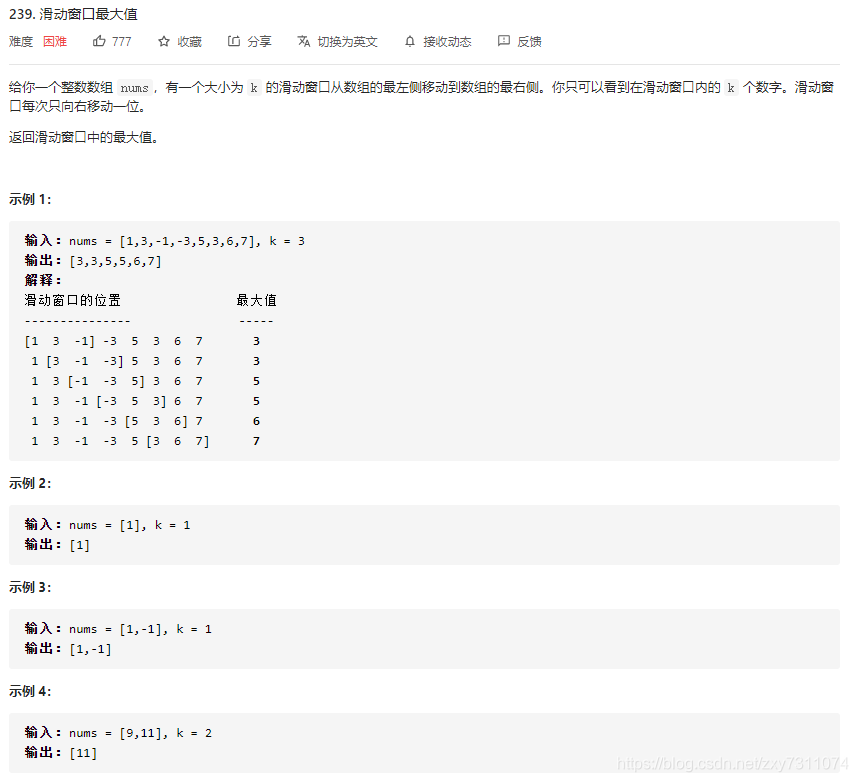
思路:
被惯性思维害死了。
一眼,哦最大的数字。要排序。再看提示,堆,滑动窗口。懂了 大根堆。
上来就直接一个大根堆,幸亏数据结构学得还行,不然直接码 真码不出来。
实现:
首先是堆得部分:
fun BuildMaxHeap(heap:IntArray, lenth:Int){//建立大根堆 顺序表存储 信息内容存储在1-n位 0号预留,用作处理
for (i in lenth/2 downTo 1 ) {//自下而上反复调整堆
HeadAdjust( heap,i,lenth)
}
}
fun HeapInsert(heap:IntArray, lenth:Int, num:Int){//往堆中插入一个数字,该题中堆的大小稳定,故直接给最后位,然后重新建堆即可
heap[lenth] = num
BuildMaxHeap( heap, lenth)
}
fun HeapOut(heap:IntArray, lenth:Int, num:Int){//从堆中删除一个数字
var templenth = lenth
var which = lenth //它在哪个位置 如果是链表存储的堆需要层次遍历
for(i in 1 until lenth){
if(heap[i] == num){
which = i
break
}
}
heap[which] = heap[lenth]//把被删除数和最后的数字调换(但并不用管被删除数
templenth --
for (j in templenth/2 downTo which) {//自下而上反复调整堆,最前面稳定的大根堆不需要调整
HeadAdjust( heap, j, templenth)
}
}
fun HeadAdjust(heap:IntArray, k :Int, lenth:Int){//自上而下调整 将元素k为根的子树进行调整
heap[0] = heap[k] //0号元素暂存子树的根节点
var root = k
var i = 2 * k
while ( i <= lenth) {//沿着较大的子节点向下筛选
if(i<lenth && heap[i] < heap[i+1]){
i++ //取较大的子节点的下标
}
if(heap[0]>=heap[i])
break; //根节点比左右孩子都大 筛选结束
else{ //孩子节点更大
heap[root] = heap[i] //交换 孩子节点和双亲节点
heap[i] = heap[0]
root = i //修改root值,以便继续向下筛选
}
i*=2
}
heap[0] = 0
}
具体大根堆得原理:
其实就是一个祖先节点比其后代节点要大的完全二叉树。
建立大根堆的时候从下往上一一调整直到任何子树调整为祖先节点都小于其后代节点。
每次插入都插在最后面,从下往上一一调整根的位置。
每次删除都和最后的元素调换位置,从下往上直到要删除的位置一一调整位置。
按照教材的说法,在建立过程中时间复杂度为O(n) 每次调整时间复杂度为O(h) 故在最好、最坏和平均情况下,堆排序的时间复杂度为O(log2n)
其次是利用大根堆实现功能:
fun maxSlidingWindow(nums: IntArray, k: Int): IntArray {
val tempArray = IntArray(k)
for (i in 0 until k) {
tempArray[i] = nums[i]
}
val heap = intArrayOf(0)+tempArray
//首先取数组前k个数据送入待处理,第一位置为0用作调整堆的临时存放
//关于为什么不生成一个新的临时变量 而采取0号位有以下好处:
//1.堆实际上是遵循了一定规则的完全二叉树,采用顺序表存储对比链表可以加快运行速度。
// 以1为开头,则其左右孩子节点分别为2,3 对应以i为长辈节点,则其左右孩子节点分别为2*i与2*i+1
// 减轻堆的处理负责度
//2.充分利用顺序表的随机读写特性,不必额外每次控制生成一个变量,减轻了开销
BuildMaxHeap( heap, k) //数组生成堆
val intarray = IntArray(nums.size-k+1)
for( i in 0 .. nums.size-k-1){
intarray[i] = heap[1]
HeapOut(heap,k,nums[i])
HeapInsert(heap,k,nums[i+k])
}
intarray[nums.size - k] = heap[1]
return intarray
}
简要过程:
就是维护大根堆,然后从大根堆读出最大值
结果:
太糟糕了,第49个实例,要求我维护大小为5W的大根堆。直接超时
反思:
再仔细想想,任何排序都需要花费较长时间。大根堆的时间复杂度已经算是比较低的了。就思路方面绝对没有问题。
回过头来就题论题,本题其实并未要求维护一个有序数组,即并不需要使用排序。况且数字的大小规定为[-10000,10000],这完全可以用hash来做这道题。
总结:
虽然没有做出题目,但是运用到的数据结构内容也是比较好的。408如果出题不可能出成这样的。感到惋惜,故留下这篇文章。
后续:
直接用hash表完成。在我看来时间复杂度的有限度远大于空间复杂度。

val Offset = 10001//偏移量为10001
fun maxSlidingWindow(nums: IntArray, k: Int) : IntArray {
val hash = IntArray(20002)
hash[0] = nums[0]//hash[0]存放当前数组的最大值
val outArray = IntArray(nums.size - k + 1)
//先对前k个数组建立hash表
for(i in 0 until k){
if(nums[i]>hash[0])
hash[0] = nums[i]
hash[nums[i]+Offset]++
}
for(i in k-1 until nums.size-1){
outArray[i-k+1] = hash[0]
addNum(hash,nums[i+1])
deleNum(hash,nums[i-k+1])
}
outArray[nums.size-k] = hash[0]
return outArray
}
fun addNum(hash :IntArray, num:Int){//增加一个num
hash[num+Offset]++
if(num>hash[0])
hash[0] = num
}
fun deleNum(hash:IntArray, num:Int){//删除一个num
hash[num+Offset]--
if(num == hash[0] && hash[num+Offset]==0){//最大值发生了变化
for(i in num-1 downTo -10000){
if(hash[i+Offset]!=0){
hash[0] = i
break
}
}
}
}

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








