Java学习day_16之API（算法，lambda）

最新推荐文章于 2025-12-03 17:03:32 发布

原创最新推荐文章于 2025-12-03 17:03:32 发布 · 916 阅读

17 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #java #学习

一、查找算法

查找算法是在一组数据（如数组、列表、数据库表等）中，快速找到目标数据（或判断目标是否存在）的方法，核心目标是提升查找效率，减少不必要的比较或遍历操作。

1.顺序查找

从数据的 “第一个” 开始，逐个与目标对比，直到找到或遍历完所有数据。

public class BasicSearchDemo {
    public static void main(String[] args) {
        //顺序查找
        //从0索引往后查找
        int[] arr = {131,127,147,81,103,23,7,79};
        System.out.println(basicSearch(arr,78));//true

    }
    public static boolean basicSearch(int[] arr,int number){
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] == number){
                return true;
            }
        }
        return false;
    }
}

2.二分查找

前提：数据必须提前按顺序排列
先找数据中间的元素，若比目标大，就只在 “左边一半” 继续找；若比目标小，就只在 “右边一半” 找，每次都排除一半数据，快速缩小范围。

public class BinarySearchDemo {
    public static void main(String[] args) {
        //二分查找
        //数组需有序，每次排除一半
        //需求：定义方法利用二分查找，查询某个元素在数组中的索引
        int[] arr = {7,23,79,81,103,127,131,147};
        System.out.println(binarySearch(arr,81));//3
    }
    public static int binarySearch(int[] arr ,int number){
        //1.定义两个变量记录要查找的范围
        int min = 0;
        int max = arr.length - 1;

        //2.利用循环不断的去找要查找的数据
        while(true){
            if (min > max){
                return -1;
            }
            //3.找到min和max的中间位置
            int mid = (min + max) / 2;
            if (arr[mid] > number){
                max = mid - 1;
            }else if (arr[mid] < number){
                min = mid + 1;
            }
            else {
                return mid;
            }
        }
    }
}

3.分块查找

基本思路：
1.数据分块：

将无序数据划分为若干块（子表）
块内数据可以无序，但块之间必须有序（即前一块的最大元素小于后一块的最小元素）

2.建立索引表：

为每个块创建索引项，包含块的最大元素值和块的起始位置
索引表本身是有序的

3.查找过程：

先在索引表中查找（可用二分查找），确定目标可能所在的块
再在对应块内进行顺序查找

public class BlockSearch {
    public static void main(String[] args) {
        /*
        分块查找
        块内无序，块间有序
        实现步骤
            1.创建数组blockArr存放每一个块对象的信息
            2.先查找blockArr确定要查找的数据属于哪一块
            3.再单独遍历这一块数据即可
         */
        int[] arr = {16,5,9,12,21,18,
                32,23,37,26,45,34,
                50,48,61,52,73,66
        };
        //创建三个块的对象
        Block b1 = new Block(21,0,5);
        Block b2 = new Block(45,6,11);
        Block b3 = new Block(73,12,17);

        //定义数组用来管理三个块的对象（索引表）
        Block[] blockArr = {b1,b2,b3};

        //定义一个变量用来记录要查找的元素
        int number = 37;

        //调用方法：传递索引表，数组，要查找的元素
        int index = getIndex(blockArr,arr,number);
        System.out.println(index);//8
    }

    //利用分块查找的原理，查询number的索引
    private static int getIndex(Block[] blockArr, int[] arr, int number) {
        //1.确定number是在哪一块当中
        int indexBlock = findIndexBlock(blockArr,number);
        if (indexBlock == -1){
            //表示number不在数组当中
            return -1;
        }
        //2.获取这一块的起始索引和结束索引
        int startIndex = blockArr[indexBlock].getStartIndex();
        int endIndex = blockArr[indexBlock].getEndIndex();
        //3.遍历
        for (int i = startIndex;i <= endIndex; i++){
            if (arr[i] == number){
                return i;
            }
        }
        return -1;
    }
    //定义一个方法，用来确定number在哪一块中
    public static int findIndexBlock(Block[] blockArr,int number){
        //从0索引开始遍历blockArr，如果number小于等于max，那么就表示number是在这一块当中的
        for (int i = 0; i < blockArr.length; i++) {
            if (number <= blockArr[i].getMax()){
                return i;
            }
        }
        return -1;
    }
}

class Block{
    private int max;
    private int startIndex;
    private int endIndex;

    public Block() {
    }

    public Block(int max, int startIndex, int endIndex) {
        this.max = max;
        this.startIndex = startIndex;
        this.endIndex = endIndex;
    }

    public int getMax() {
        return max;
    }

    public void setMax(int max) {
        this.max = max;
    }

    public int getStartIndex() {
        return startIndex;
    }

    public void setStartIndex(int startIndex) {
        this.startIndex = startIndex;
    }

    public int getEndIndex() {
        return endIndex;
    }

    public void setEndIndex(int endIndex) {
        this.endIndex = endIndex;
    }
}

二、排序算法

排序算法是将一组数据（例如一个数组或列表）中的元素按照某种特定的顺序（通常是数字大小或字典序）进行重新排列的算法。

1.冒泡排序

思想：重复地“遍历”待排序的列表，依次比较相邻的两个元素，如果它们的顺序错误就把它们交换过来。遍历列表的工作会重复进行，直到没有再需要交换的元素为止。

public class BubbleDemo {
    public static void main(String[] args) {

        //1.定义数组
        int[] arr = {3,2,5,8,4,9};

        for (int i = 0; i < arr.length -1 ; i++) {
            for (int j = 0; j < arr.length - 1 - i; j++){
                if (arr[j] > arr[j + 1]){
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }

        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i] + " ");//2 3 4 5 8 9 
        }
    }
}

2.选择排序

首先在未排序序列中找到最小（或最大）元素，存放到排序序列的起始位置。然后，再从剩余未排序元素中继续寻找最小（或最大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

public class SelectionDemo {
    public static void main(String[] args) {
        int[] arr = {3,2,5,8,4,9};

        for (int i = 0; i < arr.length - 1; i++) {
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[i] > arr[j]){
                    int temp = arr[i];
                    arr[i] = arr[j];
                    arr[j] = temp;
                }
            }
        }
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i] + " ");//2 3 4 5 8 9
        }
    }
}

3.插入排序

将待排序序列分为 “已排序部分” 和 “未排序部分”，每次从 “未排序部分” 取出第一个元素，将其插入到 “已排序部分” 中合适的位置，使 “已排序部分” 始终保持有序，重复此过程直至所有元素完成插入

public class InsertDemo {
    public static void main(String[] args) {
        int[] arr = {3,44,38,5,47,15,36,26,27,2,46,4,19,50,48};
        //1.找到无序的那一组是从哪个索引开始的
        int startIndex = -1;
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] > arr[i+1]){
                startIndex = i + 1;
                break;
            }
        }
        //2.遍历从startIndex开始到最后一个元素，依次得到无序的那一组数据中的每一个元素
        for (int i = startIndex; i < arr.length; i++) {
            //记录当前要插入数据的索引
            int j = i;
            while (j > 0 && arr[j] < arr[j -1]){
                //交换位置
                int temp = arr[j];
                arr[j] = arr[j - 1];
                arr[j - 1] = temp;
                j--;
            }
        }
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i] + " ");
        }
    }
}

4.快速排序

核心思想

选择基准：从待排序序列中选择一个元素作为 “基准”（pivot）。
分区操作：将序列中所有比基准小的元素移到基准左侧，比基准大的元素移到基准右侧（相等元素可放任意一侧），此时基准元素的位置已确定（即最终排序后的位置）。
递归排序：对基准左侧和右侧的两个子序列分别重复上述步骤（选择基准、分区），直到子序列长度为 0 或 1（天然有序）。

public class QuickDemo {
    public static void main(String[] args) {
        int[] arr = {6,1,2,7,9,3,4,5,10,8};
        quickSort(arr,0,arr.length - 1);
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i] + " ");
        }
    }

    private static void quickSort(int[] arr, int i, int j) {
        //定义两个变量记录要查找的范围
        int start = i;
        int end = j;
        if (start > end){
            //递归的出口
            return;
        }

        //记录基准数
        int baseNumber = arr[i];
        //利用循环找到要交换的数字
        while (start != end){
            //利用end，从后往前开始找，找比基准数小的数字
            while (true){
                if (end <= start || arr[end] < baseNumber){
                    break;
                }
                end--;
            }
            //利用start，从前往后找，找比基准数大的数字
            while (true){
                if (end <= start || arr[start] > baseNumber){
                    break;
                }
                start++;
            }
            //把end和start指向的元素进行交换
            int temp = arr[start];
            arr[start] = arr[end];
            arr[end] = temp;
        }
        //当start和end指向了同一个元素的时候，那么上面的循环就会结束
        //表示已经找到了基准数在数组中应存入的位置
        //基准数归位
        //拿着这个范围的第一个数字，跟start指向的元素进行交换
        int temp = arr[i];
        arr[i] = arr[start];
        arr[start] = temp;

        //确定基准数左边的范围，重复刚刚所作的事情
        quickSort(arr,i,start - 1);
        //确定基准数右边的范围，重复刚刚所作的事情
        quickSort(arr,start + 1,j);
    }
}

三、Arrays

专门用于操作数组提供了一系列静态方法来实现数组的排序、查找、填充、比较、转换等常见操作。

方法名	说明
public static String toString(数组)	把数组拼接成一个字符串
public static int binarySearch(数组，查找的元素)	二分查找法查找元素
public static int[] copyOf(原数组，新数组长度)	拷贝数组
public static int[] copyOfRange(原数组，起始索引，结束索引)	拷贝数组（指定范围）
public static void fill(数组，元素)	填充数组
public static void sort(数组)	按照默认方式进行数组排序
public static void sort(数组，排序规则)	按照指定的规则排序

import java.util.Arrays;

public class ArraysDemo {
    public static void main(String[] args) {
        //toString：将数组变成字符串
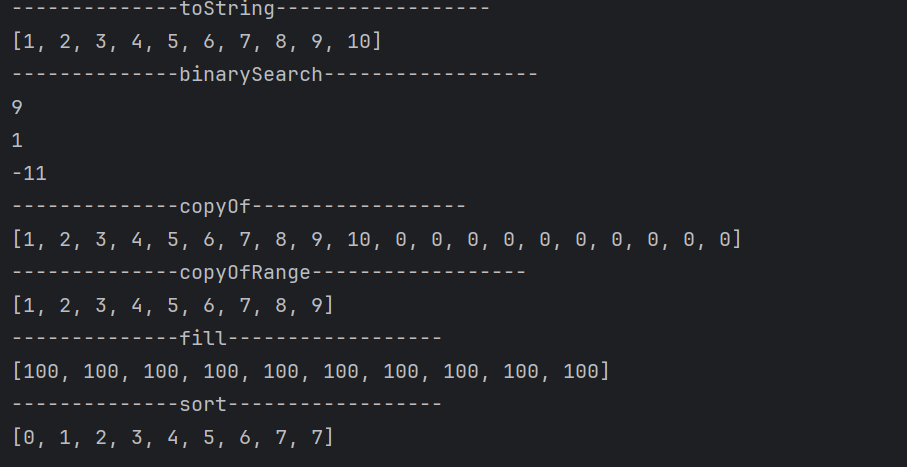
        System.out.println("--------------toString------------------");
        int[] arr = {1,2,3,4,5,6,7,8,9,10};
        System.out.println(Arrays.toString(arr));

        //binarySearch:二分查找法查找元素
        //数组元素必须升序
        //插入元素不存在，返回-插入点 -1 -10 -1
        System.out.println("--------------binarySearch------------------");
        System.out.println(Arrays.binarySearch(arr,10));
        System.out.println(Arrays.binarySearch(arr,2));
        System.out.println(Arrays.binarySearch(arr,20));

        //copyOf：拷贝数组;
        System.out.println("--------------copyOf------------------");
        int[] newArr1 = Arrays.copyOf(arr,20);
        System.out.println(Arrays.toString(newArr1));

        //copyOfRange:拷贝数组（指定范围）
        //包头不包尾，包左不包右
        System.out.println("--------------copyOfRange------------------");
        int[] newArr2 = Arrays.copyOfRange(arr,0,9);
        System.out.println(Arrays.toString(newArr2));

        //fill：填充数组
        System.out.println("--------------fill------------------");
        Arrays.fill(arr,100);
        System.out.println(Arrays.toString(arr));

        //sort:排序。默认情况下，给基本数据类型进行升序排列(快速排序)
        System.out.println("--------------sort------------------");
        int[] arr2 = {4,1,5,7,2,0,3,7,6};
        Arrays.sort(arr2);
        System.out.println(Arrays.toString(arr2));
    }
}

在这里插入图片描述

四、lambda表达式

Lambda 表达式本质是一种匿名函数的简洁语法，核心作用是将 “一段逻辑（行为）” 像参数一样传递给方法，无需定义完整的匿名内部类。它解决了传统 Java 中 “为了传递一段简单逻辑，必须编写冗余匿名内部类” 的问题，让代码更聚焦于 “要实现的逻辑”，而非 “语法模板”。

Lambda 表达式不能独立使用，必须与函数式接口配合，这是其语法生效的核心前提。
函数式接口：
接口中仅有一个抽象方法
可通过 @FunctionalInterface 注解显式标记

public class LambdaDemo {
    public static void main(String[] args) {

        method(
                ()->{
                    System.out.println("游泳");
                }
        );
    }
    public static void method(Swim s){
        s.swimming();
    }
}
interface Swim{
    public abstract void swimming();
}

lambda省略规则
1.参数类型可以省略不写
2.如果只有一个参数，参数类型可以省略，同时（）也可以省略
3.如果Lambda表达式的方法体只有一行，大括号，分号，return可以省略不写，需要同时省略

public class LambdaDemo2 {
    public static void main(String[] args) {
        /*
        lambda省略规则
            1.参数类型可以省略不写
            2.如果只有一个参数，参数类型可以省略，同时（）也可以省略
            3.如果Lambda表达式的方法体只有一行，大括号，分号，return可以省略不写，需要同时省略
         */
        Integer[] arr = {9,8,7,6,5,4,3,2,1};

//        Arrays.sort(arr, new Comparator<Integer>() {
//            @Override
//            public int compare(Integer o1, Integer o2) {
//                return o1 - o2;
//            }
//        });
//        //lambda完整格式
//        Arrays.sort(arr, (Integer o1, Integer o2) -> {
//                return o1 -o2;
//            }
//        );
        //lambda省略格式
        Arrays.sort(arr,(o1,o2) -> o1 - o2);
        System.out.println(Arrays.toString(arr));
    }
}