问题 A: 关键路径

题目描述
描述：
图的连接边上的数据表示其权值，带权值的图称作网。

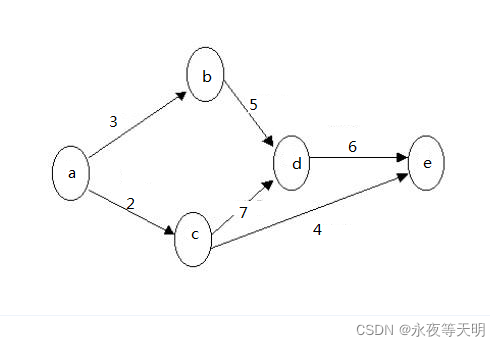
上图可描述为顶点集为（a,b,c,d,e)
边集及其权值为(始点，终点 权值）：
a b 3
a c 2
b d 5
c d 7
c e 4
d e 6

网的源点是入度为0的顶点，汇点是出度为0的顶点。网的关键路径是指从源点到汇点的所有路径中，具有最大路径长度的路径。上图中的关键路径为a->c->d->e，其权值之和为关键路径的长度为15。

本题的要求是根据给出的网的邻接矩阵求该网的关键路径及其长度。

输入
第一行输入一个正整数n（1<=n<=5)，其代表测试数据数目，即图的数目
第二行输入x(1<=x<=15)代表顶点个数，y(1<=y<=19)代表边的条数
第三行给出图中的顶点集，共x个小写字母表示顶点
接下来每行给出一条边的始点和终点及其权值，用空格相隔，每行代表一条边。

输出
第一个输出是图的关键路径（用给出的字母表示顶点， 用括号将边括起来，顶点逗号相隔）
第二个输出是关键路径的长度
每个矩阵对应上面两个输出，两个输出在同一行用空格间隔，每个矩阵的输出占一行。

样例输入

2
5 6
abcde
a b 3
a c 2
b d 5
c d 7
c e 4
d e 6
4 5
abcd
a b 2
a c 3
a d 4
b d 1
c d 3

样例输出

(a,c) (c,d) (d,e) 15
(a,c) (c,d) 6

提示
作者：梁青青

思路：使用map建立字母与数字的映射，新建一个邻接表用于保存关键活动。

#include <cstdio>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <cstring>
#include <algorithm>
using namespace std;

const int MAXV = 110;

struct Node {
    int v, dis;
    Node(int _v, int _dis) :
        //构造函数
        v(_v), dis(_dis){};
};
vector<Node> Adj[MAXV]; //邻接表
vector<int> ans[MAXV];
int n, m, inDegree[MAXV];
int ve[MAXV], vl[MAXV];
char str[MAXV];
map<char, int> mp;

//拓扑序列
stack<int> topOrder;
//拓扑排序
bool topologicalSort() {
    memset(ve, 0, sizeof(ve));
    queue<int> q;
    for (int i = 0; i < n; i++) {
        if (inDegree[i] == 0) {
            q.push(i); //将所有入度为0的顶点入队
        }
    }
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        topOrder.push(u);
        for (int i = 0; i < Adj[u].size(); i++) {
            int v = Adj[u][i].v; // u的后继结点v
            inDegree[v]--;
            if (inDegree[v] == 0) {
                q.push(v);
            }
            //用ve[u]来更新u的所有后继结点v
            if (ve[u] + Adj[u][i].dis > ve[v]) {
                ve[v] = ve[u] + Adj[u][i].dis;
            }
        }
    }
    if (topOrder.size() == n) {
        return true;
    } else {
        return false;
    }
}

int criticalPath() {
    memset(ve, 0, sizeof(ve));
    if (topologicalSort() == false) {
        return -1;
    }
    int maxLength = 0;
    for (int i = 0; i < n; i++) {
        maxLength = ve[i];
    }
    fill(vl, vl + n, maxLength);

    //直接使用topOrder出栈即为逆拓扑序列，求解vl数组
    while (!topOrder.empty()) {
        int u = topOrder.top();
        topOrder.pop();
        for (int i = 0; i < Adj[u].size(); i++) {
            int v = Adj[u][i].v; // u的后继结点
            //用u的所有后继结点v的vl值来更新vl[u]
            if (vl[v] - Adj[u][i].dis < vl[u]) {
                vl[u] = vl[v] - Adj[u][i].dis;
            }
        }
    }
    for (int i = 0; i < n; ++i) ans[i].clear();

    //遍历邻接表的所有边，计算活动的最早开始时间e和最迟开始时间l
    for (int u = 0; u < n; u++) {
        for (int i = 0; i < Adj[u].size(); i++) {
            int v = Adj[u][i].v, dis = Adj[u][i].dis;
            //活动最早开始时间e和最迟开始时间l
            int e = ve[u], l = vl[v] - dis;
            //如果e==l，说明活动u->v是关键活动
            if (e == l) {
                ans[u].push_back(v);
            }
        }
    }
    int s; //源点
    for (int i = 0; i < n; ++i) {
        if (ve[i] == 0) {
            s = i;
            break;
        }
    }
    while (!ans[s].empty()) {
        printf("(%c,%c) ", str[s], str[ans[s][0]]);
        s = ans[s][0]; // s的后继结点
    }
    return maxLength; //返回关键路径长度
}

int main() {
    int k, dis;
    char a, b;
    while (scanf("%d", &k) != EOF) {
        while (k--) {
            for (int i = 0; i < n; i++) Adj[i].clear();
            memset(inDegree, 0, sizeof(inDegree));
            mp.clear();
            scanf("%d %d", &n, &m);
            scanf("%s", str);
            for (int i = 0; i < n; i++) {
                mp[str[i]] = i;
            }
            for (int j = 0; j < m; ++j) {
                getchar();
                scanf("%c %c %d", &a, &b, &dis);
                Adj[mp[a]].push_back(Node(mp[b], dis));
                inDegree[mp[b]]++;
            }
            int length = criticalPath();
            printf("%d\n", length);
        }
    }
    return 0;
}