五、理论讲解:数组和链表

数组:
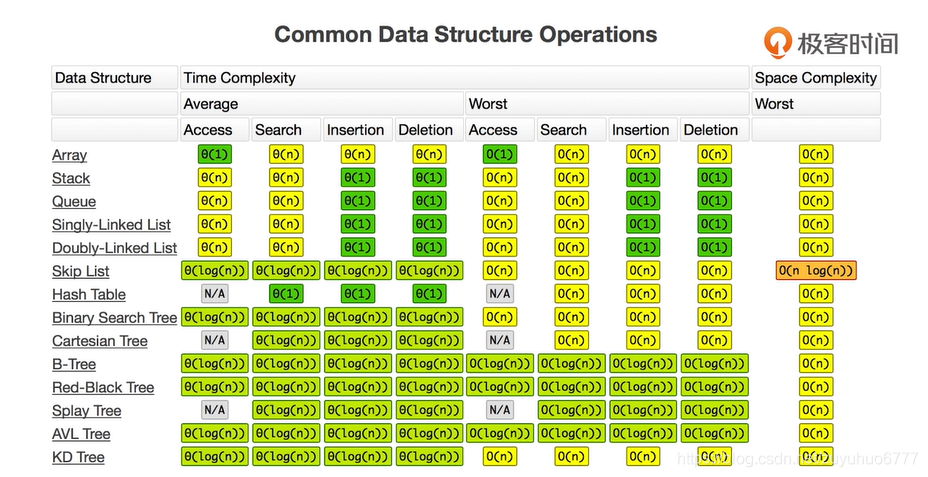
1、访问:O(1)
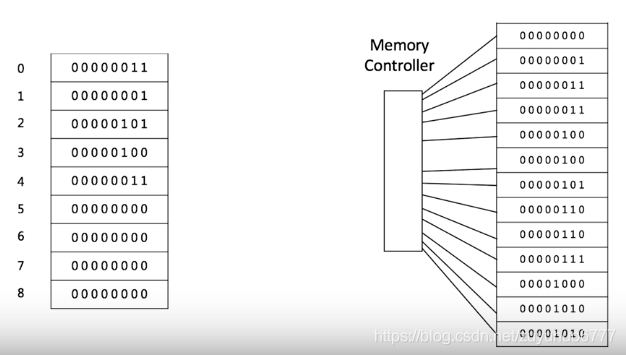
2、插入和删除:时间复杂度:0(n)
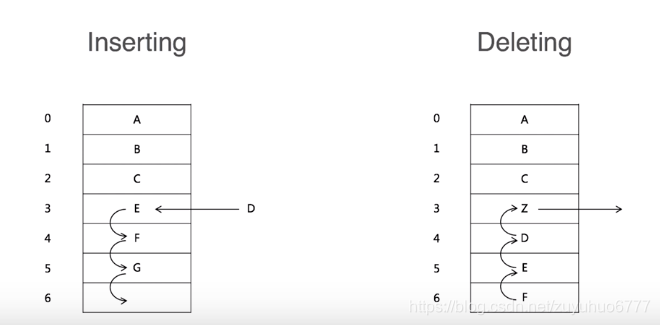
链表

插入和删除是o(1)
查找是o(n)的

六:反转一个单链表和判断链表是否有坏
1、反转链表:
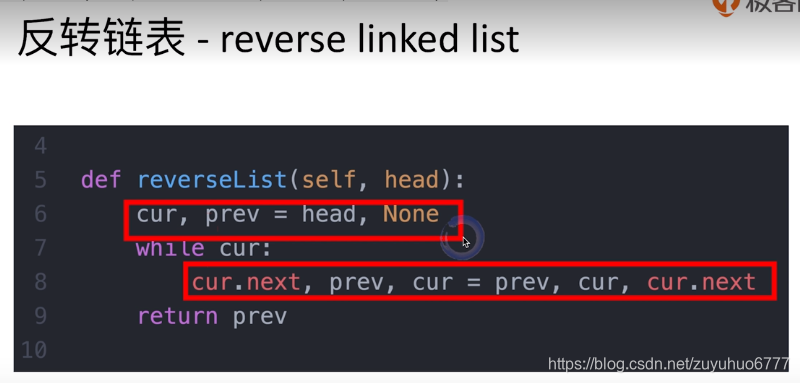
2、反转相邻的
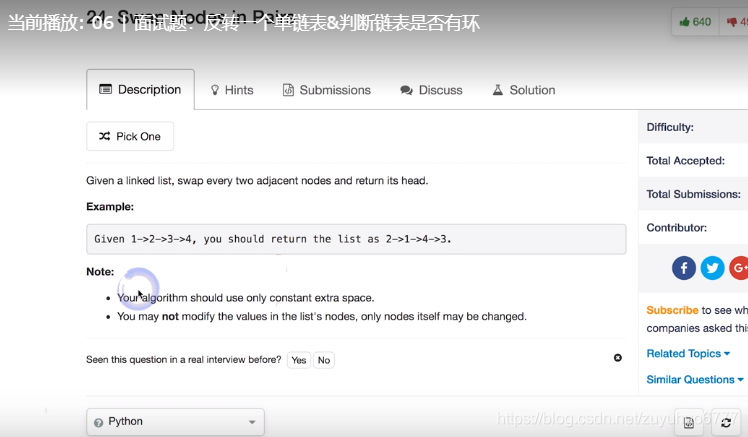
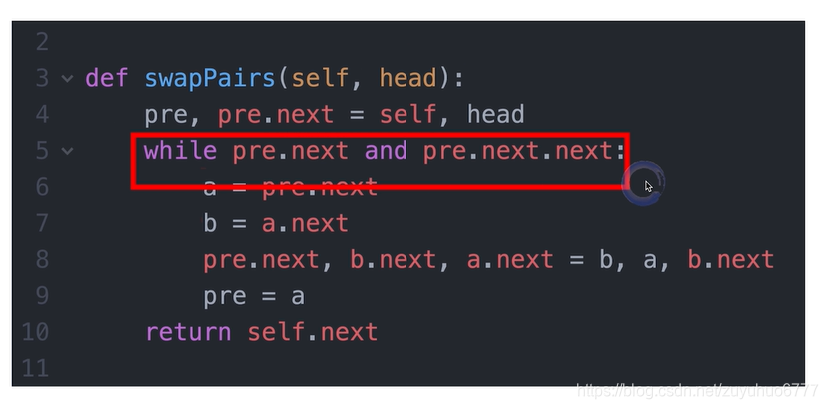
解释:1、作者是想把 self 当做链表的头指针使用的(注意:头指针 pHead 与传入的参数 head 是不同的,head 是第一个结点)最后只要返回 self.next 就得到了答案。
3、给定一个链表,判断中间是否有环
1、硬做(直接判断,有没有none)
2、set(判重) o(n)
3、快慢指针的解法

对于为什么快慢指针会相遇,做了一些思考:
首先两者要相遇,肯定是在那个环里面(比如最好情况慢的指针一踏入环就和快指针相遇)。
然后我们要明确快慢指针的速度差为1,两者每移动一下,距离减1,而这个环的最小划分单位就是1,所以显然会相遇。
七、理论讲解:栈和队列
栈:先入后出
队列:先入先出
八、判断括号字符串是否有效
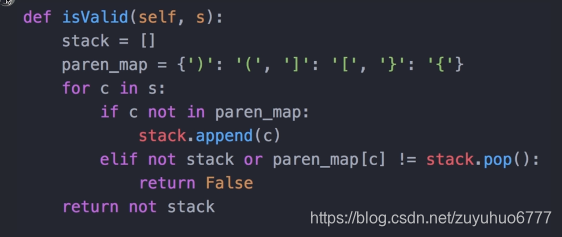
if 判断,如果在了,就直接False
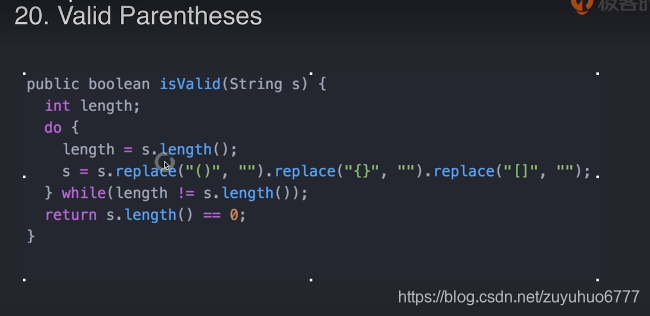
上面这个思路,他的时间复杂度很高,
replace本身的操作是 o(n) 的,所以最坏情况下会有产生 n^2 的复杂度
九、用队列实现栈,用栈实现队列
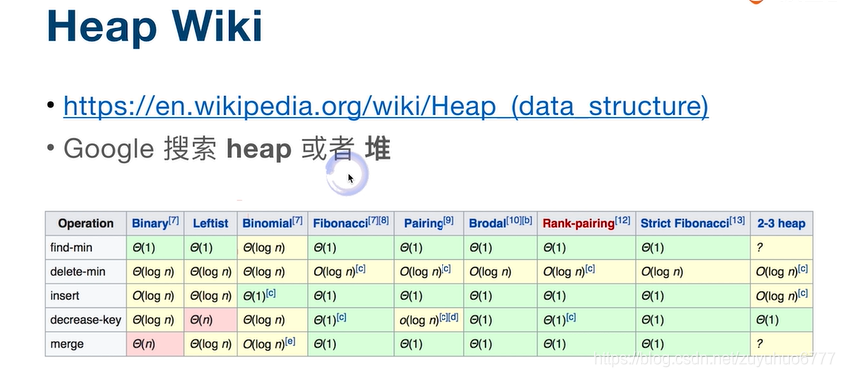
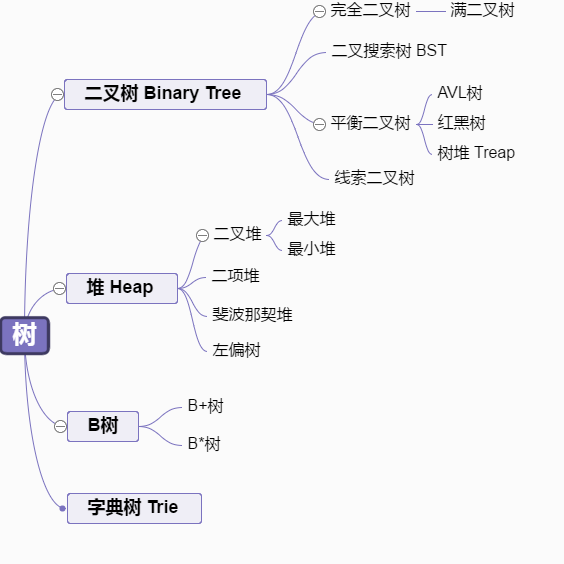
十、优先队列


堆和二叉搜素树来实现
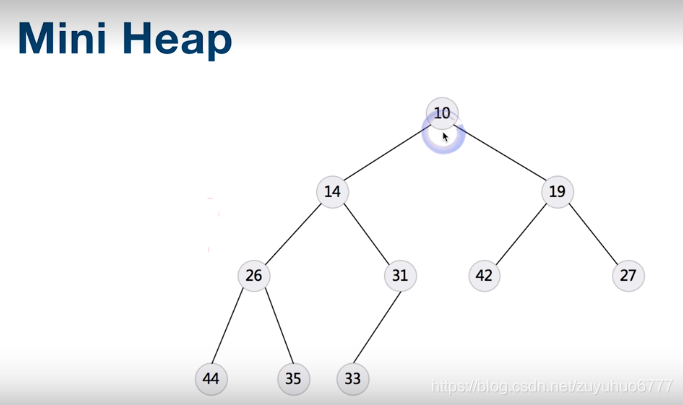
小顶堆为例
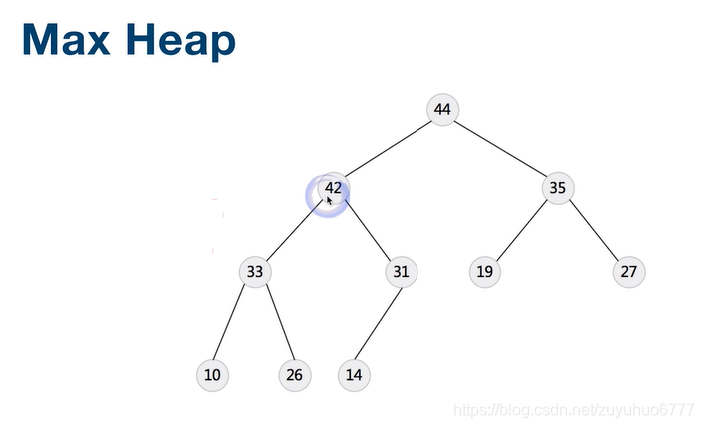
大顶堆
十一、返回数据流中的第K大元素
1、保存前k个最大值,再排序(N*k*log(k))
2、优先队列指的是每次把最大的元素放在最上面或者最小的元素放在最上面
维护一个min heap(小顶堆) (包含K个值)(N*1*1og2K)
java:

python
class KthLargest(object):
def __init__(self, k, nums):
"""
:type k: int
:type nums: List[int]
"""
self.pool = nums
self.size = len(self.pool)
self.k = k
heapq.heapify(self.pool)
while self.size > k:
heapq.heappop(self.pool)
self.size -= 1
def add(self, val):
"""
:type val: int
:rtype: int
"""
if self.size < self.k:
heapq.heappush(self.pool, val)
self.size += 1
elif val > self.pool[0]:
heapq.heapreplace(self.pool, val)
return self.pool[0]
#
#heap = [] #创建了一个空堆
#heappush(heap,item) #往堆中插入一条新的值
#item = heappop(heap) #从堆中弹出最小值
#item = heap[0] #查看堆中最小值,不弹出
#heapify(x) #以线性时间讲一个列表转化为堆
#item = heapreplace(heap,item) #弹出并返回最小值,然后将heapqreplace方法中item的值插入到堆#
##中,堆的整体结构不会发生改变。这里需要考虑到的情况就是如果弹出的值大于item的时候我们可能就需要
#添加条件来满足function的要求
参考:https://blog.youkuaiyun.com/minxihou/article/details/51857518
十二 返回滑动窗口的最大值
1、优先队列的方法(大顶堆)
a.维护HAEP 复杂度:logk
b-max-TOP
N*logk
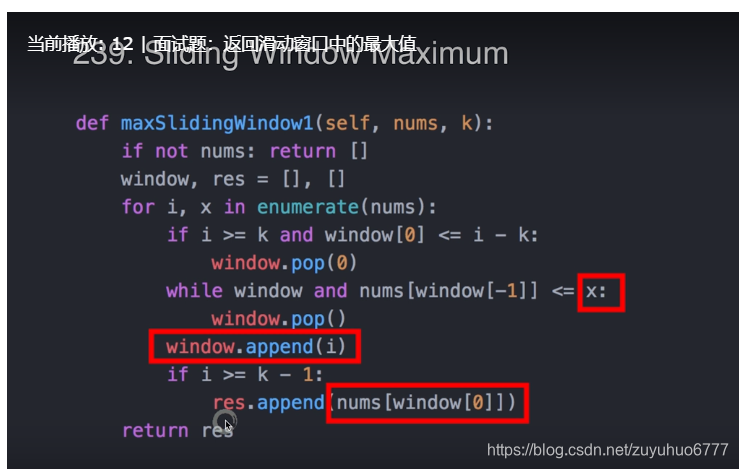
2、双端队列D-Queue ,用数组实现就可以 题目特点:窗口固定,且只要最大值,不需要维护其他值,所以双端队列的方法会优于
优先队列
a、入队列
b、维护(最大值永远都是最左边的值)
N*O(1)=o(n)
双端队列的写法:
 数据结构与算法精讲
数据结构与算法精讲





 本文深入探讨了数据结构如数组、链表、栈、队列及优先队列的特性与应用,解析了典型算法问题如括号字符串验证、滑动窗口最大值的解决方案,并介绍了如何使用队列实现栈,反之亦然。
本文深入探讨了数据结构如数组、链表、栈、队列及优先队列的特性与应用,解析了典型算法问题如括号字符串验证、滑动窗口最大值的解决方案,并介绍了如何使用队列实现栈,反之亦然。
















 6275
6275

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








