数据结构实验(C++)
PS:仅数据结构实验记录
题目:创建设计一个算法,将一般算术表达式转化为逆波兰表达式,并求逆波兰表达式的值。
#include<iostream>
using namespace std;
const int Max_size = 30;
char result[30];
char num;
//创建一个栈
class Seqlist
{
public:
char data[Max_size];
int top;
Seqlist() //构造函数
{
top = -1;
}
~Seqlist() {} //析构函数
char Pop() //入栈操作
{
char x;
if (top == -1)
{
cout<<"下溢" << endl;
exit(0);
}
x = data[top];
top--;
return x;
}
void Push(char x) //出栈操作
{
if (top == Max_size - 1)
{
cout << "上溢" << endl;
exit(0);
}
else
{
top++;
data[top] = x;
}
}
bool Empty() //判空操作
{
if (top == -1)
return 1;
return 0;
}
char GetTop() //取栈顶元素(并不删除)
{
if (top != -1)
return data[top];
return 0;
}
};
//判断提取字符是否为数字,是的话返回1,否则返回0
bool isNumber(char op)
{
switch (op)
{
case ' ':
case '(':
case ')':
case '+':
case '-':
case '*':
case '/':
case '#':
return 0;
default:
return 1;
}
}
//判断操作符的优先级
int prior(char ch)
{
int value = 10;
switch(ch)
{
case '(':
value = 4;
break;
case ')':
value = 4;
break;
case '*':
value = 2;
break;
case '/':
value = 2;
break;
case '+':
value = 3;
break;
case '-':
value = 3;
break;
case '#':
value = 5;
break;
default:
break;
}
return value;
}
//将波兰式改成逆波兰式
void change(char arr[])
{
Seqlist SE; //创建栈
int i = 0; //遍历公式下标
char ch;
for (i = 0; arr[i] != '\0'; i++)
{
if (isNumber(arr[i])) //判断是否为数字
{
result[num++] = arr[i];
}
else
{
if (SE.Empty() || arr[i] == '(') //队列为空或字符为‘(’时入栈
{
SE.Push(arr[i]);
continue;
}
if (arr[i] == '#') //为#时结束
break;
if (arr[i] == ')') //为‘)’时
{
result[num++] = ' ';
while ((ch = SE.Pop()) != '(')
{
result[num++] = ch;
result[num++] = ' ';
}
continue;
}
result[num++] = ' ';
ch = (prior(SE.GetTop()))- (prior(arr[i])); //判断操作符优先级
if (ch > 0) //操作符优先,入栈
{
SE.Push(arr[i]);
}
else if (ch <= 0) //操作符较小时,出栈
{
while (prior(arr[i] >= prior(SE.GetTop())))
{
printf("%c", ch = SE.Pop());
result[num++] = SE.Pop();
printf(" ");
result[num++] = ' ';
}
SE.Push(arr[i]);
}
}
}
while (SE.GetTop() != '#')
{
result[num++] = ' ';
result[num++] = SE.Pop();
}
for (i = 0; i < num; i++)
printf("%c", result[i]);
}
//计算值
int Cal_(char arr[])
{
int i, cal[10], top = -1;
memset(cal, 0, sizeof(cal));
for (i = 0; i < num; i++)
{
if (isNumber(arr[i]))
{
top++;
while (arr[i] != ' ')//获取一个整数,并入栈
{
cal[top] = cal[top] * 10 + arr[i++] - 48;
}
}
else
{
switch (arr[i])
{
//模拟出栈
case '+':
cal[top - 1] = cal[top - 1] + cal[top];
cal[top--] = 0;
break;
case '-':
cal[top - 1] = cal[top - 1] - cal[top];
cal[top--] = 0;
break;
case '*':
cal[top - 1] = cal[top - 1] * cal[top];
cal[top--] = 0;
break;
case '/':
cal[top - 1] = cal[top - 1] / cal[top];
cal[top--] = 0;
break;
default:
break;
}
}
}
return cal[0];
}
//测试
int main()
{
char test[] = "#(1+2)*4#";
printf("算术表达式:");
printf("%s\n", test);
printf("逆波兰表达式:");
change(test);
printf("\n");
printf("运算结果为:%d\n", Cal_(result));
return 0;
}
测试结果
本次实验测试了两组数据分别是:
(1)#(1+2)4#,算术表达式中含所有括号,则其逆波兰表达式应为:1 2 + 4 * ,结果为:12;实验结果如图:
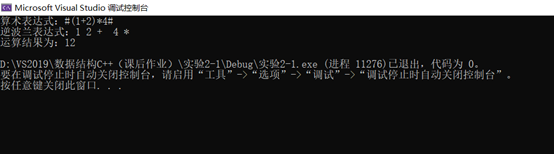
(2)#20-33#,算术表达式中不包含括号,则其逆波兰表达式应为:20 3 3 * - ,结果为:11;
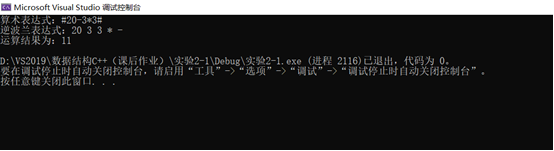








 本文介绍了如何使用C++编程实现逆波兰表达式(RPN)的转换,从一般算术表达式到逆波兰表达式,并通过栈数据结构进行计算。实验涉及括号处理、操作符优先级判断、数字识别等关键步骤,最终得出表达式的计算结果。测试案例包括带括号和不带括号的表达式,验证了算法的正确性。
本文介绍了如何使用C++编程实现逆波兰表达式(RPN)的转换,从一般算术表达式到逆波兰表达式,并通过栈数据结构进行计算。实验涉及括号处理、操作符优先级判断、数字识别等关键步骤,最终得出表达式的计算结果。测试案例包括带括号和不带括号的表达式,验证了算法的正确性。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








