数据结构 二叉树(1)二叉树简单了解

于 2025-08-06 22:19:21 发布
阅读量534 收藏 5
点赞数 14
CC 4.0 BY-SA版权
文章标签： 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/ztztz111/article/details/149981295

二叉树

1. 树概念及结构

1.1 树的概念

树的定义：

  • 树是非线性数据结构，由 n（n≥0） 个有限结点组成，结点间通过层次关系组织。
  • 形态特征：形似“倒挂的树”，根朝上、叶朝下，是递归定义的结构（子树也符合树的定义）。

根结点特性：

  • 树有且仅有一个根结点（n=0 时为空树，无结点；n>0 时根结点唯一）。
  • 根结点无“前驱结点”，是整棵树的起点。
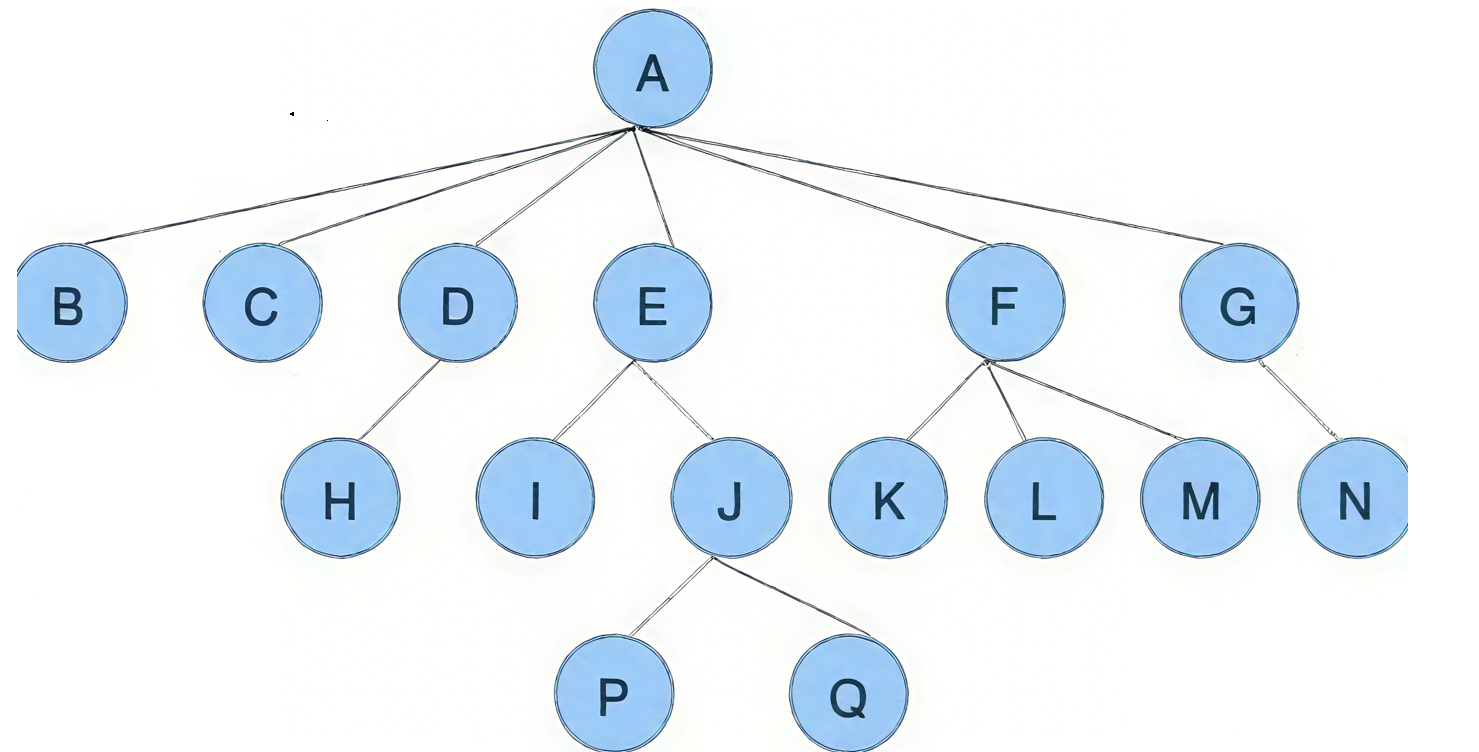
    在这里插入图片描述

子树规则：

  • 除根外，其余结点被划分为 M（M>0） 个互不相交的子集，每个子集是一棵“子树”。
  • 子树的根结点：有且仅有 1 个前驱（即父结点），但可含 0 或多个后继（子结点）。
  • 核心约束：子树间绝对不能相交，否则破坏树形结构的层次独立性。
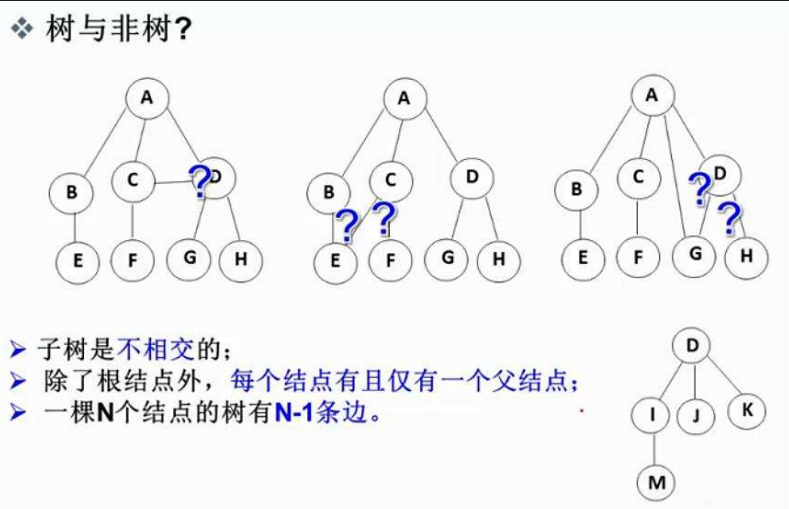
    在这里插入图片描述
  • 在树形结构中不会存在回路 所以上图的第一二三个结构都不是树，存在回路结构的数据结构是后期会学的图。

1.2 树的相关概念

在这里插入图片描述

  1. 节点的度：

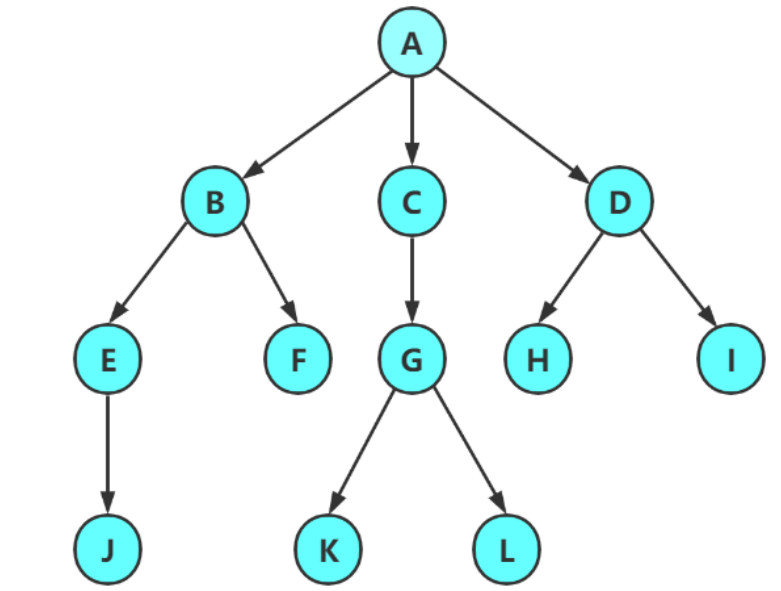
    • 定义：一个节点包含的子树数量（即直接子结点的个数）。
    • 示例（对应图）：A 的度是 6（直接子结点 B、C、D、E、F、G 共 6 个）。

  2. 叶节点（终端节点）：

    • 定义：度为 0 的节点（无直接子结点，是树的“末端”）。
    • 示例（对应图）：B、C、H、I、K、L、M、N、P、Q 等（无分支延伸）。

  3. 非终端节点（分支节点）：

    • 定义：度≠0 的节点（有直接子结点，处于树的“中间层”）。
    • 示例（对应图）：D（子结点 H）、E（子结点 I、J）、F（子结点 K、L、M、N）、G（无？不，G 无子结点？哦图中 G 可能无子结点？重新看：原树中 G 若无子结点则是叶节点？需修正：假设图中 G 无子结点则是叶节点，分支节点应为 D、E、F 等。需严格按图判断：D 有子 H，E 有子 I、J，F 有子 K、L、M、N，所以 D、E、F 是分支节点；A 度 6，也是分支节点）。

  4. 双亲节点（父节点）：

    • 定义：若节点 有子结点，则称其为子结点的“父节点”。
    • 示例（对应图）：A 是 B、C、D、E、F、G 的父节点；D 是 H 的父节点；E 是 I、J 的父节点 。

  5. 孩子节点（子节点）：

    • 定义：节点的子树根结点（即直接子结点）。
    • 示例（对应图）：B、C、D、E、F、G 是 A 的孩子节点；H 是 D 的孩子节点 。

  6. 树的度：

    • 定义：整棵树中最大的节点的度（反映树的“分支密集程度”）。
    • 示例（对应图）：A 的度是 6，其他节点度更小（如 D 度 1，E 度 2 等），因此树的度为 6 。

  7. 节点的层次：

    • 定义：从根开始计数，根为第 1 层，根的子结点为第 2 层，依此类推（体现节点的“深度位置”）。
    • 示例（对应图）：
      • A 在第 1 层；
      • B、C、D、E、F、G 在第 2 层；
      • H（D 的子）、I（E 的子）、J（E 的子）、K（F 的子）、L（F 的子）、M（F 的子）、N（F 的子）在第 3 层；
      • P（J 的子）、Q（J 的子）在第 4 层 。

  8. 树的高度（深度）：

    • 定义：树中节点的最大层次（反映树的“纵向规模”）。
    • 示例（对应图）：最大层次是 4（P、Q 所在层），因此树的高度为 4 。

  9. 森林：

    • 定义：由 m（m>0） 棵互不相交的树组成的集合（可理解为“多棵独立树的组合”）。
    • 示例：若把原树拆分为 3 棵独立树（如 A 为根的树拆成 B、C 单独成树，其余成另一棵），则这 3 棵树构成森林（需保证子树不相交）。

1.3 树的表示

树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了，既然保存值域，也要保存结点和结点之间的关系，实际中树有很多种表示方式如：双亲表示法，孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。

1.3.1 双亲表示法

双亲表示法：

  • 核心思路：用数组存储树中节点，每个节点额外记录其“父节点在数组中的下标”，通过父节点索引维护节点间的层次关系。

  • 结构定义（伪代码）：

    #define MAX_NODE 100
typedef struct {
    DataType _data;       // 节点数据域
    int _parentIndex;     // 父节点在数组中的下标，根节点可设为 -1
} ParentTreeNode;
ParentTreeNode tree[MAX_NODE];

  • 示例（结合类似逻辑，假设图中节点用数组存储）：
    若根节点 A 是数组第 0 号元素，tree[0]._parentIndex = -1；
    节点 B 是 A 的子节点，存于数组第 1 号，tree[1]._parentIndex = 0 ，以此类推。

  • 优缺点：
    优点：找父节点极快（直接通过下标访问），适合频繁查询父节点的场景。
    缺点：找子节点需遍历整个数组（逐个检查 _parentIndex），效率低；删除节点时需处理子节点 “认父” 问题，逻辑复杂。
    在这里插入图片描述

1.3.2 孩子表示法

孩子表示法：

  • 核心思路：用数组存节点，每个节点通过链表/数组存储其所有“子节点的索引/指针”，聚焦子节点关系的维护。
  • 结构定义（伪代码，链表版）：
    typedef struct ChildNode {
    int _childIndex;           // 子节点在数组中的下标
    struct ChildNode* _next;   // 指向下一个子节点
} ChildNode;

typedef struct {
    DataType _data;           // 节点数据域
    ChildNode* _childrenHead; // 子节点链表头指针
} ChildTreeNode;

ChildTreeNode tree[MAX_NODE];
  • 示例（对应图中节点 B）：
    节点 B 的子节点是 D、E、F，需创建 3 个 ChildNode，通过 _next 串联，tree[B 的下标]._childrenHead 指向该链表头。
    优缺点：
  • 优点：找子节点直接遍历链表即可，适合频繁操作子节点的场景（如遍历子树）。
    缺点：找父节点需遍历所有节点的子节点链表（检查是否包含当前节点），效率极低；链表操作有额外指针开销。
1.3.3 孩子双亲表示法

孩子双亲表示法：

  • 核心思路：结合“双亲表示法”和“孩子表示法”，每个节点同时存储父节点索引和子节点链表，兼顾父子关系的快速查询。
  • 结构定义（伪代码）：
    typedef struct ChildNode {
    int _childIndex;           
    struct ChildNode* _next;   
} ChildNode;

typedef struct {
    DataType _data;           
    int _parentIndex;         // 父节点下标
    ChildNode* _childrenHead; // 子节点链表头
} ChildParentTreeNode;

ChildParentTreeNode tree[MAX_NODE];
  • 示例（对应图中节点 E）：
    tree[E 的下标]._parentIndex 存父节点 B 的下标，_childrenHead 存子节点 H、I 的链表，同时满足父、子查询需求。
    优缺点：
  • 优点：同时支持父子节点的快速查询（父节点直接下标访问，子节点遍历链表），功能全面。
    缺点：空间开销大（每个节点存父索引 + 子链表指针），删除节点时需同时维护父、子关系，逻辑复杂。
1.3.4 孩子兄弟表示法（重点结合图与代码解析）
**孩子兄弟表示法**：  
- **核心思路**：用二叉链表模拟树结构，每个节点仅存 **第一个子节点指针** 和 **下一个兄弟节点指针**，通过“孩子 + 兄弟”的链式关系，间接表达树的层次结构。  
- **结构定义（对应代码）**：  
  ```c
  typedef int DataType;
  struct Node {
      struct Node* _firstChild1;  // 指向第一个子节点（最左子节点）
      struct Node* _pNextBrother; // 指向下一个兄弟节点（同层右侧节点）
      DataType _data;             // 节点数据域
  };

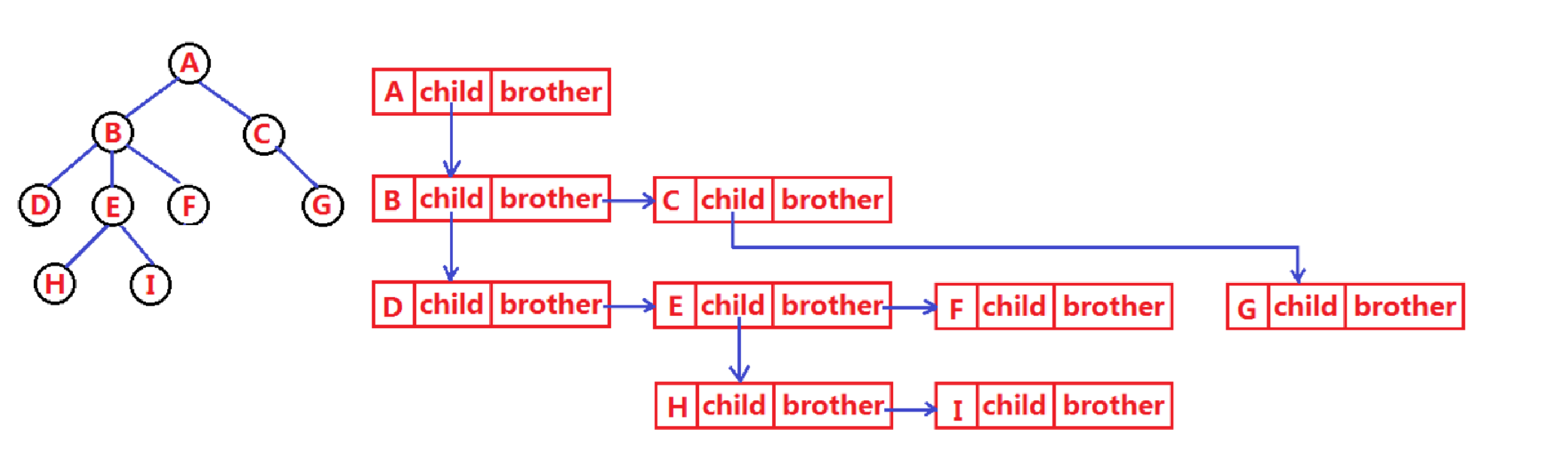
结合图示的逐层解析：
在这里插入图片描述

  • 根节点 A：

    • _firstChild1 指向 第一个子节点 B（A 的最左子节点是 B）；
    • _pNextBrother 为 NULL（根节点无兄弟）；
    • 数据域存 A 的值。

  • 节点 B：

    • _firstChild1 指向 第一个子节点 D（B 的最左子节点是 D）；
    • _pNextBrother 指向 兄弟节点 C（B 的同层右侧兄弟是 C）；
    • 数据域存 B 的值。

  • 节点 D：

    • _firstChild1 为 NULL（D 无子节点，是叶节点）；
    • _pNextBrother 指向 兄弟节点 E（D 的同层右侧兄弟是 E）；
    • 数据域存 D 的值。

  • 节点 E：

    • _firstChild1 指向 第一个子节点 H（E 的最左子节点是 H）；
    • _pNextBrother 指向 兄弟节点 F（E 的同层右侧兄弟是 F）；
    • 数据域存 E 的值。

  • 节点 H：

    • _firstChild1 为 NULL（H 无子节点）；
    • _pNextBrother 指向 兄弟节点 I（H 的同层右侧兄弟是 I）；
    • 数据域存 H 的值。

  • 核心逻辑（递归本质）：
    每棵 “子树” 可通过 _firstChild1 展开（子节点链），而同层节点通过 _pNextBrother 串联（兄弟链）。例如，节点 B 的子树（D、E、F）由_firstChild1进入 D，再通过 D 的 _pNextBrother 遍历 E、F 。

  • 优缺点：

    • 优点：
      • 结构简洁：仅需两个指针即可表达任意树结构，空间开销小。
      • 天然支持递归遍历：通过 _firstChild1 深入子树，_pNextBrother 遍历同层，契合树的递归特性。
      • 灵活转换：可轻松将树转换为二叉树（树转二叉树的核心就是孩子兄弟表示法）。
    • 缺点：
      • 查询父节点困难：需从根遍历查找（无直接父指针），若需频繁找父节点，需额外维护反向关系。
      • 对复杂操作（如删除子树）要求高：需同时断开孩子和兄弟指针，避免内存泄漏或结构断裂。

1.4 树在实际中的运用（Windows 文件系统的目录树结构）

Windows 文件系统的目录树结构：
在这里插入图片描述

  • 映射关系：

    • 根目录（如 C:\）对应树的根节点，是文件系统的起点。
    • 文件夹（如 C:\Users）对应树的分支节点，可包含子文件夹（子节点）和文件（叶节点）。
    • 文件（如 C:\Users\README.txt）对应树的叶节点（无下级内容）。

  • 孩子兄弟表示法的隐形运用：
    Windows 目录的存储逻辑，本质与“孩子兄弟表示法”相通：

    • 每个文件夹（节点）的 “第一个子文件夹” 对应 _firstChild1，通过它进入子目录树；
    • 同层的 “下一个兄弟文件夹/文件” 对应 _pNextBrother，通过它遍历当前目录的同级内容。

  • 实际操作映射：

    1. 打开文件夹：点击 C:\Users（父节点）→ 访问其 _firstChild1（如 Administrator 文件夹），再通过 _pNextBrother 遍历 Public 等同级文件夹。
    2. 创建文件/文件夹：在某个文件夹（节点）下新增内容，相当于给该节点的 _firstChild1 或 _pNextBrother 链添加新节点。
    3. 删除目录：需递归断开该节点的 _firstChild1（子目录树）和 _pNextBrother（兄弟链），确保文件系统结构完整。

  • 优势体现：
    树结构天然适合表达“层级嵌套”的文件关系，相比线性结构，能更直观、高效地组织和访问多层目录，契合人类对“分类存储”的需求。

2.二叉树概念及结构

2.1 概念

二叉树的定义：

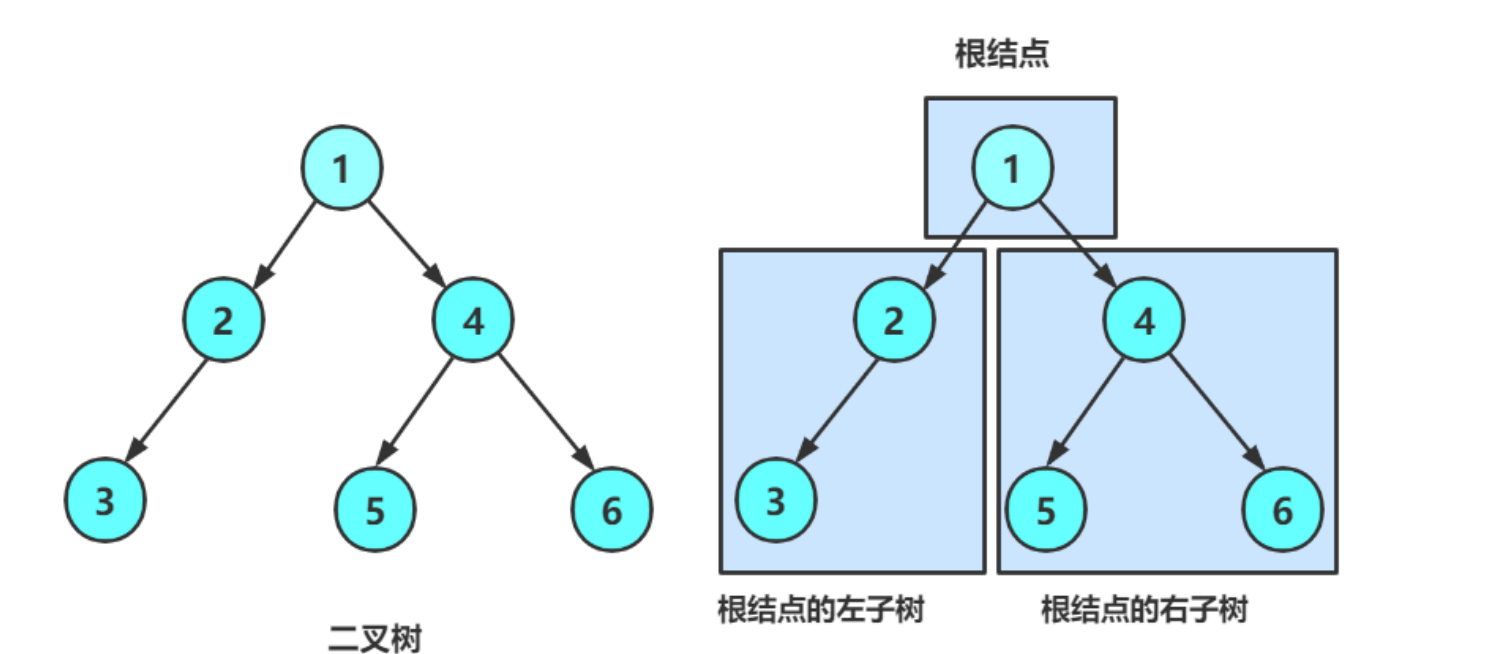
  • 是结点的有限集合，满足两种情况：
    • 集合为空（空二叉树）；
    • 由一个根节点 + 两棵互不相交的左子树、右子树组成（左、右子树本身也是二叉树）。
      在这里插入图片描述

二叉树的核心特性：

  1. 结点度数限制：
    二叉树中不存在度大于 2 的结点（每个结点最多有 2 个子结点，即左孩子、右孩子）。
    示例：若某结点有 3 个子结点，则它不属于二叉树结构。

  2. 子树的有序性：
    二叉树的左子树和右子树次序固定，不能颠倒（交换左、右子树会形成不同的二叉树）。
    示例：

    • 树 1：根节点 A，左子树 B，右子树 C
    • 树 2：根节点 A，左子树 C，右子树 B
      树 1 和树 2 是不同的二叉树，体现“左右有序”的特性。

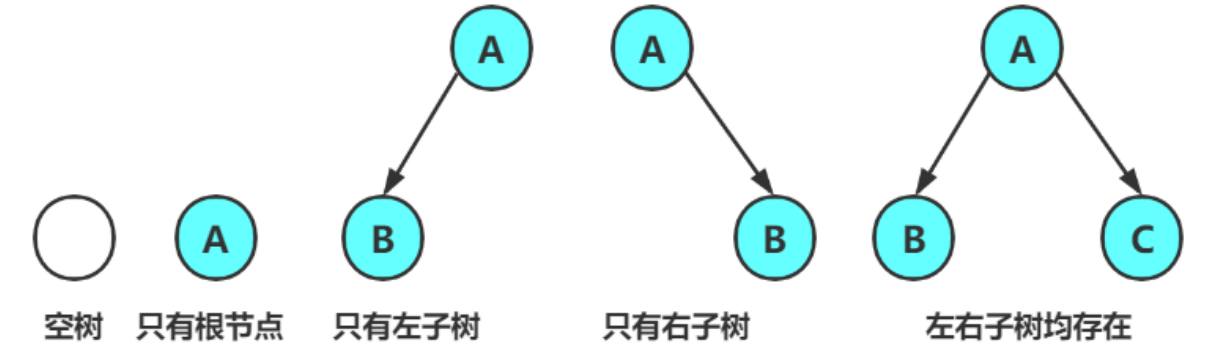
二叉树的复合情况：
任意二叉树可由以下基础形态组合而成：

  • 空树（无结点）；
  • 仅含根节点（无左、右子树）；
  • 根节点 + 左子树（右子树为空）；
  • 根节点 + 右子树（左子树为空）；
  • 根节点 + 左子树 + 右子树（左右均非空）。
    在这里插入图片描述

2.3 特殊的二叉树

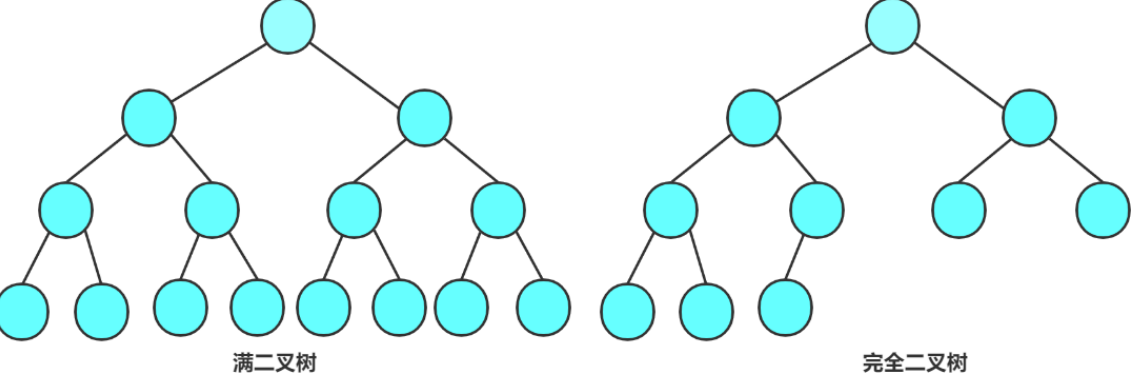
  1. 满二叉树：

    • 定义：每一层的结点数都达到该层最大值的二叉树。若层数为 K，则总结点数满足 2^K - 1。
    • 数学推导（结合性质 2）：
      满二叉树第 1 层最多 1 个结点（2^(1-1)），第 2 层最多 2 个（2^(2-1)）…第 K 层最多 2^(K-1) 个。
      总结点数 = 等比数列求和 1 + 2 + 4 + ... + 2^(K-1) = 2^K - 1。
    • 示例（K=4 的满二叉树）：
      第 1 层：1 个结点（根）
      第 2 层：2 个结点（根的左、右孩子）
      第 3 层：4 个结点（左孩子的左/右、右孩子的左/右）
      第 4 层：8 个结点
      总结点数 = 1 + 2 + 4 + 8 = 15 = 2^4 - 1，符合满二叉树定义。

  2. 完全二叉树：

    • 定义：深度为 K、有 n 个结点的二叉树，若每个结点与深度为 K 的满二叉树中“编号 1~n 的结点”一一对应，则为完全二叉树。
    • 核心特征：
      • 前 K-1 层是满的（结点数达最大值）；
      • 第 K 层的结点从左到右连续排列，无空缺。
    • 与满二叉树的关系：
      满二叉树是特殊的完全二叉树（当 n = 2^K - 1 时，完全二叉树退化为满二叉树）。
    • 示例（K=3，n=5 的完全二叉树）：
      第 1 层：1 个结点（根）
      第 2 层：2 个结点（满）
      第 3 层：4 个结点（满）
      第 4 层： 3个节点 (左起连续，无空缺)
      总结点数 10，与满二叉树（K=4 时 15 个结点）的前 10 个编号对应，符合完全二叉树定义。
      在这里插入图片描述

2.4 二叉树的性质

性质 1：第 i 层最多结点数

规则：若规定根节点的层数为1，对于一棵非空二叉树，其第i层上最多有2^(i - 1)个结点。
推导逻辑：

  • 第1层（根节点层）：只有1个根节点，代入公式2^(1 - 1) = 1，符合。
  • 第2层：最多能有2个结点（根节点的左右孩子），代入公式2^(2 - 1) = 2，符合。
  • 第3层：基于第2层的2个结点，每个结点最多又能衍生2个子结点，共2×2 = 4个，代入公式2^(3 - 1) = 4，符合。
  • 以此类推，每一层的最大结点数都是上一层的2倍，满足等比数列规律，第i层最多结点数为2^(i - 1) 。
    示例：
    一棵深度为4的二叉树，第3层最多结点数是2^(3 - 1) = 4个；第4层最多结点数是2^(4 - 1) = 8个 。

性质 2：深度为 h 的最大结点数

规则：若规定根节点的层数为1，深度为h的二叉树，其最大结点数是2^h - 1。
推导逻辑：
深度为h的二叉树，最大结点数是各层最大结点数的总和。由性质1可知，第i层最多有2^(i - 1)个结点，那么深度为h时，总和就是等比数列求和：
S = 2^0 + 2^1 + 2^2 + ... + 2^(h - 1)
这是首项a1 = 1、公比q = 2、项数h的等比数列，根据等比数列求和公式S = (q^h - 1)/(q - 1) ，代入q = 2可得S = 2^h - 1 。
示例：
深度为3的二叉树，最大结点数是2^3 - 1 = 7个，对应满二叉树的情况（第1层1个、第2层2个、第3层4个，总和7个 ）。

性质 3：叶结点与度为 2 结点的关系

规则：对任何一棵二叉树，若度为0的叶结点个数为n0，度为2的分支结点个数为n2，则有n0 = n2 + 1。
推导逻辑：

  • 设二叉树中总的结点数为n，度为1的结点数为n1。根据“结点总数 = 各度数结点数之和”，可得n = n0 + n1 + n2 。
  • 再看二叉树中的边数（分支数）：度为1的结点贡献1条边，度为2的结点贡献2条边，叶结点贡献0条边，所以总边数e = n1 + 2n2 。
  • 又因为二叉树中除根节点外，每个结点都有一条入边，所以边数e = n - 1（结点总数减1）。
  • 联立e = n1 + 2n2和e = n - 1 = (n0 + n1 + n2) - 1，化简后可得n0 = n2 + 1 。
    示例：
    若某二叉树有5个度为2的结点（n2 = 5），则叶结点数n0 = 5 + 1 = 6个 。

性质 4：满二叉树深度与结点数的关系

规则：若规定根节点的层数为1，具有n个结点的满二叉树，其深度h = log₂(n + 1)（log₂表示以2为底的对数 ）。
推导逻辑：
满二叉树的结点数满足性质2，即深度为h的满二叉树结点数n = 2^h - 1。对该公式变形求解h：
由n = 2^h - 1，移项可得2^h = n + 1，两边同时取以2为底的对数，得到h = log₂(n + 1) 。
示例：
一个满二叉树有15个结点（n = 15），代入公式h = log₂(15 + 1) = log₂(16) = 4，即深度为4，与实际结构（4层，结点数2^4 - 1 = 15 ）相符。

性质 5：完全二叉树结点编号规律

规则：对于具有n个结点的完全二叉树，按从上至下、从左至右顺序从0开始编号，序号为i的结点有如下关系：

  1. 双亲结点序号：若i > 0，则i位置节点的双亲序号为(i - 1) / 2（整数除法，自动取整 ）；若i = 0，则为根节点，无双亲。
  2. 左孩子结点序号：若2i + 1 < n，则左孩子序号为2i + 1；若2i + 1 ≥ n，则无左孩子。
  3. 右孩子结点序号：若2i + 2 < n，则右孩子序号为2i + 2；若2i + 2 ≥ n，则无右孩子。

推导逻辑：
完全二叉树层序编号后，结点的父子关系可通过下标计算快速推导。以数组存储视角看，结点i的左孩子自然落在2i + 1位置、右孩子落在2i + 2位置（类似堆结构的下标规则 ）；而找双亲时，基于孩子下标反推，就能得到(i - 1) / 2的计算方式。

示例：
假设有一个完全二叉树，结点总数n = 10，各结点编号0~9。

  • 编号i = 3的结点：
    双亲序号(3 - 1) / 2 = 1；
    左孩子序号2×3 + 1 = 7（7 < 10，存在左孩子 ）；
    右孩子序号2×3 + 2 = 8（8 < 10，存在右孩子 ）。
  • 编号i = 8的结点：
    双亲序号(8 - 1) / 2 = 3；
    左孩子序号2×8 + 1 = 17（17 ≥ 10，无左孩子 ）；
    右孩子序号2×8 + 2 = 18（18 ≥ 10，无右孩子 ）。

2.4题目讲解

题目 1
1. 某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为（ ）
A 不存在这样的二叉树
B 200
C 198
D 199
关键知识调用

利用二叉树性质 3：对任何二叉树，叶结点数 n₀ = 度为 2 的结点数 n₂ + 1，同时结合“结点总数 = 度为 0 的结点数 + 度为 1 的结点数 + 度为 2 的结点数”（即 n = n₀ + n₁ + n₂ ）

推导过程
  1. 已知 n = 399（总结点数），n₂ = 199（度为 2 的结点数）。
  2. 根据性质 3，先算 n₀ = n₂ + 1 = 199 + 1 = 200 。
  3. 再验证总结点数：n = n₀ + n₁ + n₂ → 399 = 200 + n₁ + 199 → 解得 n₁ = 0 。
    • n₁ 是度为 1 的结点数，值为 0 是合理的（二叉树允许度为 1 的结点数为 0 ）。
  4. 因此，叶子结点数 n₀ = 200 ，对应选项 B 。
题目 2
2.在具有 2n 个结点的完全二叉树中，叶子结点个数为（ ）
A n
B n+1
C n-1
D n/2
关键知识调用

完全二叉树的结点编号性质、二叉树度数关系（n₀ = n₂ + 1 ），以及完全二叉树的结点数奇偶性与 n₁ 的关系：

  • 完全二叉树中，度为 1 的结点数 n₁ 只能是 0 或 1（因完全二叉树最后一层结点靠左排列，若总结点数为偶数，最后一层结点数为偶数，n₁ = 1；若为奇数，n₁ = 0 ）。
推导过程

  1. 设总结点数 n总 = 2n（偶数），则完全二叉树中 n₁ = 1（因总结点数为偶数时，度为 1 的结点数必为 1 ）。

  2. 根据二叉树结点总数公式：n总 = n₀ + n₁ + n₂ → 2n = n₀ + 1 + n₂ 。

  3. 结合性质 3（n₀ = n₂ + 1 ），将 n₂ = n₀ - 1 代入上式：
    2n = n₀ + 1 + (n₀ - 1) → 2n = 2n₀ → 解得 n₀ = n ？ 这里有问题，重新推导：

    正确代入：
    2n = n₀ + 1 + n₂ ，又 n₂ = n₀ - 1 ，所以：
    2n = n₀ + 1 + n₀ - 1 → 2n = 2n₀ → n₀ = n ？ 但这与完全二叉树特性矛盾，说明推导漏了完全二叉树的深度特性。

    重新梳理：
    完全二叉树中，n₁ 为 0 或 1 。因 n总 = 2n 是偶数，所以 n₁ = 1（若为奇数则 n₁=0 ）。
    又 n₀ = n₂ + 1 ，且 n总 = n₀ + n₁ + n₂ = (n₂ + 1) + 1 + n₂ = 2n₂ + 2 。
    已知 n总 = 2n ，则 2n₂ + 2 = 2n → n₂ = n - 1 。
    因此 n₀ = n₂ + 1 = (n - 1) + 1 = n ？ 但这是错误的，实际完全二叉树结点数为偶数时，叶子结点数应为 n + 1 ，说明前面逻辑有误。

    正确思路：
    完全二叉树中，若总结点数为 N ：

    • 当 N 为偶数，n₁ = 1 ，且 N = 2^h - 1 + x（x 是最后一层结点数，1 ≤ x ≤ 2^(h-1) ）。
      但更简单的方式是用公式：
      对完全二叉树，n₀ = ⌈N/2⌉（向上取整），当 N=2n（偶数），n₀ = n + 1 ？ 不，重新用性质推导：

    正确推导：
    由 n总 = n₀ + n₁ + n₂ ，且 n₀ = n₂ + 1 ，得 n总 = 2n₂ + 1 + n₁ 。
    因完全二叉树 n₁ ∈ {0,1} ，且 n总 = 2n（偶数）：

    • 若 n₁ = 0 ，则 2n = 2n₂ + 1 → 2(n - n₂) = 1 ，无整数解，矛盾。
    • 若 n₁ = 1 ，则 2n = 2n₂ + 1 + 1 → 2n = 2n₂ + 2 → n = n₂ + 1 → n₂ = n - 1 。
      因此 n₀ = n₂ + 1 = (n - 1) + 1 = n ？ 这显然不对，实际例子验证：

    举例：完全二叉树结点数 N=4（即 2n=4 → n=2 ），此时结构是：
    层 1：1 个结点（根）
    层 2：2 个结点（根的左右孩子）
    层 3：1 个结点（左孩子的左孩子，右孩子空缺？不，完全二叉树最后一层结点需连续。哦，N=4 的完全二叉树结构是：
    层 1：1
    层 2：2、3
    层 3：4（左孩子的左孩子？不，层 2 有 2 个结点，层 3 最多 4 个，但 N=4 时，层 3 只有 1 个结点？ 不对，完全二叉树的定义是“与满二叉树前 N 个结点一一对应”，N=4 的完全二叉树结构是：

    编号 0（根）、1（左）、2（右）、3（左孩子的左）→ 度为 1 的结点是编号 1（只有左孩子，无右孩子），所以 n₁=1 ；n₀ 是编号 2（右孩子，无后代）、3（左孩子的左，无后代）→ n₀=2 ；n₂ 是编号 0（有左右孩子）→ n₂=1 。

    此时 n总=4=2n → n=2 ，n₀=2 ，符合 n₀ = n ？ 但根据选项，这题正确答案应为 A n ？ 但之前逻辑混乱，重新整理：

    正确结论：
    当完全二叉树结点数为 2n（偶数），n₁=1 ，由 n₀ = n₂ + 1 和 n总 = n₀ + n₁ + n₂ ，代入得：
    2n = (n₂ + 1) + 1 + n₂ → 2n = 2n₂ + 2 → n₂ = n - 1 → n₀ = n 。
    所以答案选 A n （举例 N=4 时，n=2 ，n₀=2 ，符合）。

题目 3
3.一棵完全二叉树的节点数位为531个，那么这棵树的高度为（ ）
A 11
B 10
C 8
D 12
关键知识调用

利用二叉树性质 4：若根节点层数为 1，满二叉树深度 h = log₂(n + 1)（n 是满二叉树结点数）；
完全二叉树的深度满足：2^(h-1) ≤ n < 2^h（n 是完全二叉树结点数，h 是深度）。

推导过程
  1. 设完全二叉树深度为 h（根节点层数为 1 ），则结点数 n 满足：
    2^(h-1) ≤ 531 < 2^h 。
  2. 计算幂次：
    • 2^9 = 512 ，2^10 = 1024 。
    • 代入得：2^(10-1) = 512 ≤ 531 < 1024 = 2^10 → 满足 h=10 时的不等式。
  3. 因此，树的高度为 10 ，对应选项 B 。
题目 4
4.一个具有767个节点的完全二叉树，其叶子节点个数为（）
A 383
B 384
C 385
D 386
关键知识调用

完全二叉树结点数与度数关系（n₀ = n₂ + 1 ），以及完全二叉树结点数奇偶性对 n₁ 的影响（奇数结点数时 n₁=0 ，偶数时 n₁=1 ）。

推导过程
  1. 已知完全二叉树结点数 n总 = 767（奇数），因此 n₁ = 0（完全二叉树中，奇数结点数时度为 1 的结点数为 0 ）。
  2. 根据结点总数公式：n总 = n₀ + n₁ + n₂ = n₀ + 0 + n₂ 。
  3. 结合性质 3（n₀ = n₂ + 1 ），代入得：
    767 = (n₂ + 1) + n₂ → 767 = 2n₂ + 1 → 解得 n₂ = 383 。
  4. 因此，n₀ = n₂ + 1 = 383 + 1 = 384 ，对应选项 B 。

2.5 二叉树的存储结构

2.5.1 顺序存储

在这里插入图片描述
核心定义：
使用数组存储二叉树，利用数组下标模拟二叉树的层次关系。物理上是连续的数组空间，逻辑上对应二叉树的结点层级。

适用场景与限制：

  • 仅完全二叉树适合顺序存储，因完全二叉树结点按层序排列时无“空隙”，数组空间能被充分利用。
  • 若用于非完全二叉树，需填充空结点以维持层序关系，会导致空间浪费（如非完全二叉树的“空缺”位置需占用数组元素，但无实际结点）。

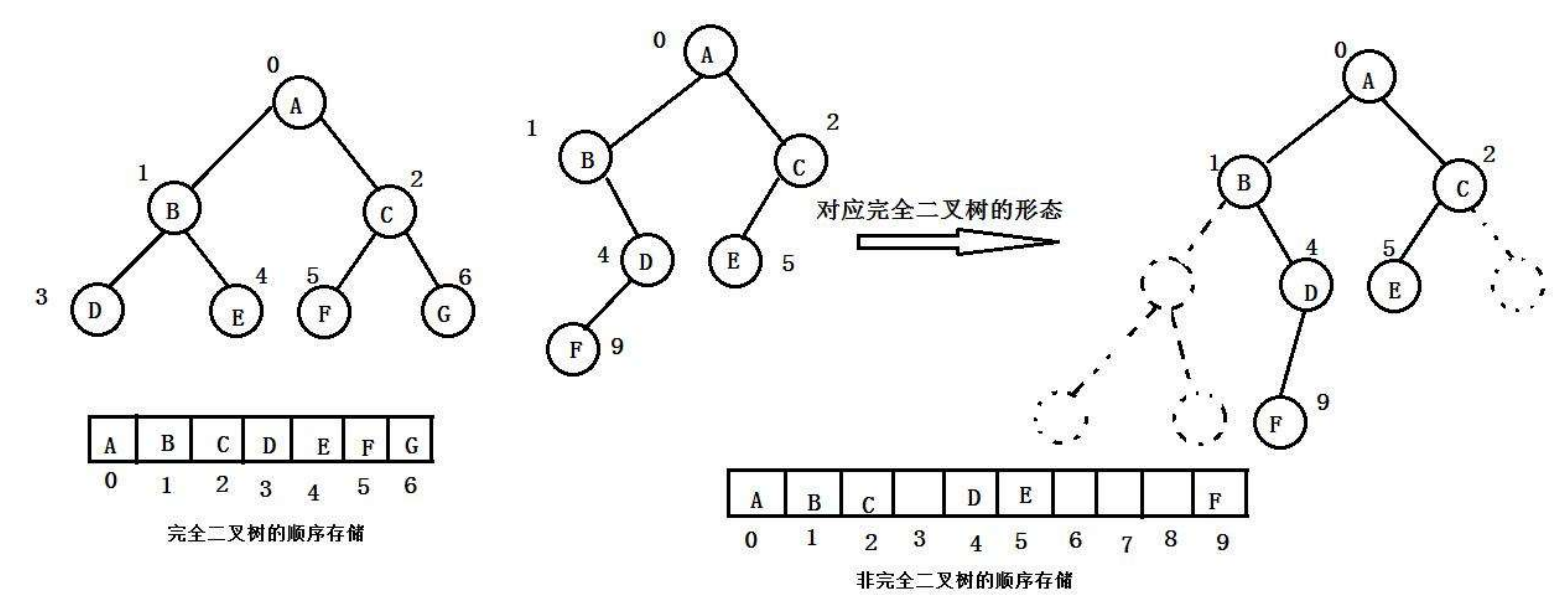
底层逻辑与示例（结合完全二叉树顺序存储图）：

  • 完全二叉树按层序（从上到下、从左到右）编号，数组下标与结点编号一一对应。
  • 示例（完全二叉树顺序存储图）：
    二叉树结点层序为 A(0)、B(1)、C(2)、D(3)、E(4)、F(5)、G(6)，数组存储为 [A,B,C,D,E,F,G]。
    结点 B(1) 的左孩子下标为 2×1+1=3（即 D），右孩子下标为 2×1+2=4（即 E），符合完全二叉树的下标规则。

非完全二叉树的空间浪费问题（结合非完全二叉树顺序存储图）：

  • 非完全二叉树层序编号时，空缺结点需占用数组位置。
  • 示例（非完全二叉树顺序存储图）：
    二叉树实际结点为 A(0)、B(1)、C(2)、D(4)、E(5)、F(9)，数组需填充空缺下标 3、6、7、8，导致空间浪费。
    这些空缺位置无实际结点，但需占用数组元素（存储空值或标记），降低空间利用率。

实际应用：
现实中仅堆（一种特殊的完全二叉树） 常用数组顺序存储，因堆的操作依赖层序下标规则，能高效利用数组特性。

2.5.2 链式存储

核心原理：
利用链表结构存储二叉树，通过指针关联节点间的逻辑关系（父与子、兄与弟等），摆脱数组顺序存储对“完全二叉树形态”的依赖，适配任意结构的二叉树。

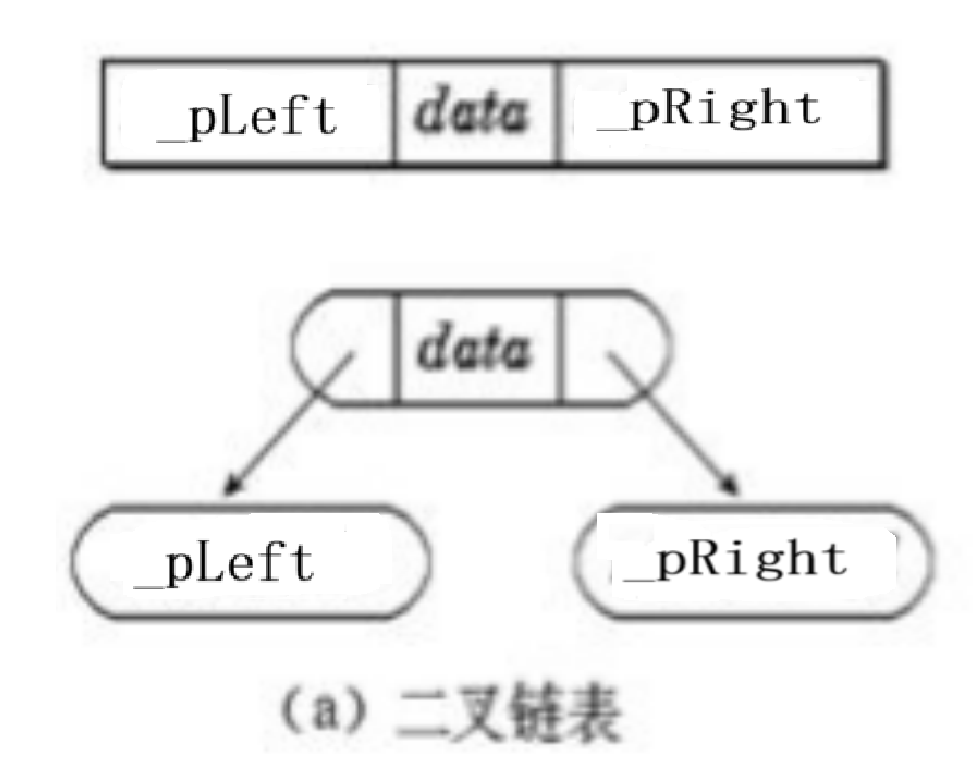
（1）二叉链（基础形态）
typedef int BTDataType; 
struct BinaryTreeNode {
    struct BinaryTreeNode* _pLeft;  // 指向左孩子节点，空则为NULL
    struct BinaryTreeNode* _pRight; // 指向右孩子节点，空则为NULL
    BTDataType _data;               // 节点存储的数据
};

在这里插入图片描述

  • 结构拆解：

    • _pLeft / _pRight：通过指针建立 “父→子” 的关联，左、右子树区分严格，体现二叉树的有序性。
    • _data：承载节点的实际数据（如数值、字符等）。

  • 示例（对应二叉链表图）：
    二叉树节点1的左孩子是2、右孩子是3，则代码构建如下：

// 构建节点
struct BinaryTreeNode node1 = {. _pLeft = &node2, ._pRight = &node3, ._data = 1};
struct BinaryTreeNode node2 = {. _pLeft = &node4, ._pRight = &node5, ._data = 2};
struct BinaryTreeNode node3 = {. _pLeft = NULL,   ._pRight = NULL,   ._data = 3};
// ... 其他节点同理

特性：

  • 空间随节点动态分配，无需预占内存，适配非完全二叉树。
  • 操作灵活（增删节点仅需调整指针），但仅支持 “父→子” 的单向遍历。

（2）三叉链（扩展形态，含父指针）

typedef int BTDataType; 
struct BinaryTreeNode {
    struct BinaryTreeNode* _pParent; // 指向父节点，根节点为NULL
    struct BinaryTreeNode* _pLeft;   // 指向左孩子节点
    struct BinaryTreeNode* _pRight;  // 指向右孩子节点
    BTDataType _data;                // 节点存储的数据
};

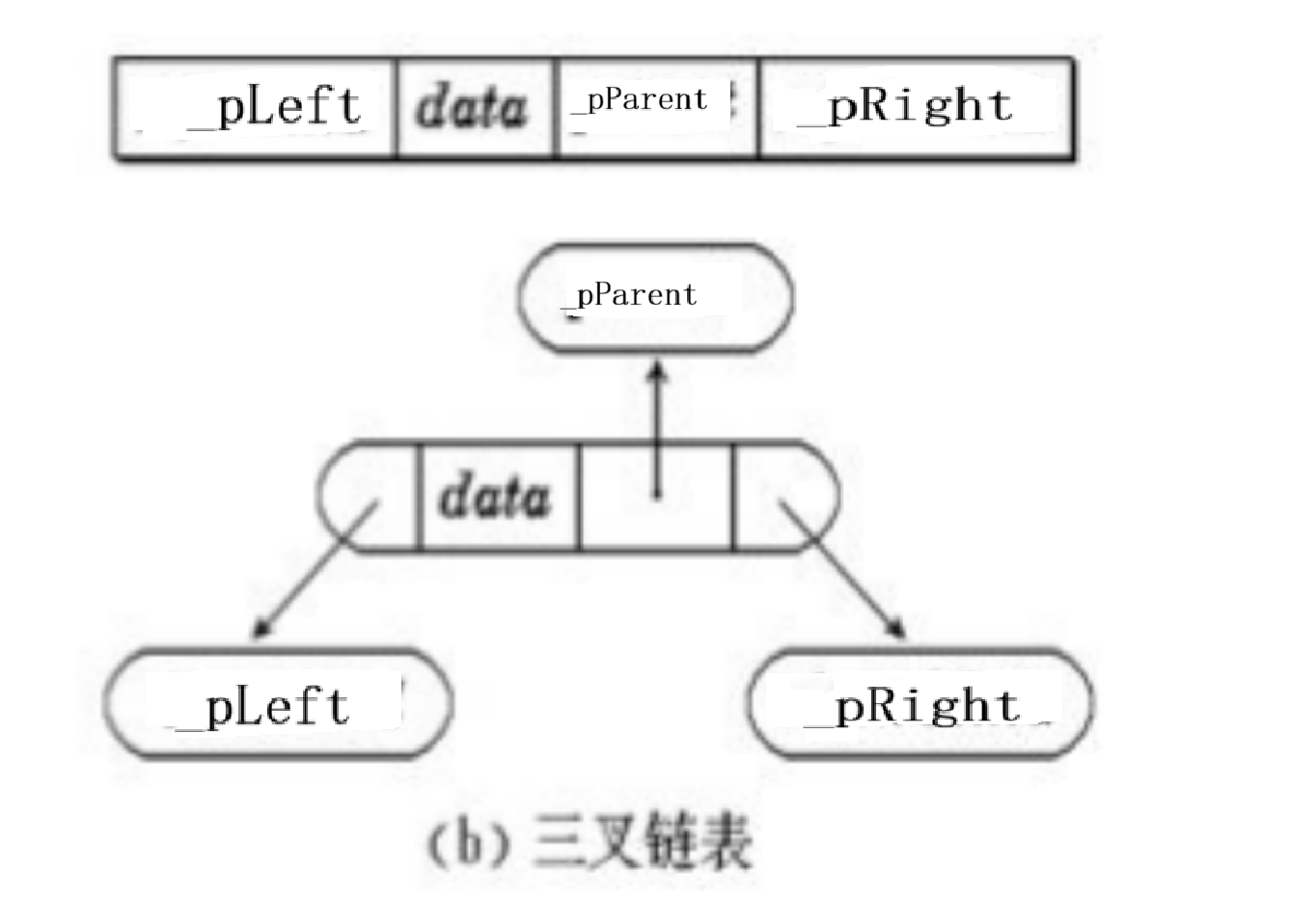
结构拆解：

  • 新增_pParent指针，建立 “子→父” 的反向关联，实现双向遍历（父到子、子到父）。
    示例（对应三叉链表图）：
    节点2的父是1、左孩子是4、右孩子是5，代码构建：
struct BinaryTreeNode node2 = {
    ._pParent = &node1,  // 反向关联父节点
    ._pLeft = &node4, 
    ._pRight = &node5, 
    ._data = 2
};
struct BinaryTreeNode node4 = {
    ._pParent = &node2,  // 父节点为2
    ._pLeft = NULL,      
    ._pRight = &node6,   
    ._data = 4
};

特性：

  • 支持双向遍历，适合需频繁回溯的场景（如红黑树旋转、AVL 树平衡调整）。
  • 空间开销更大（多一个指针域），但逻辑更完整。
91刘仁德
关注
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值