【动态规划】子数组问题

一、经验总结

对于动态规划中的子数组问题，在状态分析过程中，除了一般经验外（以i位置为起点或终点），还要继续进行细分。

以i位置为终点的子数组包括：

1. 长度为1：i位置的元素自成一个单元素子数组
2. 长度大于1：以i位置结尾的多元素子数组

在完成初步的状态表示后，进行更为细致的分析，同时推导状态转移方程。如果发现之前设定的状态不够用（需要更多的dp表），则设置所需要的其他状态。

通过以下方法将推导思路化简整理为简单的代码逻辑：

• 相同结果进行合并；
• 设置dp表元素的初始值；
• 取最大最小值；

动态规划dp表的初始化方案：

1. 将位于dp表端点（边界）的位置初始化。
2. 创建虚拟节点并赋值，注意：1.虚拟节点的初始值，保证后续填表正确 2.dp表与原数组的下标映射关系
3. 将dp表的所有元素初始化为该状态的下限。

---

二、相关编程题

2.1 最大子数组和

题目链接

53. 最大子数组和 - 力扣（LeetCode）

题目描述

算法原理

编写代码

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int n = nums.size();
        vector<int> dp(n);
        dp[0] = nums[0];
        int ret = dp[0];
        for(int i = 1; i < n; ++i)
        {
            dp[i] = max(nums[i], dp[i-1]+nums[i]);
            ret = max(ret, dp[i]);
        }
        return ret;
    }
};

---

2.2 环形子数组的最大和

题目链接

918. 环形子数组的最大和 - 力扣（LeetCode）

题目描述

算法原理

编写代码

class Solution {
public:
    int maxSubarraySumCircular(vector<int>& nums) {
        int n = nums.size();
        vector<int> f(n), g(n);
        f[0] = g[0] = nums[0];
        int f_max=f[0], g_min=g[0];
        for(int i = 1; i < n; ++i)
        {
            f[i] = max(nums[i], f[i-1]+nums[i]);
            g[i] = min(nums[i], g[i-1]+nums[i]);
            f_max = max(f_max, f[i]);
            g_min = min(g_min, g[i]);
        }
        int sum = 0;
        for(auto e : nums) sum += e;
        if(g_min == sum) return f_max;
        else return max(f_max, sum-g_min);
    }
};

---

2.3 乘积最大子数组

题目链接

152. 乘积最大子数组 - 力扣（LeetCode）

题目描述

算法原理

编写代码

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int n = nums.size();
        vector<double> f(n), g(n);
        f[0] = g[0] = nums[0];
        double ret = f[0];
        for (int i = 1; i < n; ++i) {
            f[i] = max((double)nums[i], max(f[i - 1] * nums[i], g[i - 1] * nums[i]));
            g[i] = min((double)nums[i], min(f[i - 1] * nums[i], g[i - 1] * nums[i]));
            ret = max(ret, f[i]);
        }
        return ret;
    }
};

---

2.4 乘积为正数的最长子数组

题目链接

1567. 乘积为正数的最长子数组长度 - 力扣（LeetCode）

题目描述

算法原理

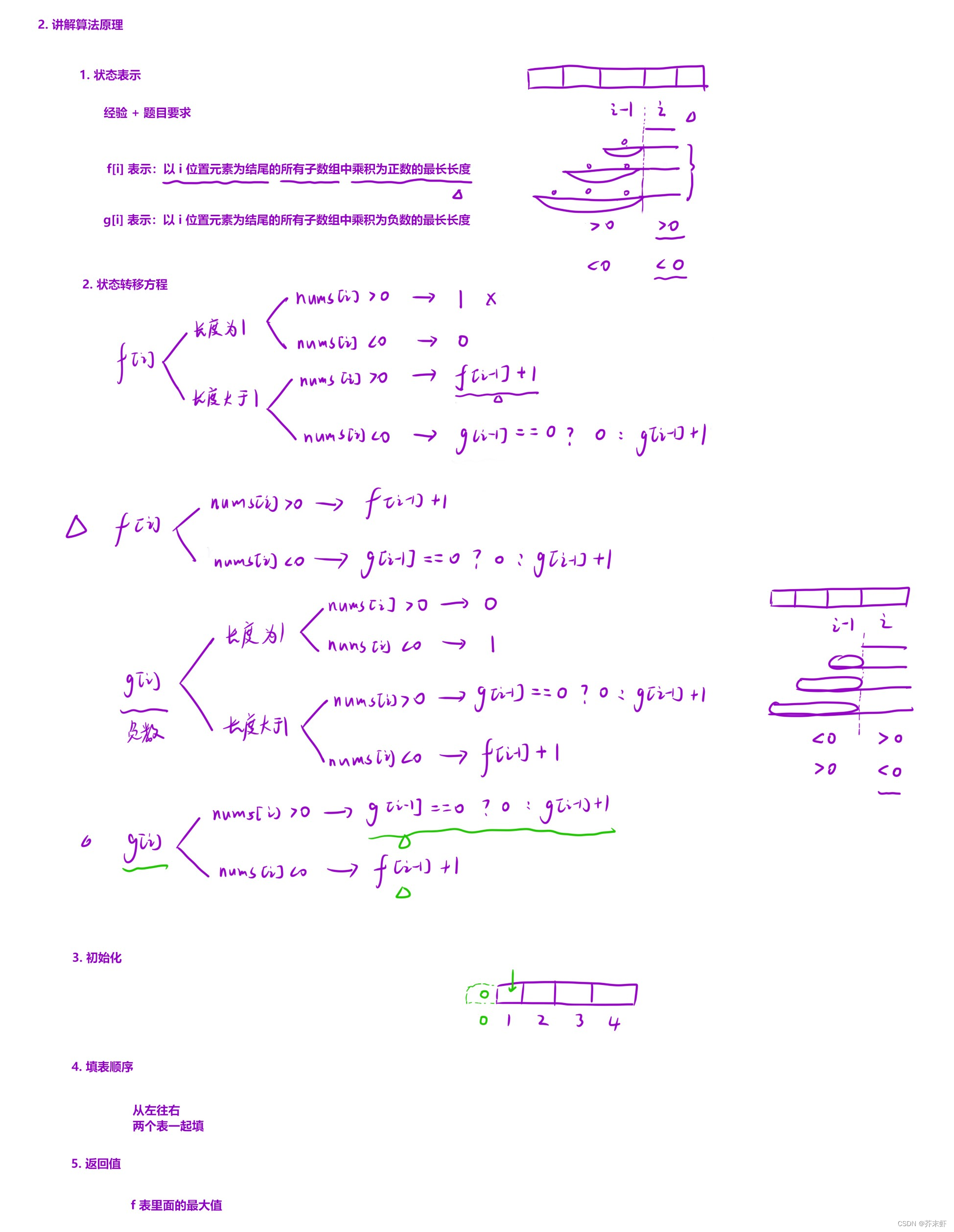
编写代码

class Solution {
public:
    int getMaxLen(vector<int>& nums) {
        int n = nums.size();
        vector<int> f(n+1), g(n+1);
        int ret = 0;
        for(int i = 1; i <= n; ++i)
        {
            if(nums[i-1] > 0)
            {
                f[i] = f[i-1]+1;
                g[i] = g[i-1]==0? 0:g[i-1]+1;
            }
            else if(nums[i-1] < 0)
            {
                f[i] = g[i-1]==0? 0:g[i-1]+1;
                g[i] = f[i-1]+1;
            } 
            ret = max(ret, f[i]);
        }
        return ret;
    }
};

---

2.5 等差数列划分

题目链接

413. 等差数列划分 - 力扣（LeetCode）

题目描述

算法原理

编写代码

class Solution {
public:
    int numberOfArithmeticSlices(vector<int>& nums) {
        int n = nums.size();
        if(n<3) return 0;
        vector<int> dp(n);
        dp[0] = dp[1] = 0;
        int ret = 0;
        for(int i = 2; i < n; ++i)
        {
            if(nums[i]-nums[i-1] == nums[i-1]-nums[i-2])
            {
                dp[i] = dp[i-1]+1;
            }
            ret += dp[i];
        }
        return ret;
    }
};

---

2.6 最长湍流子数组

题目链接

978. 最长湍流子数组 - 力扣（LeetCode）

题目描述

算法原理

编写代码

//解法一：双dp表
class Solution {
public:
    int maxTurbulenceSize(vector<int>& arr) {
        int n = arr.size();
        vector<int> f(n, 1), g(n, 1);
        int ret = 1;
        for (int i = 1; i < n; i++) {
            if (arr[i - 1] < arr[i])
                f[i] = g[i - 1] + 1;
            else if (arr[i - 1] > arr[i])
                g[i] = f[i - 1] + 1;
            ret = max(ret, max(f[i], g[i]));
        }
        return ret;
    }
};

//解法二：单dp表
class Solution {
public:
    int maxTurbulenceSize(vector<int>& arr) {
        int n = arr.size();
        if(n == 1) return 1;
        vector<int> dp(n, 1);
        dp[0] = 1;
        dp[1] = arr[0]==arr[1]? 1:2;
        int ret = dp[1];
        for(int i = 2; i < n; ++i)
        {
            if(arr[i]==arr[i-1])
                dp[i] = 1;
            else if((double)(arr[i-1]-arr[i-2])/(arr[i]-arr[i-1])<0) //乘法变除法，防止越界
                dp[i] = dp[i-1]+1;
            else
                dp[i] = 2;
            ret = max(ret, dp[i]);         
        }
        return ret;
    }
};
//乘法变除法，防止越界，需要注意：
//1.避免除0错误
//2.需要强转成double保留小数

---

2.7 单词拆分

题目链接

139. 单词拆分 - 力扣（LeetCode）

题目描述

算法原理

编写代码

class Solution {
public:
    bool wordBreak(string s, vector<string>& Dict) {
        unordered_set<string> hash;
        for(string& str:Dict) hash.insert(str);
        int n = s.size();
        s = " "+s;
        vector<bool> dp(n+1);
        dp[0] = true;
        for(int i = 1; i <= n; ++i)
        {
            for(int j = 1; j <= i; ++j)
            {
                if(dp[j-1] && hash.count(s.substr(j, i-j+1)))
                {
                    dp[i] = true;
                    break;
                } 
            }
        }
        return dp[n];
    }
};

---

2.8 环绕字符串中唯一的子字符串

题目链接

467. 环绕字符串中唯一的子字符串 - 力扣（LeetCode）

题目描述

算法原理

编写代码

class Solution {
public:
    int findSubstringInWraproundString(string s) {
        int n = s.size();
        vector<int> dp(n, 1);
        for(int i = 1; i < n; ++i)
        {
            if(s[i-1]+1==s[i] || s[i-1]=='z'&&s[i]=='a')
                dp[i] += dp[i-1];
        }
        int hash[26] = {0};
        for(int i = 0; i < n; ++i)
        {
            int chi = s[i]-'a';
            hash[chi] = max(hash[chi], dp[i]);
        }
        int ret = 0;
        for(auto e : hash) ret+=e;
        return ret;
    }
};