实验目的:
1 掌握正态分布下的最小错误贝叶斯分类器的设计
2 掌握正态分布下的最小风险贝叶斯分类器的设计
实验环境
Python
实验数据:
假定某个区域细胞识别中正常细胞(w1)和异常细胞(w2)两类的先验概率分别是:
P(w1)=0.9, P(w2)=0.1。
现有一系列呆观察的细胞,其观察值为x:
-3.9847 -3.5549 -1.2401 -0.9780 -0.7932 -2.8531 -2.7605 -3.7287 – 3.5414 -2.2692
-3.4549 -3.0752 -3.9934 2.8792 -0.9780 0.7932 1.1882 3.0682 -1.5799 -1.4885 -0.7431
-0.4221 -1.1186 4.2532
已知类条件概率分布服从正态分布:
P(x|w1)服从的正太分布为(-2, 0.25)
P(x|w2)服从的正太分布为(2, 4)
实验要求:
1请根据上述数据设计程序,画出相应的分布曲线和分类结果,并比较。
2 若最小风险贝叶斯决策表如下表
|
决策 状态 |
w1 |
w2 |
|
a1 |
0 |
6 |
|
a2 |
1 |
0 |
所示:
请根据上述数据设计程序,画出相应的分布曲线和分类结果,并比较。
以下是我的代码部分
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 给定的数据和参数
data = [-3.9847, -3.5549, -1.2401, -0.9780, -0.7932, -2.8531, -2.7605, -3.7287, 3.5414, -2.2692,
-3.4549, -3.0752, -3.9934, 2.8792, -0.9780, 0.7932, 1.1882, 3.0682, -1.5799, -1.4885, -0.7431,
-0.4221, -1.1186, 4.2532]
prior_w1 = 0.9
prior_w2 = 0.1
# 类条件概率分布的参数
mean_w1 = -2
variance_w1 = 0.25
std_dev_w1 = np.sqrt(variance_w1)
mean_w2 = 2
variance_w2 = 4
std_dev_w2 = np.sqrt(variance_w2)
# 定义正态分布的概率密度函数
def pdf(x, mean, std_dev):
return norm.pdf(x, mean, std_dev)
# 计算后验概率
def compute_posterior(x):
likelihood_w1 = pdf(x, mean_w1, std_dev_w1)
likelihood_w2 = pdf(x, mean_w2, std_dev_w2)
evidence = (prior_w1 * likelihood_w1) + (prior_w2 * likelihood_w2)
posterior_w1 = (prior_w1 * likelihood_w1) / evidence
posterior_w2 = (prior_w2 * likelihood_w2) / evidence
return posterior_w1, posterior_w2
# 最小错误贝叶斯分类器
def minimum_error_classifier(x):
posterior_w1, posterior_w2 = compute_posterior(x)
if posterior_w1 > posterior_w2:
return "w1"
else:
return "w2"
# 最小风险贝叶斯分类器
def minimum_risk_classifier(x):
posterior_w1, posterior_w2 = compute_posterior(x)
decision_a1 = 0 * posterior_w1 + 6 * posterior_w2
decision_a2 = 1 * posterior_w1 + 0 * posterior_w2
if decision_a1 < decision_a2:
return "a1"
else:
return "a2"
# 生成绘制概率密度函数曲线的x值
x_values = np.linspace(-10, 10, 1000)
# 计算并绘制概率密度函数曲线
plt.plot(x_values, pdf(x_values, mean_w1, std_dev_w1), label='P(x|w1)')
plt.plot(x_values, pdf(x_values, mean_w2, std_dev_w2), label='P(x|w2)')
# 绘制决策界面
plt.axvline(x=0, color='r', linestyle='--', label='Decision Boundary')
# 分类结果示意
for point in data:
class_w1 = minimum_error_classifier(point)
class_w2 = minimum_risk_classifier(point)
plt.scatter(point, 0, color='g' if class_w1 == 'w1' else 'b', marker='o', label=f'Classified as {class_w1}')
plt.scatter(point, 0, color='g' if class_w2 == 'a1' else 'b', marker='x', label=f'Classified as {class_w2}')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.title('Normal Distribution and Bayesian Classification')
plt.legend()
plt.show()
对代码的解释:
-
导入必要的库:
numpy:用于数值计算。matplotlib.pyplot:用于绘图。scipy.stats.norm:用于生成正态分布的概率密度函数。
-
定义了一些数据和参数:
data:给定的观察值列表,这些观察值是细胞识别中正常细胞和异常细胞的观察结果。prior_w1和prior_w2:分别是正常细胞和异常细胞的先验概率。mean_w1、variance_w1和std_dev_w1:正常细胞的类条件概率分布的均值、方差和标准差。mean_w2、variance_w2和std_dev_w2:异常细胞的类条件概率分布的均值、方差和标准差。
-
定义了正态分布的概率密度函数
pdf(x, mean, std_dev),该函数使用scipy.stats.norm.pdf来计算给定均值和标准差的正态分布在给定x值处的概率密度。 -
定义了
compute_posterior(x)函数,该函数计算了给定观察值x下的后验概率。它使用类条件概率分布(正态分布)和先验概率来计算后验概率,并返回正常细胞和异常细胞的后验概率。 -
实现了最小错误贝叶斯分类器
minimum_error_classifier(x),该函数根据后验概率来决定将观察值x分为哪个类别(正常细胞w1或异常细胞w2)。它选择后验概率较大的类别作为分类结果。 -
实现了最小风险贝叶斯分类器
minimum_risk_classifier(x),该函数根据后验概率和提供的决策表来决定将观察值x分为哪个类别(a1或a2)。它根据决策表中的风险值计算,并选择风险较小的类别作为分类结果。 -
生成了绘制概率密度函数曲线的
x_values,该变量在范围-10到10内生成了一系列x值。 -
使用
plt.plot函数绘制了正态分布的概率密度函数曲线,分别绘制了P(x|w1)和P(x|w2)。 -
使用
plt.axvline函数绘制了决策界面,该界面在x=0处画了一条红色虚线,表示分类决策的分界线。 -
使用循环遍历了给定的观察值
data,对每个观察值进行最小错误贝叶斯分类和最小风险贝叶斯分类,并绘制了示意图来表示分类结果。 -
最后,添加了标签、标题和图例,并使用
plt.show()函数显示图形。
这段代码帮助你理解如何基于正态分布的类条件概率分布、先验概率以及风险表来实现最小错误贝叶斯分类器和最小风险贝叶斯分类器,并可视化分类结果。
实验结果:
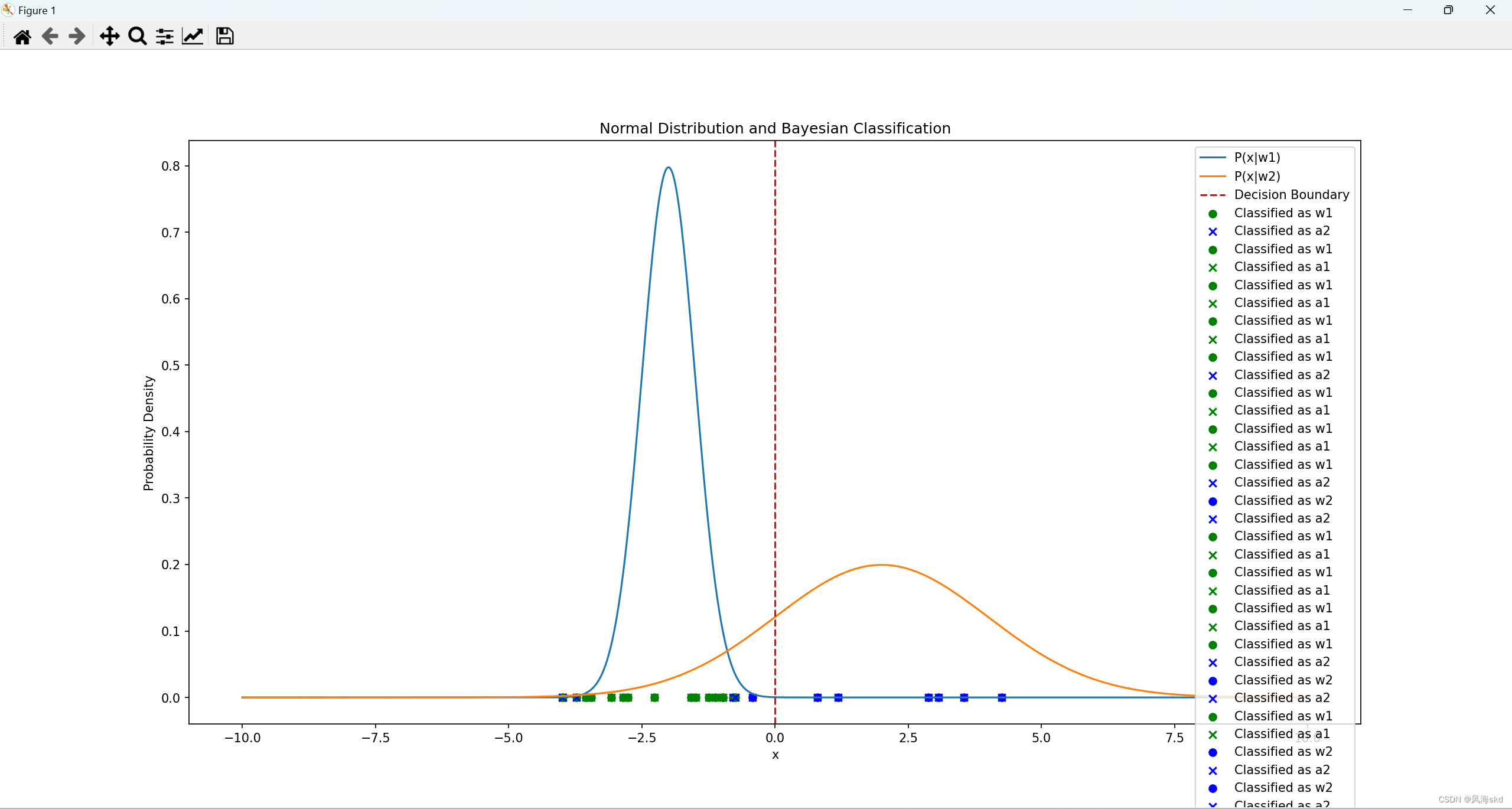







 本文介绍了如何使用Python编程实现基于正态分布的最小错误和最小风险贝叶斯分类器,通过给定数据和参数,计算后验概率并绘制分布曲线和分类结果,同时展示了两种分类方法的区别。
本文介绍了如何使用Python编程实现基于正态分布的最小错误和最小风险贝叶斯分类器,通过给定数据和参数,计算后验概率并绘制分布曲线和分类结果,同时展示了两种分类方法的区别。
















 1266
1266

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








