代码随想录刷题-栈与队列-用栈实现队列

原创已于 2023-04-10 11:05:00 修改 · 386 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #leetcode

于 2023-04-10 10:57:39 首次发布

算法刷题总结专栏收录该内容

39 篇文章

订阅专栏

文章讨论了如何使用两个栈来实现一个队列，包括push、pop、peek和empty操作。作者提供了个人的解法，然后分析了官方的优化方案，强调了在push和pop操作中避免不必要的元素转移，以及简化empty检查的方法。官方解法实现了平均时间复杂度为O(1)的操作，并指出空间复杂度与操作总数成正比。

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：
实现 MyQueue 类：

void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空，返回 true ；否则，返回 false
说明：

你只能使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

输入：
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 1, 1, false]

解释：
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

我的解法

仅作为记录，非最优，可优化

一个栈只能后进先出，如果想实现先进先出那最少要两个栈。我的想法是需要输出的时候将 s1都 push 到 s2中，这样顺序就会反转，从而符合先进先出。当 push 元素的时候再把 s2的元素都 push 到 s1后，再将要 push 的元素放到 s1中，这样不难写出如下代码

class MyQueue {
   public:
    MyQueue() {}

    void push(int x) {
        while (!s2.empty()) {
            s1.push(s2.top());
            s2.pop();
        }
        s1.push(x);
    }

    int pop() {
        if (s2.empty()) {
            while (!s1.empty()) {
                s2.push(s1.top());
                s1.pop();
            }
        }
        int res = s2.top();
        s2.pop();
        return res;
    }

    int peek() {
        if (s2.empty()) {
            while (!s1.empty()) {
                s2.push(s1.top());
                s1.pop();
            }
        }
        int res = s2.top();
        return res;
    }

    bool empty() {
        if (s1.empty() && s2.empty()) {
            return true;
        } else {
            return false;
        }
    }
    stack<int> s1;
    stack<int> s2;
};

官方解法

上面我的解法有几个地方可以优化。

①我每次 push 的时候都将 s2的元素 push 到 s1中。其实不必这样做，我们将 s2作为输出栈，s1作为输入栈，s2专门用于输出。s2不为空的时候那 pop 的时候直接 pop s2就行，而 s2为空时，再将 s1的元素都 push 到 s2中

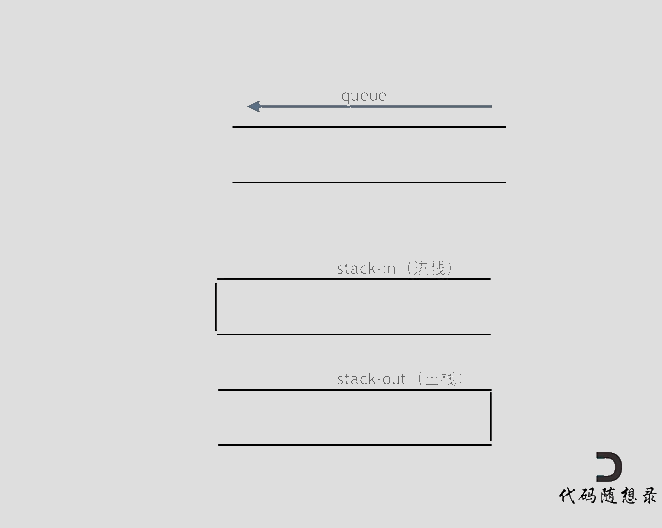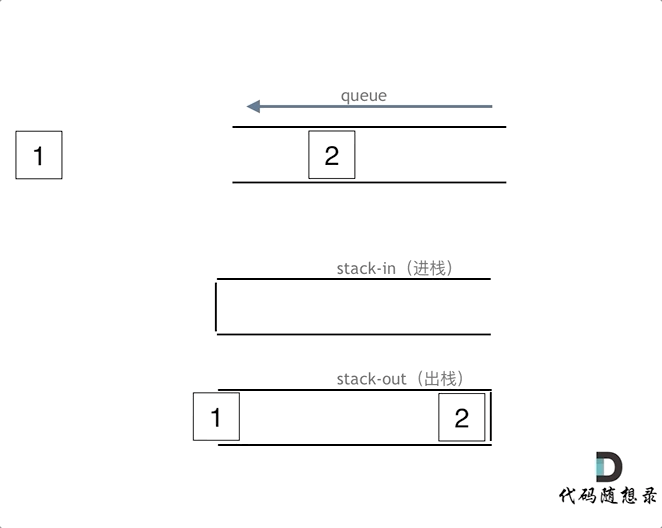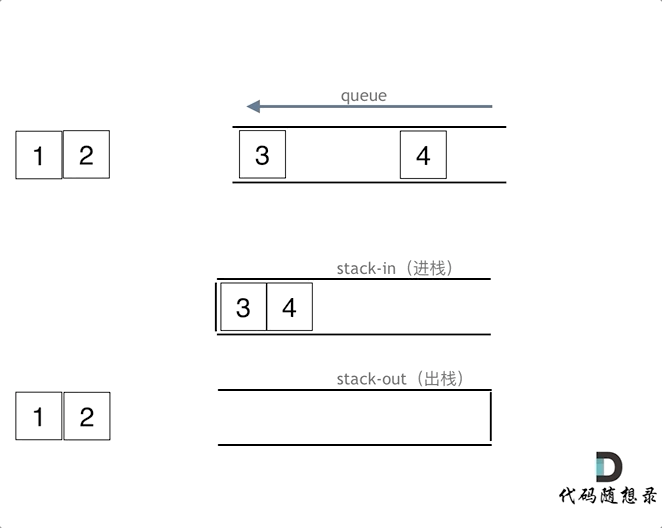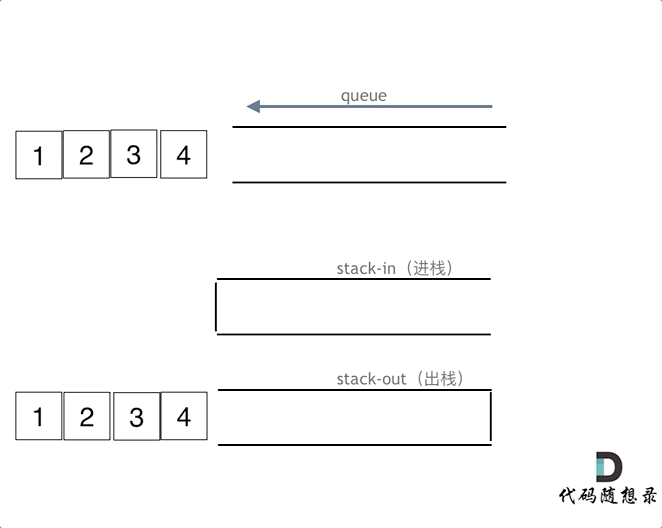
请添加图片描述

②peek 和 pop 类似，只不过 peek 不用 pop 元素，我的解法中重复写了一遍代码，但更好的写法是封装成一个函数，调用函数；或者利用写好的 pop 函数，pop 后再 push 之前 pop 的元素

③判断是否为空的时候，直接 return s1.empty() && s2.empty(); 即可，这样更简洁

class MyQueue {
private:
    stack<int> inStack, outStack;
    // 封装成函数
    void in2out() {
        while (!inStack.empty()) {
            outStack.push(inStack.top());
            inStack.pop();
        }
    }

public:
    MyQueue() {}

    void push(int x) {
        inStack.push(x);
    }

    int pop() {
        if (outStack.empty()) {
            in2out();
        }
        int x = outStack.top();
        outStack.pop();
        return x;
    }

    int peek() {
        if (outStack.empty()) {
            in2out();
        }
        return outStack.top();
    }

    bool empty() {
        return inStack.empty() && outStack.empty();
    }
};