归并排序

归并排序

一、时间复杂度

    稳定排序算法 O(n log n)

 

二、归并排序基本思路

    归并排序主要的操作是通过递归将数据集拆分成最小集合，也就是单个数，然后从最小集合开始往上递归合并。如其名，递归分解数据及，然后将拆分后的数据及归结。

如下图（图片资源，算法资源来源于:https://zhuanlan.zhihu.com/p/36075856）

    

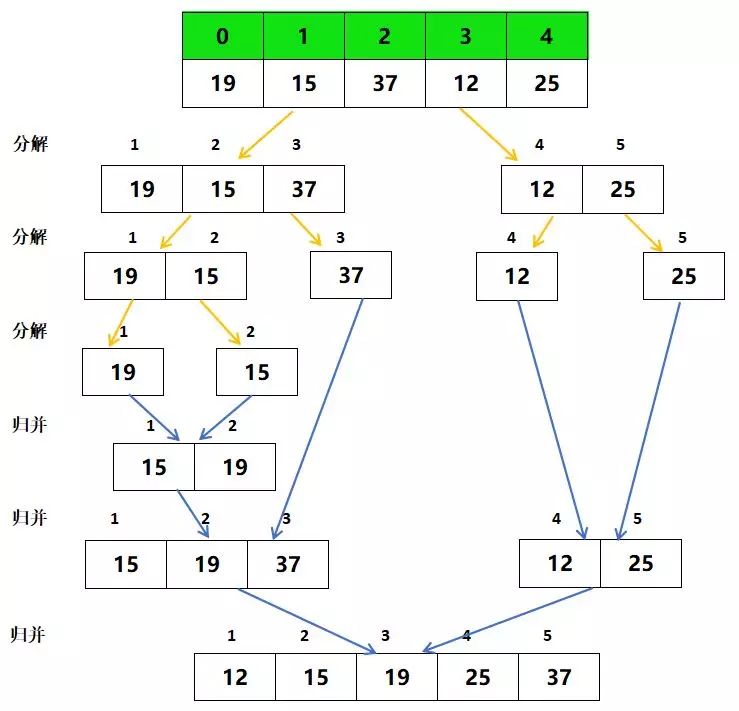
动态图

具体算法解析

public static void mergeSortSum(int[] unsortedList){
        int[] temp = new int[unsortedList.length];
        mergeSort(unsortedList, 0, unsortedList.length - 1, temp);
    }

    public static void mergeSort(int[] unsortedList, int left, int right,int[] temp){
        if(left < right){
            int mid = (left + right)/2;//用于切割数据及
            mergeSort(unsortedList, left, mid, temp); // 递归拆分左边集合
            mergeSort(unsortedList, mid + 1, right, temp); //递归拆分右边集合
            mergeArray(unsortedList, left, mid, right, temp); // 将左右子集合合并
        }
    }

    private static void mergeArray(int array[], int first, int mid, int last, int temp[]) {
        int arrayLeftStartIndex = first, arrayRightStartIndex = mid + 1; // arrayLeftStartIndex为左边集合起点, arrayRightStartIndex为右边的起点
        int arrayLeftEndIndex = mid, arrayRightIndex = last; // arrayLeftEndIndex为左边集合的终点, arrayRightIndex为右边集合的终点
        int k = 0; // k用于指向temp数组当前放到哪个位置
        while (arrayLeftStartIndex <= arrayLeftEndIndex && arrayRightStartIndex <= arrayRightIndex) { // 将两个有序序列循环比较, 填入数组temp
            if (array[arrayLeftStartIndex] <= array[arrayRightStartIndex])
                temp[k++] = array[arrayLeftStartIndex++];
            else
                temp[k++] = array[arrayRightStartIndex++];
        }
        // 如果比较完毕, 第一组还有数剩下, 则全部填入temp
        while (arrayLeftStartIndex <= arrayLeftEndIndex) {
            temp[k++] = array[arrayLeftStartIndex++];
        }
        // 如果比较完毕, 第二组还有数剩下, 则全部填入temp
        while (arrayRightStartIndex <= arrayRightIndex) {
            temp[k++] = array[arrayRightStartIndex++];
        }
        //由于顺序是从左到右归并，所以不会被覆盖掉，
        for (arrayLeftStartIndex = 0; arrayLeftStartIndex < k; arrayLeftStartIndex++) {
            array[first + arrayLeftStartIndex] = temp[arrayLeftStartIndex];
        }
    }