2023HBCPC补题A Solution Preparation

解题思路：

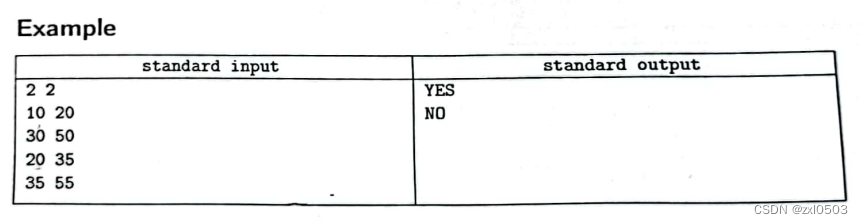
题目意思是有n种水，每个水里包含A和C两种溶质，会给你n种水每杯水的AC溶质含量，每种水不限制杯数，然后让你求是否可以兑出包含目标溶质Qa和Qc的水。

这里以Ai和Ci作为横纵坐标建立坐标系，已给出的水的Ai和Ci作为点，去求已经有的点的凸包（所能围成的最大面积）；

对于求出的凸包顶点，可以组成多边形。需要判断的就是点（Qa，Qc）是否在多边形内部，如果在多边形内部，则可以用已有的水调制出来，反之不行。

代码参考：

#include <bits/stdc++.h>

using namespace std;

const double pi=acos(-1.0);
const double eps=1e-8;

int m;

int sgn(double x){
	if(fabs(x)<eps){
		return 0;
	}
	else{
		return x<0?-1:1;
	}
}

struct Point{
	double x,y;
	Point(){
		
	}
	Point(double x,double y):x(x),y(y){
	}
	Point operator+(Point B){
		return Point(x+B.x,y+B.y);
	}
	Point operator-(Point B){
		return Point(x-B.x,y-B.y);
	}
	Point operator*(double k){
		return Point(x*k,y*k);
	}
	Point operator/(double k){
		return Point(x/k,y/k);
	}
	bool operator == (Point B){
		return sgn(x-B.x)==0&&sgn(y-B.y)==0;
	}
};

typedef Point Vector;

double Cross(Vector A,Vector B){
	return A.x*B.y-A.y*B.x;
}

struct Line{
	Point p1,p2;
	Line(){
	}
	Line(Point p1,Point p2):p1(p1),p2(p2){
	}
	Line(Point p,double angle){
		p1=p;
		if(sgn(angle-pi/2)==0){
			p2=(p1+Point(0,1));
		}
		else{
			p2=(p1+Point(1,tan(angle)));
		}
	}
	Line(double a,double b,double c){
		if(sgn(a)==0){
			p1=Point(0,-c/b);
			p2=Point(1,-c/b);
		}
		else if(sgn(b)==0){
			p1=Point(-c/a,0);
			p2=Point(-c/a,1);
		}
		else{
			p1=Point(0,-c/b);
			p2=Point(1,(-c-a)/b);
		}
	}
};

double Dot(Vector A,Vector B){
	return A.x*B.x+A.y*B.y;
}

bool Point_on_seg(Point p,Line v){
	return sgn(Cross(p-v.p1,v.p2-v.p1))==0&&sgn(Dot(p-v.p1,p-v.p2))<=0;
}

bool Point_in_polygon(Point pt,Point *p,int n){
	for(int i=0;i<n;i++){
		if(p[i]==pt){
			return true;
		}
	}
	
	for(int i=0;i<n;i++){
		Line v=Line(p[i],p[i+1%n]);
		if(Point_on_seg(pt,v)){
			return true;
		}
	}
	
	int num=0;
	for(int i=0;i<n;i++){
		int j=(i+1)%n;
		int c=sgn(Cross(pt-p[j],p[i]-p[j]));
		int u=sgn(p[i].y-pt.y);
		int v=sgn(p[j].y-pt.y);
		if(c>0&&u<0&&v>=0){
			num++;
		}
		if(c<0&&u>=0&&v<0){
			num--;
		}
	}
	if(num!=0){
		return true;
	}
	return false;
}

int orientation(Point p, Point q, Point r)
{
    int val = (q.y - p.y) * (r.x - q.x) -
              (q.x - p.x) * (r.y - q.y);
  
    if (val == 0) return 0;
    return (val > 0)? 1: 2;
}

void convexHull(Point points[], int n)
{
	
    //if (n < 3) return;
  
    vector<Point> hull;//存储凸包顶点集合； 
  
    int l = 0;
    for (int i = 1; i < n; i++)
        if (points[i].x < points[l].x)
            l = i;
  
    int p = l, q;
    do
    {
        hull.push_back(points[p]);
        q = (p+1)%n;
        for (int i = 0; i < n; i++)
        {
           if (orientation(points[p], points[i], points[q]) == 2)
               q = i;
        }
        p = q;
  
    } while (p != l);
    Point ps[105];
    for (int i = 0; i < hull.size(); i++){
    	ps[i].x=hull[i].x;
    	ps[i].y=hull[i].y;
	}
    Point Qas;
    //cout<<m<<endl;
    while(m--){
    	cin>>Qas.x>>Qas.y;
    	if(Point_in_polygon(Qas,ps,hull.size())){
			cout<<"YES"<<endl;
		}
		else{
			cout<<"NO"<<endl;
		}
    	
	}
    
    
    /*for (int i = 0; i < hull.size(); i++)
        cout << "(" << hull[i].x << ", "<< hull[i].y << ")\n";*/
}

int main(){
	int n;
	cin>>n>>m;
	Point points[105];
	for(int i=0;i<n;i++){
		cin>>points[i].x>>points[i].y;
	}
    convexHull(points, n);
	return 0;
}