BB-RO 方案 在随机谕言机模型下的安全证明

BB-RO 方案 在随机谕言机模型下的安全证明

密码学可证明安全推荐书目（系列博客内容为这两本书学习笔记与内容小结):

《密码学中的可证明安全性》杨波 清华大学出版社

《Introduction to Security Reduction》Fuchun Guo;Willy Susilo;Yi Mu Springer

BB_RO 方案描述

系统初始化阶段：

                           

         系统初始化阶段与BLS 协议相同。

秘钥生成阶段：

                             

         秘钥生成阶段，私钥为整数群上选取的一个随机数，公钥为一个二元组（g1,g2）其中g2 是群上的一个随机生成元素。

签名阶段：

                               

         签名阶段，签名分为两个部分，第一个部分，为使用私钥对签名的哈希值进行签名。第二部分，为岁随机数r的运算，此处可以看做是对随机数r的隐藏。

验证阶段：

                             

安全证明：

定理 ： 如果BBRO协议中的哈希函数是随机谕言机，并且CDH假设是困难的，那么BBRO协议在EU-CMA模型下是可证明安全的，规约损失 L= qH，其中qH 为哈希询问的次数。

要证明这个定理，实质上就需要设计一个合理的安全规约算法，其中设置模拟者给与敌手的签名是可模拟的，敌手伪造的签名是可规约的。而实现这个功能的途径就是将随机谕言机，通过对随机谕言机进行编程，是的敌手获得的哈希询问结果只能计算出可规约签名，模拟者查询哈希询问结果并且计算得到的签名只能计算出可模拟签名。

一般来说，常用的随机谕言机编程如下：

                                                                     

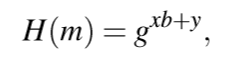
对于CDH假设下的数字签名，这个范式比较常用，已知 g，g^a，g^b，求g^ab。

x 可以控制b的存在与否，y 是随机值，为了保证随机谕言机每次返回的值都是独立随机的。

                                  

将公钥，设置为CDH的前置条件，a 为私钥。敌手不知道私钥，给与敌手一个CDH问题实例。

                                 

                                 

敌手请求哈希询问，模拟者构建一个哈希列表，并且设定第i次敌手请求的消息是mi, 也就是说，模拟者提前猜测敌手会在这一次发动伪造签名攻击。根据敌手询问的次数，分别设计随机谕言机给与敌手的回复。注意，第i次请求敌手将会产生可规约签名，其他情况下，模拟者输出可模拟签名，敌手不能分辨是可模拟的还是真实签名。

                                   

签名询问，如果敌手询问第i次签名，则模拟者中断，因为不允许敌手询问伪造签名的消息。模拟者随机选择一个r`,然后反向表示r` ,得到算法形式上的随机数r。与之前说到的签名不同，这个设计就比较复杂了。最后得到可模拟的签名。

                                    

伪造签名，当敌手选择第i次的消息M*做完哈希询问后，随机伪造这个消息的签名，得到一个可规约的签名。

敌手的优势为1\qh *adv , 证明完毕。

一个思考：

如何构建规约？从现在来看，其实安全规约就是在凑参数，通过精心设计规约算法的参数，构建一种闭环、自洽的证明逻辑。在Guo Fuchun 的书中，他简单的将随机谕言机下安全规约做了三个分类 分别是H型 I型 C型。那么，为什么要分成这几种类型呢？这几种类型应该是比较常见的，但是在实际设计安全规约的过程中，必须根据实际情况来选择参数的变化，例如 H型 和 I型的区别就是公钥中包含的困难问题条件信息不同，在设计安全规约时的参数考量就会不同。