向量数据库原理

向量数据库定义：专门用于存储和管理向量数据的数据库，能对向量数据进行高效的操作，包括增删改查。

向量数据库相比传统数据库，有如下特点：

1、数据规模超过传统的关系型数据库，数据规模通常超过10亿，单数据向量纬度常超过1000维*float，存储空间需求大。

2、查询方式不同，计算密集型，传统数据库要求精确查询，向量数据库查找相似结果。

3、向量数据库要求时延小，通常亿级数据要求在1s内。

一、Product Quantization

1、将数据集按纬度划分成一个一个的小维度。

假设有n=50,000由1024维的数据。那么整个数据集集由50000*1024的向量来表示。然后我们把1024维的向量平均分成m=8（实验标明最佳的数）个子向量，每组子向量128维。如下图：

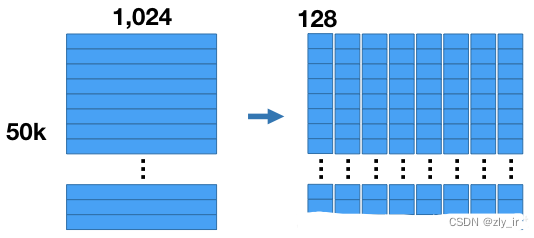
2、使用k-means算法，聚类成k个类别，k一般为256（实验标明）。

 

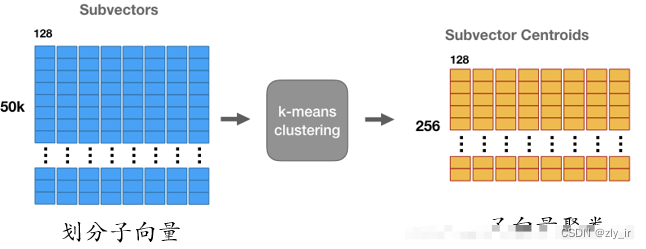
3、向量压缩，在product quantization方法中，这256个中心点构成一个码本。这些码本的笛卡尔积就是原始D维向量对应的码本。用qj表示第j组子向量，用[Cj表示其对应学习到的聚类中心码本，那么原始D维向量对应的码本就是C=C1×C2×…×Cm，码本大小为km。 注意到每组子向量有其256个中心点，我们可以用中心点的 ID 来表示每组子向量中的每个向量。中心点的 ID只需要 8位来保存即可。这样，初始一个由32位浮点数组成的1,024维向量，可以转化为8个8位整数组成。

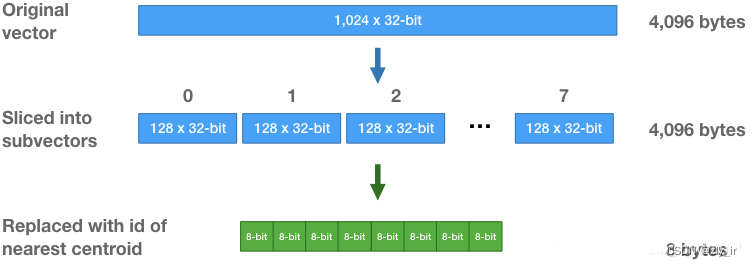
二、最近邻搜索方式

 

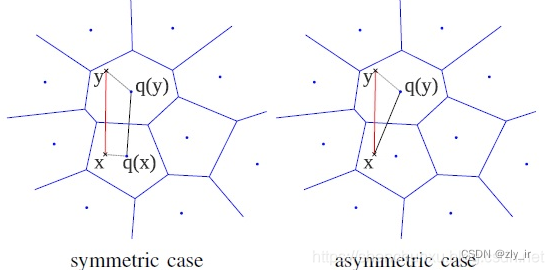
1、SDC(symmetric distance computation)

先用PQ量化器对x和y表示为对应的中心点q(x)和q(y)，然后用下面公式来近似d(x,y)。这里 q 表示 PQ量化过程。

2、ADC(asymmetric distance computation)

只对y表示为对应的中心点q(y)，然后用下述公式来近似d(x,y)

 

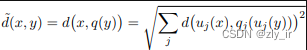
SDC算法和ADC算法的区别在于是否要对查询向量x做量化。如下图所示，x是查询向量(query vector)，y是数据集中的某个向量，目标是要在数据集中找到x的相似向量。

faiss(2)：理解product quantization算法-优快云博客

三、检索加速

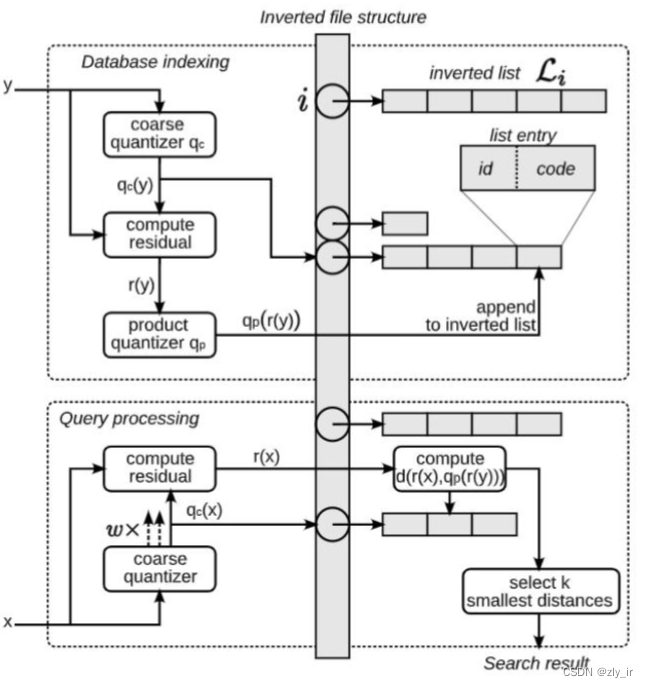
为了能处理千万甚至亿级别的查询，需要使用倒排索引加快查询。

该算法先将N个向量使用k-means聚成 k′ 个类，每个类均用聚类中心向量表示，然后计算原始向量与其所在聚类中心向量的残差向量，使用上文PQ量化器对该残差向量编码，并将编码后的结果挂在原始向量所在的类目ID的倒排链上。

在第一步聚类过程中，邻近的两个向量不一定会落在同一个簇中，因此为提高召回率，我们在检索时会从 w 个簇中进行检索，查询向量 x 的检索过程如下：

• 查找向量 x 最近的 w 个聚类中心

• 对每个聚类中心，计算查找向量与聚类中心的残差向量

• 遍历每个聚类中心的倒排链，按照上节ADC算法计算查询向量与倒排链上候选向量的距离，取距离最小的top k个

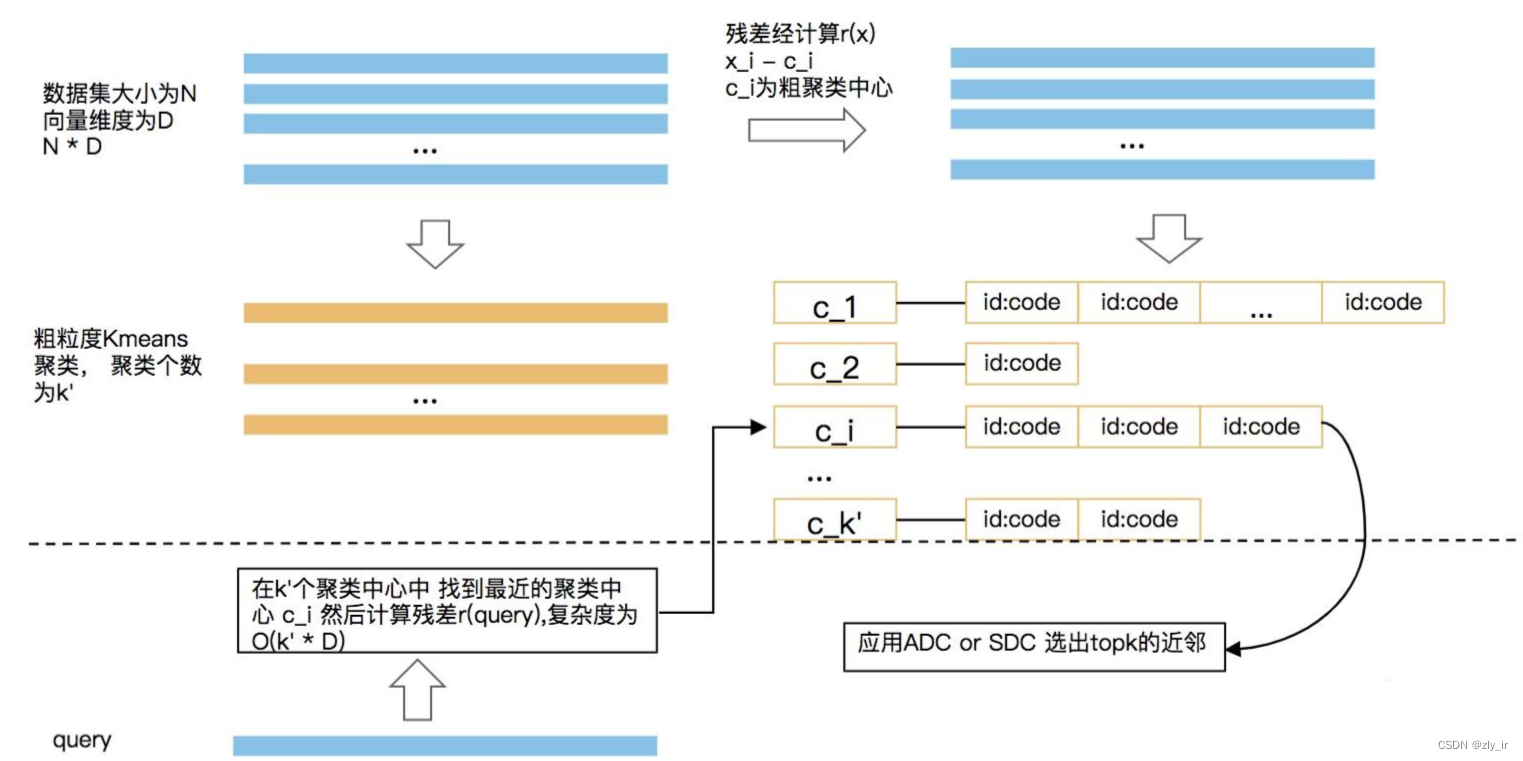
假设倒排链是平衡的，倒排检索时会在 N/k′∗w 个候选集合中进行检索，不使用倒排时的候选集合是 N 。

检索准确率与参数 k′ 和 w 相关，当 k′ 相同时， w 越大准确率越高，当 w 相同时， k′ 越小准确率越高。

faiss原理（Product Quantization）