动态规划-走台阶和国王与金矿问题

（1）、走台阶

有一座N级的台阶，从下往上走，每次走一个或两个台阶，那么走上N阶总共需有多少种方法？

考虑：假设台阶一共10级，那么只差最后一步就走到10级台阶，这时有几种情况？

有两种：第一种，从第9级到第10级；第二种从第8级到第10级。那么现在想想，不管之前0级-9级或者0级-8级走台阶的过程，最后一步肯定是从第9级或者第8级台阶走，假设从0级-8级台阶的走法有X种，0级-9级台阶的走法有Y种，那么从0级-10级台阶有多少种？

分析：10级的台阶走法可以根据最后一步的不同而分为两个部分：第一部分就是最后一步从第9级到第10级，这一部分的走法数量和0级-9级的走法数量是一样的；第二部分最后一步就是从第8级到第10级，它的走法数量和0级-8级是一样的，那么就有如下的关系：X+Y  => F(10) = F(9) + F(8)。将思路画出来，如下图（借鉴小灰图）：

                          

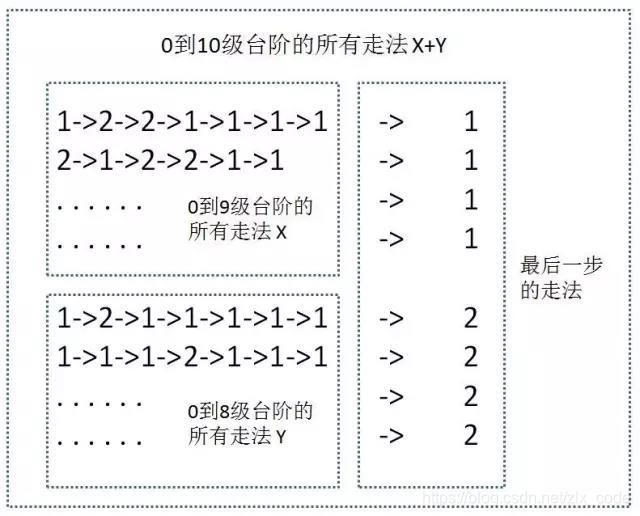
那么我们可以推出递归公式：

，边界条件：

动态规划中包含三个重要的概念：最优子结构、边界和状态转移公式。

下面使用两种方式来实现这个动态规划问题，（由于递归比较简单，这里就不实现了）

1、使用备忘录算法，将计算的中间结果保存在一个HashMap中。若第一次出现的计算值，写入HashMap中；若出现多次，那么直接从map中取出即可，避免重复计算，代码如下：

/**
 *  使用备忘录算法求解
 *  为了避免重复运算，使用一个Map来计算中间结果，若第一次出现则存入Map；
 *  若后面多次出现，那么就直接从Map中取出来，避免重复计算。
 * @param n
 * @return
*/
public static int getClimbingWays(int n, HashMap<Integer, Integer> recordMap){
   // 判断边界条件
   if(n < 0){
      return 0;
   }
   if(n == 1){
      return 1;
   }
   if(n == 2){
      return 2;
   }

   if(recordMap.containsKey(n)){
       return recordMap.get(n);
   }else{
       int value = getClimbingWays(n - 1, recordMap) + getClimbingWays(n - 2, recordMap);
       recordMap.put(n , value);
       return value;
   }
}

2、使用迭代的方式

通过分析我们发现，F(n)的值只和前两个值有关，F(n-1)和F(n-2)，那么我们只需要保存前两个值就可以得到最新的值。代码如下：

/**
 *   分析：
 *   台阶数： 1    2    3    4   ...
 *   走法数： 1    2    3    5   ...
 *   台阶个数1和2的走法数是边界值，台阶数3的走法数，是1和2的和；
 *   而台阶数4的走法数是2和3的和，台阶数3的走法数只依赖1和2；
 *   台阶数4的走法数只依赖2和3。每次迭代的过程中，只依赖前两个状态，
 *   就可以得到最新的状态，因此只需保留前两次的状态即可。
 */
 public static int getClimbingWays(int n){
    if(n < 0 ) {
        return 0;
    }
    if(n == 1){
        return 1;
    }
    if(n == 2){
        return 2;
    }
    // 迭代
    // 前两个值
    int a = 1;
    int b = 2;
    // 当前值
    int current = 0;
    for (int i = 3; i <= n ; i++) {
        current = a + b;
        a = b;
        b = current ;
    }
    return current;
 }

（2）、国王和金矿

题目：有一个国家发现了5座金矿，每座金矿的黄金储备量不同，需要参与的挖掘的工人数也不同。参与挖掘工人总数是10人。每座金矿要么全挖要么不挖，不能派出一半人挖取一半金矿。求解要得到尽可能多的黄金，应该挖取哪几座金矿？比如5座金矿总量和用工数如下：400金/5人，500金/5人，200金/3人，300金/4人，350金/3人。

分析：10人5金矿的最优子结构是10人4金矿时对应的最优子结构。10人4金矿最优结果有两种可能，一种是：第5座金矿不挖，只挖前4座金矿；还有就是第5座金矿挖，那么前4座金矿所需的人数就是10-第5座金矿的人数。那么4座金矿的最优选择对应5座金矿的最优选择就是：前4座金矿10人挖金数量与前4座挖金数量+第5座金矿挖金数量中的最大值，如下图所示（借鉴小灰图）：

              

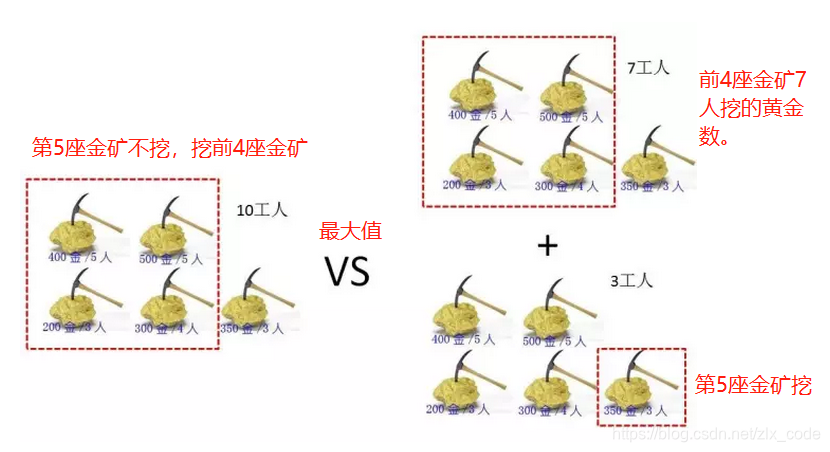
假设金矿数量N，工人数W，金矿的黄金量为G[]，金矿用工数P[]，通过上述分析，我们可以得知5金矿和4金矿的最优选择存在如下关系：

                                 

上述就是状态转移方程，那么边界就是：

当 N = 1，W >= P[0] 时， F(N, W) = G[0];

当 N = 1，W < P[0] 时， F(N, W) = 0

通过整理可得如下状态转移方程：

                    

借助如下表格帮助写出迭代方式的代码（拷贝自小灰图）：

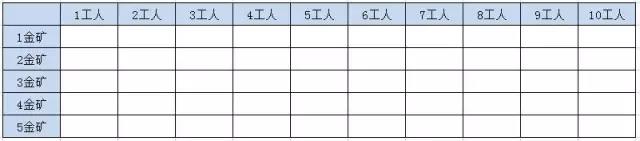
表格第一行是工人数，第二行是金矿数。第一座金矿数是400金/5人，那么可以填写第一行的值：

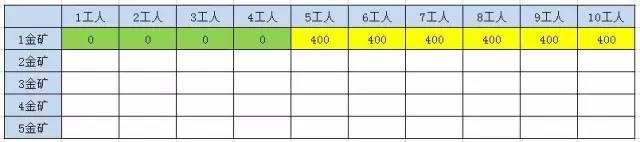
同理第二行，注意最后一个值的填写， F(2,10) = max(F(1, 10),   F(1, 10 - 5) + G[1])  => F(2,10) = max(400,  400 + 500) = 900，因此是900。

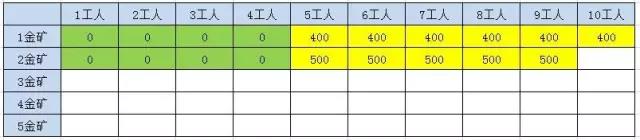
同理可以得到如下所以的数量信息：

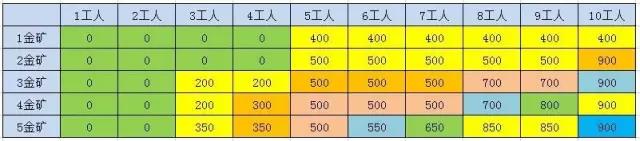
找规律：比如第3座金矿8工人的结果，就是2金矿5工人和 2金矿8工人来的 F(3, 8) = max( F(2, 8), F(2, 5) + G[2])

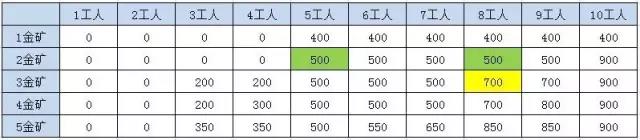
可以看出我们只需要存储前一行的结果就可以得到下一行的结果，而不需要存储前面的所有表格。

    /**
     * @param n   金矿数
     * @param w   工人数
     * @param g   每个金矿对应的黄金数
     * @param p   每个金矿对应的用工数
     * @return
     */
    public static int getMostGold(int n, int w, int[] g, int[] p){
        // 存储前一次的结果
        int[] preResult = new int[p.length];
        // 存储当前结果
        int[] results = new int[p.length];
        // 填充边界，表格第一行结果
        for (int i = 0; i <= w ; i++) {
            if(i < p[0]){
                preResult[i] = 0;
            }else{
                preResult[i] = p[0];
            }
        }

        // 填充其余的格子
        // 外层循环是金矿数量，内存循环是工人数
        for (int i = 0; i < n; i++) {
            for (int j = 0; j <= w ; j++) {
                if(j < p[i]){
                    results[j] = preResult[j];
                }else{
                    // 根据迭代公式
                    results[j] = Math.max(preResult[j], preResult[j-p[i]] + g[i]);
                }
            }
            preResult = results;
        }
        return results[n];
    }