腾讯3-最长回文子串

腾讯3-最长回文子串leetcode5

思路：回文的标准做法就是dp

dp[i][j]的状态取决于i和j位置上是否相等，以及dp[i+1][j-1]的状态
因为dp[i][j]需要提前已知[j-1]的状态，而且i必然小于j，
所以循环是第一层for先固定j,然后第二层for 的i从0遍历到j.

其中f(i,j)表示当s[i:j]子串是否是回文串。
当j-i<=1时，只有两个字符的时候，如果s[i] == s[j]则表示s[i:j]为回文串，即f(i,j) = true，否则f(i,j) = false。
当j-i > 1时，大于两个字符的时候，则判断 s[i]、s[j]是否相等以及f(i+1, j-1)是否为true，即s[i+1:j-1]是否为回文串，如果为真，则f(i,j) = true

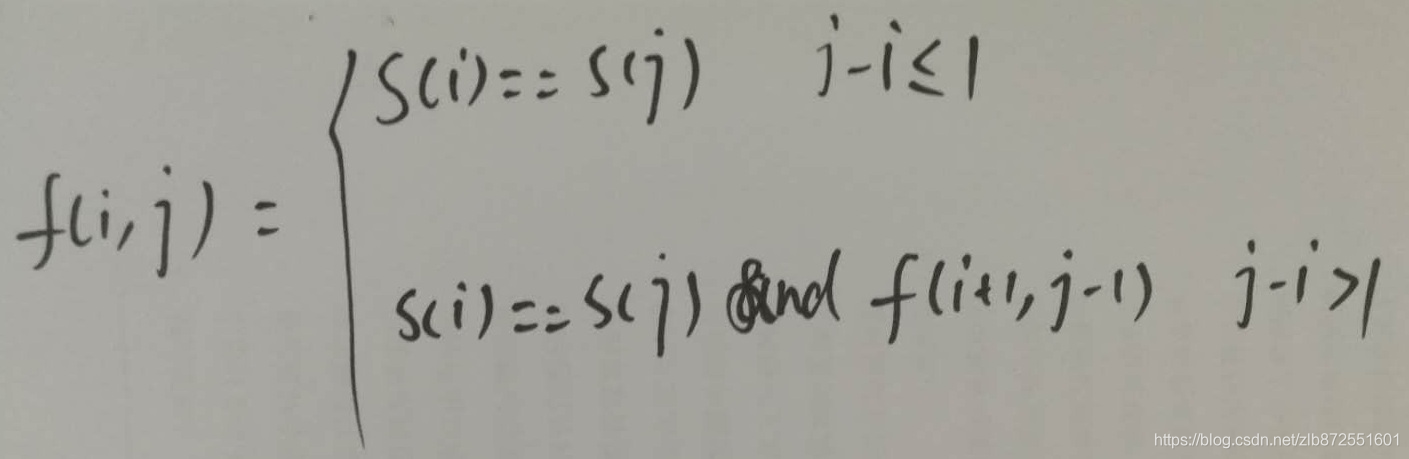
所以就需要一个n*n的二维矩阵用于存储f(i,j)的值，其中 j in range(0, k)，i in range(0, j+1)，之所以是j+1是因为i可以等于j。

class Solution:
    def longestPalindrome(self, s: str) -> str:
        k=len(s)
        matrix=[[0 for i in range(k)] for i in range(k)]# 初始化n*n的列表
        longestsubstr=''# 存储最长回文子串
        longestlen=0# 最长回文子串的长度
 
        for j in range(0, k):
            for i in range(0, j+1):
                if j - i <= 1:
                    if s[i] == s[j]:
                        matrix[i][j]=1# 此时f(i,j)置为true 
                        if longestlen <j-i+1:# 将s[i:j]的长度与当前的回文子串的最长长度相比
                            longestsubstr=s[i:j+1]# 取当前的最长回文子串

                            longestlen = j - i + 1   # 当前最长回文子串的长度
                else:
                    if s[i] ==s[j] and matrix[i+1][j-1]:# 判断
                        matrix[i][j]=1
                        if longestlen < j - i + 1:
                            longestsubstr = s[i:j+1]
                            longestlen = j - i + 1
        return longestsubstr