POJ 1328

Radar Installation Time Limit: 1000MS   Memory Limit: 10000K Total Submissions: 44134   Accepted: 9774 Description Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.  We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates. 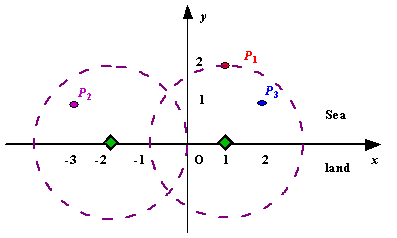   Figure A Sample Input of Radar Installations Input The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.  The input is terminated by a line containing pair of zeros  Output For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case. Sample Input 3 2 1 2 -3 1 2 1 1 2 0 2 0 0 Sample Output Case 1: 2 Case 2: 1 Source Beijing 2002

一道挺经典的贪心。每个点可以在x轴覆盖一个区间，然后按x从小到大排序 ， 找重叠区域即可。

#include <cstdio>
#include <cmath>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <map>
#include <string>
#include <stack>
#include <cctype>
#include <vector>
#include <queue>
#include <set>
#include <utility>
#include <cassert>
using namespace std;
///#define Online_Judge
#define outstars cout << "***********************" << endl;
#define clr(a,b) memset(a,b,sizeof(a))
#define lson l , m  , rt << 1
#define rson m + 1 , r , rt << 1 | 1
#define mk make_pair
#define FOR(i , x , n) for(int i = (x) ; i < (n) ; i++)
#define FORR(i , x , n) for(int i = (x) ; i <= (n) ; i++)
#define REP(i , x , n) for(int i = (x) ; i > (n) ; i--)
#define REPP(i ,x , n) for(int i = (x) ; i >= (n) ; i--)
const int MAXN = 1000 + 50;
const int sigma_size = 26;
const long long LLMAX = 0x7fffffffffffffffLL;
const long long LLMIN = 0x8000000000000000LL;
const int INF = 0x7fffffff;
const int IMIN = 0x80000000;
#define eps 1e-8
const int MOD = (int)1e9 + 7;
typedef long long LL;
const double PI = acos(-1.0);
typedef double D;
typedef pair<int , int> pi;
///#pragma comment(linker, "/STACK:102400000,102400000")
struct Point
{
    D x , y;
}a[MAXN];
bool cmp(Point a , Point b)
{
    return a.x < b.x;
}

int main()
{
//    freopen("heritage.in","r",stdin);
//    freopen("heritage.out","w",stdout);
    int n , d;
    int kase = 1;
    while(~scanf("%d%d" , &n , &d)&&(n || d))
    {
        printf("Case %d: " , kase++);
        int ok = 1;
        FOR(i , 0 , n)
        {
            int xxx , yyy;
            scanf("%d%d" , &xxx , &yyy);
            if(abs(yyy) > d)ok = 0;
            a[i].x = xxx * 1.000 - sqrt(d * d * 1.000 - yyy * yyy * 1.000);
            a[i].y = xxx * 1.000 + sqrt(d * d * 1.000 - yyy * yyy * 1.000);
        }
        if(!ok)printf("-1\n");
        else
        {
            sort(a , a + n , cmp);
            int cnt = 1;
            D tmp = a[0].y;
            FOR(i , 1, n)
            {
                if(a[i].y < tmp)
                {
                    tmp = a[i].y;
                }
                else if(a[i].x > tmp)
                {
                    cnt++;
                    tmp = a[i].y;
                }
            }
            printf("%d\n" , cnt);
        }
    }
    return 0;
}