【leetcode】119 杨辉三角II（迭代）

最新推荐文章于 2022-07-19 21:52:14 发布

zjwreal

最新推荐文章于 2022-07-19 21:52:14 发布

阅读量181

点赞数

CC 4.0 BY-SA版权

分类专栏： LeetCode 文章标签：迭代

本文链接：https://blog.youkuaiyun.com/zjwreal/article/details/94487802

LeetCode 专栏收录该内容

297 篇文章

订阅专栏

本文探讨了如何求解杨辉三角的第K行，提供了两种算法实现，一种使用临时数组进行迭代，另一种采用原地更新数组的方式，实现了O(k)的空间复杂度优化。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接：https://leetcode-cn.com/problems/pascals-triangle-ii/

题目描述

给定一个非负索引 k，其中 k ≤ 33，返回杨辉三角的第 k 行。

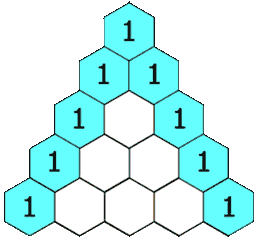
在这里插入图片描述

在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:

输入: 3
输出: [1,3,3,1]

进阶：

你可以优化你的算法到 O(k) 空间复杂度吗？

代码

class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> ret;
        if(rowIndex < 0) return ret;
        ret.push_back(1);
        if(rowIndex == 0) return ret;
        ret.push_back(1);
        if(rowIndex == 1) return ret;
        for (int i = 2; i <= rowIndex; ++i) {
            vector<int> tmp = {1};
            for (int j = 1; j < ret.size(); ++j)
                tmp.push_back(ret[j]+ret[j-1]);
            tmp.push_back(1);
            ret = tmp;
        }
        return ret;
    }
};

在这里插入图片描述
关键是从后往前，类似错位相加

class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> res(rowIndex+1,0);
        res[0]=1;
        for(int i=1;i<rowIndex+1;i++)
        {
            for(int j=i;j>=1;j--)
                res[j]+=res[j-1]; // 从后往前
        }
        
        return res;
    }
};

在这里插入图片描述