带着canvas去流浪系列之三绘制饼图

最新推荐文章于 2020-12-31 12:34:59 发布

原创最新推荐文章于 2020-12-31 12:34:59 发布 · 56 阅读

0 ·

CC 4.0 BY-SA版权

本文介绍如何使用原生canvas API绘制南丁格尔玫瑰图，通过计算扇区角度和半径，实现在Echarts中常见的图表样式。文章提供详细算法步骤及示例代码。

【摘要】用canvas原生API绘制Echarts图表

示例代码托管在：http://www.github.com/dashnowords/blogs

一. 任务说明

使用原生canvasAPI绘制饼图(南丁格尔玫瑰)。(截图以及数据来自于百度Echarts官方示例库【查看示例链接】)。

二. 重点提示

南丁格尔玫瑰图的画法有很多种，Echarts中提供的以半径或面积两种不同模式，本文中以面积比例画法为例，绘制算法如下：

确定每个扇区的角度。由于所有扇区的角度加在一起为2π ，我们先按照数据比例来计算角度：
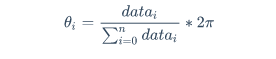
每个扇区面积与总面积之间的比例即为数值的比，将给定参数数组options.radius中的最大和最小数值作为数值最大的一块扇形的绘图数据，代入如下公式即可求得总面积S：

3. 再利用上述公式分别计算出每个扇形对应的外圆半径，在canvas中绘制路径并填充即可。

三. 示例代码

南丁格尔玫瑰图绘制示例代码：

//绘制饼图
drawPieChart(options);
   
/**
* 绘制饼图
* @param  {[type]} options [description]
* @return {[type]}         [description]
*/
function drawPieChart(options) {
  //记录最大数值以反求面积总和
  options.maxValue = 0;
  //求数据集总和以在后续计算每个扇形的角度比例
  options.totalNum = options.data.reduce((pre,cur)=>{
    if (cur.value > options.maxValue) {
        options.maxValue = cur.value;
    }
    return pre+cur.value;
  },0);
   /*以最大值对应最大半径来计算面积总和，并覆盖原值
   *使得最大的一块扇形外圆半径为options.radius[0]
   *内圆半径为options.radius[1]
   */
   let Rmin = options.radius[0];
   let Rmax = options.radius[1];
   let r = Math.sqrt((Rmax*Rmax - Rmin*Rmin)*options.totalNum / options.maxValue + Rmin*Rmin);
   options.radius[1] = r;
   //移动坐标系原点至绘图中心
  let paintingCenter={
    x:parseInt(options.center[0],10)/100 * (options.chartZone[2] - options.chartZone[0]) + options.chartZone[0],
    y:parseInt(options.center[1],10)/100 * (options.chartZone[3] - options.chartZone[1]) + options.chartZone[1]
  }
  context.translate(paintingCenter.x, paintingCenter.y);
   //绘制每个扇形,过程中累加旋转角度
  let allAngle = options.data.reduce((prev,cur,index)=>{
      context.fillStyle = options.colorPool[index]
      let angle = calcPaintingData(cur,options);
      return prev + angle;
  },0);
  //绘制中空白色圆
  context.beginPath();
  context.fillStyle = 'white';
  context.arc(0,0,options.radius[0],0,2*Math.PI,false);
  context.fill();
}

/**
* 计算每个扇形所需要的绘图参数
*/
function calcPaintingData(data,options) {
   let scale = data.value / options.totalNum; 
   let angle = scale * 2 * Math.PI;
   let Rmin = options.radius[0];
   let Rmax = options.radius[1];
   let r = Math.sqrt(scale * (Rmax*Rmax - Rmin*Rmin) + Rmin*Rmin);
   data.r = r;
   //绘制扇形
   paintFan({
       r:r,
       angle:angle,
       data:data,
       options:options
   });
   return angle;//将角度值返回给外层函数以供累加
}

//绘制扇形
function paintFan(opt) {
   context.beginPath();
   context.lineTo(opt.r,0);
   context.arc(0,0,opt.r,0,opt.angle,false);
   context.lineTo(0,0);
   context.closePath();
   context.fill();
   context.rotate(opt.angle);
}

浏览器中可查看效果：

四. hover高亮的实现思路

绘图过程中，将每个扇区的绘图数据(半径，相对于圆心的起始转角，扇区角度)均挂载在绘图数据上。
在canvas标签上监听鼠标移动事件mousemove,并在回调函数中将鼠标移动事件event.clientX和event.clientY转换为相对于canvas坐标的数值(mouseX,mouseY)。
从圆心坐标(paintingCenter.x,paintingCenter.y)到(mouseX,mouseY)连接为向量，根据该向量的角度和模即可判断鼠标是否处于某个扇区之上。
如果处于扇区之上，则以过渡动画来绘制关键帧使得hover效果表现出来。先修改context.fillStyle颜色为对应扇区的高亮色，然后让外圆绘图半径以线性的方式逐帧增加至目标大小(例如10%),每一帧中使用canvas绘图上下文重新对绘图区域进行封闭画线，然后填充即可。
hover效果出现时绘制高亮色的绘图区域，hover效果消失时从外圆开始逐帧绘制白色外层扇区即可，最终再将数据扇区绘制为原色。