听说全部看懂Arrays.sort的都被面试官录取了

解析

源

码

我们来回顾一下Arrays.sort()的基础知识点：

1.可以直接排的基本数据类型是：int,long,short,char,byte,float,double,其余类型都归于对象类，Object[]；注意是没有boolean的

2.Arrays.sort()默认的是升序排序，降序排序可采用Collection.sort()匿名内部类。

上一篇我们讲解了Arrays.sort()的基本数据类型的排序，如果没有看到的可以看下面链接

深入理解Arrays.sort，怼哭面试官

之前我们在做最长公共前缀算法的时候，第二种方法提到过给字符串排个序，这样第一个和最后一个字符串就是前缀差别最大的两个，直接使用它们来做比较，直接获取最长公共前缀。如果没有印象的小伙伴可以参考下面文章：

算法养成记：最长公共前缀

Arrays.sort()主要就是分类两大部分，一部分是对基本数据类型的排序，另一部分就是对Object对象的排序，今天就来看看对Object的排序，也就是我们在做最长公共前缀时调用的方法。

首先我们可以看到，对于对象的排序，会有两个排序方法，MergeSort和TimSort，它们由“LegacyMergeSort.userRequested”这个参数决定。

MergeSort归并排序对已经反向排好序的输入时复杂度为O(n^2)，而TimSort就是针对这种情况，对MergeSort进行优化而产生的，平均复杂度为nO(log n),最好的情况为O(n)，最坏情况nO(log n)。并且TimSort是一种稳定性排序。思想是先对待排序列进行分区，然后再对分区进行合并，看起来和MergeSort步骤一样，但是其中有一些针对反向和大规模数据的优化处理。

LegacyMergeSort.userRequested的字面意思大概就是“用户请求传统归并排序”的意思，通过System.setProperty("java.util.Arrays.useLegacyMergeSort", "true")设置，

正如前文所提到的，TimSort由MergeSort优化而来，所以MergeSort会被弃用，如下图中，源码也提到了这一点

下面来看看MergeSort的实现

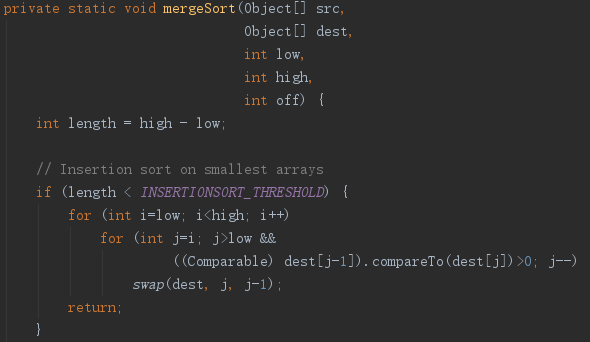
如上图，首先计算了长度，如果小于7，就用插入排序。INSERTIONSORT_THRESHOLD这个参数也会跟着MergeSort的弃用而移除。

如上图，如果大于7了，就开始递归的归并排序调用了。注意上图的>>>1，相当于除以2。就是拆成两部分，分别进行排序，之后再合并。

之后就是优化的一部分了， 即进行归并排序的两部分分别排序后， 前半部分的最大值小于后半部分的最小值，即已经是有序数组，就直接复制排序后的src 数组

之后就是合并排序后的数组，过程如下图所示。

接下来我们来看看ComparableTimSort；

imSort的重要思想是分区与合并
分区
分区的思想是扫描一次数组，把连续正序列（如果是升序排序，那么正序列就是升序序列），如果是反序列，把分区里的元素反转一下。

例如
1，2，3，6，4，5，8，6，4 划分分区结果为
[1,2,3,6],[4,5,8],[6,4]
然后反转反序列
[1,2,3,6],[4,5,8],[4,6]

合并
考虑一个极端的例子，比如分区的长度分别为 10000，10，1000，10，10，我们当然希望是先让10个10合并成20， 20和1000合并成1020如此下去， 如果从从左往右顺序合并的话，每次都用到10000这个数组和去小的数组合并，代价太大了。所以我们可以用一个策略来优化合并的顺序。

接下来看看ComparableTimSort的源码

如上图，首先判断一下长度，如果小于2，就直接返回；如果大于2，小于32，就执行叫“mini-TimSort
”的方法，它不包含合并操作，使用binarySort；

基本操作是：

1.从数组开始处找到一组连接升序或严格降序（找到后翻转）的数 

2.Binary Sort：使用二分查找的方法将后续的数插入之前的已排序数组，binarySort 对数组 a[lo:hi] 进行排序，并且a[lo:start] 是已经排好序的。算法的思路是对a[start:hi] 中的元素，每次使用binarySearch 为它在 a[lo:start] 中找到相应位置，并插入。

下面我们来看看countRunAndMakeAscending函数是如何实现查找严格升序或者严格降序的

如上图，

countRunAndMakeAscending方法接收的参数有三个，待查找的数组，起始下标，终点下标。

基本思想是：判断第二个数和第一个数的大小来确定是升序还是降序，

1.若第二个数小于第一个数，则为降序，然后在while循环中，若后后面的数依旧小于前面的数，则runHi++计数，直到不满足降序；然后调用reverseRange进行反转，变成升序。

2.若第二个数大于第一个数，则为升序，然后在while循环中，若后面的数依旧大于前面的数，则runHi++计数，直到不满足升序。

3.返回runHi - lo也就是严格满足升序或者降序的个数。且这个严格序列是从第一个开始的。最后都是严格的升序序列。

所以！

在执行binarySort方法的时候只需要将lo + initRunLen后的数依此插入前面的升序序列中即可

如上图，如若待排序数组若大于阈值MIN_MERGE，则直接进行排序，我们一步一步讲。

1.如果 n < MIN_MERGE, 直接返回 n。（太小了，不值得做复杂的操作）；   

2.如果 n 正好是2的幂，返回 n / 2； 

3.其它情况下 返回一个数 k，满足 MIN_MERGE/2 <= k <= MIN_MERGE,  这样结果就能保证 n/k 非常接近但小于一个2的幂。这个数字实际上是一种空间与时间的优化。

接下来看看do-while干了什么

首先执行了countRunAndMakeAscending(a, lo, hi)上面已经提到过了，不用赘述；

找到a中从第一个数开始的严格升序，如果是降序，则反转成升序序列。若找到的升序序列的个数runLen小于minRun，由上面可知，minRun的范围在:[16,32]，force取nRemaining和minRun中较小的那个。然后利用折半查找binarySort进行排序

a[lo,runLen]是有序的，将其入栈ts.pushRun(lo, runLen);目的是为后续merge各区块作准备：记录当前已排序的各区块的大小

lo += runLen;

nRemaining -= runLen;

这里实际就是剔除了有序的a[lo,runLen]段，然后将剩下的重新循环dowhile的步骤，直到全部有序。

是不是一脸懵？

懵就对了，对看两遍就懂了。