1、数独问题
你一定听说过“数独”游戏。
如【图1.png】,玩家需要根据9×9盘面上的已知数字,推理出所有剩余空格的数字,并满足每一行、每一列、每一个同色九宫内的数字均含1-9,不重复。

数独的答案都是唯一的,所以,多个解也称为无解。
本图的数字据说是芬兰数学家花了3个月的时间设计出来的较难的题目。但对会使用计算机编程的你来说,恐怕易如反掌了。
本题的要求就是输入数独题目,程序输出数独的唯一解。我们保证所有已知数据的格式都是合法的,并且题目有唯一的解。
格式要求:
输入9行,每行9个数字,0代表未知,其它数字为已知。
输出9行,每行9个数字表示数独的解。
例如:
输入(即图中题目):
005300000
800000020
070010500
400005300
010070006
003200080
060500009
004000030
000009700
程序应该输出:
145327698
839654127
672918543
496185372
218473956
753296481
367542819
984761235
521839764
再例如,输入:
800000000
003600000
070090200
050007000
000045700
000100030
001000068
008500010
090000400
程序应该输出:
812753649
943682175
675491283
154237896
369845721
287169534
521974368
438526917
796318452
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 2000ms
【分析】:回溯法每个位置进行试探。判断能否装入的条件:在同行同列中不能出现相同的数字,并且在一个边长为3的正方形中,不能有重复的数字出现。
/**用数组来标记每行每列已经出现的数字**/
rvis[x][value] = 1; //表示第x行数字为value已经存在
rvis[y][value] = 1; //表示第y列数字为value已经存在
//对于正方形区域
int check(int x,int y,int value)
{
int m=x/3*3,n=y/3*3;
for(int i=m; i<m+3; i++)
for(int j=n; j<n+3; j++)
if(a[i][j]==value)
return 0;
return 1;
}
完整的代码:
//数独
#include<iostream>
#include<string.h>
using namespace std;
int a[10][10];
int rvis[15][15];
int cvis[15][15];
int check(int x,int y,int value)//检查方形中value是否出现
{
int m=x/3*3,n=y/3*3;
for(int i=m; i<m+3; i++)
for(int j=n; j<n+3; j++)
if(a[i][j]==value)
return 0;
return 1;
}
void dfs(int x,int y)
{
if(x > 8)
{
for(int i=0; i<9; i++)
{
for(int j=0; j<9; j++)
cout<<a[i][j];
cout<<endl;
}
return;
}
if(a[x][y] == 0)
{
for(int i=1; i<10; i++)
{
if(!rvis[x][i] && !cvis[y][i] && check(x,y,i))//可以放入
{
rvis[x][i] = 1;
cvis[y][i] = 1;
a[x][y] = i;
if(y==8)
dfs(x+1,0);
else
dfs(x,y+1);
a[x][y]=0;//回溯
rvis[x][i] = 0;
cvis[y][i] = 0;
}
}
}
else
{
if(y==8)
dfs(x+1,0);
else
dfs(x,y+1);
}
}
int main()
{
memset(rvis,0,sizeof(rvis));//赋值
memset(cvis,0,sizeof(cvis));
char str[9][9];//注意输入的是字符串
for(int i=0; i<9; i++)
gets(str[i]);
for(int i=0; i<9; i++)
{
for(int j=0; j<9; j++)
{
a[i][j] = str[i][j]-'0';//将输入的字符串转换成数字
if(a[i][j] != 0)
{
rvis[i][a[i][j]] = 1;
cvis[j][a[i][j]] = 1;
}
}
}
dfs(0,0);//进行深度优先搜索
return 0;
}
2、7对数字
今有7对数字:两个1,两个2,两个3,…两个7,把它们排成一行。
要求,两个1间有1个其它数字,两个2间有2个其它数字,以此类推,两个7之间有7个其它数字。如下就是一个符合要求的排列:
17126425374635
当然,如果把它倒过来,也是符合要求的。
请你找出另一种符合要求的排列法,并且这个排列法是以74开头的。
注意:只填写这个14位的整数,不能填写任何多余的内容,比如说明注释等。
【分析】:直接DFS
#include<iostream>
#include<string.h>
using namespace std;
int a[15];
int vis[15];
void dfs(int n)
{
if(n==4 || n==7)
{
dfs(n+1);
return;
}
if(n>7)
{
for(int i=0;i<14; i++)
cout<<a[i];
cout<<endl;
return;
}
for(int i=2; i<13-n; i++)
{
if(!vis[i] && !vis[i+n+1])
{
a[i]=a[i+n+1]=n;
vis[i]=vis[i+n+1]=1;
dfs(n+1);
a[i]=a[i+n+1]=0;
vis[i]=vis[i+n+1]=0;
}
}
}
int main()
{
memset(vis,0,sizeof(vis));
vis[0]=vis[8]=1;
vis[1]=vis[6]=1;
a[0]=a[0+7+1]=7;
a[1]=a[1+4+1]=4;
dfs(1);
return 0;
}
3、九数组分数
1,2,3…9 这九个数字组成一个分数,其值恰好为1/3,如何组法?
下面的程序实现了该功能,请填写划线部分缺失的代码。
#include <stdio.h>
void test(int x[])
{
int a = x[0]*1000 + x[1]*100 + x[2]*10 + x[3];
int b = x[4]*10000 + x[5]*1000 + x[6]*100 + x[7]*10 + x[8];
if(a*3==b) printf("%d / %d\n", a, b);
}
void f(int x[], int k)
{
int i,t;
if(k>=9){
test(x);
return;
}
for(i=k; i<9; i++){
{t=x[k]; x[k]=x[i]; x[i]=t;}
f(x,k+1);
_____________________________________________ // 填空处
}
}
int main()
{
int x[] = {1,2,3,4,5,6,7,8,9};
f(x,0);
return 0;
}
//DFS的回溯
{t=x[k]; x[k]=x[i]; x[i]=t;}
4、牌型种数
小明被劫持到X赌城,被迫与其他3人玩牌。
一副扑克牌(去掉大小王牌,共52张),均匀发给4个人,每个人13张。
这时,小明脑子里突然冒出一个问题:
如果不考虑花色,只考虑点数,也不考虑自己得到的牌的先后顺序,自己手里能拿到的初始牌型组合一共有多少种呢?
#include<iostream>
using namespace std;
int ans=0;
void dfs(int n,int sum)
{
if(n > 13)
{
if(sum == 13)
ans++;
return;
}
if(sum > 13)
return;
for(int i=0; i<5; i++)//对于 n 个点数的牌,拿几张
{
sum += i;
dfs(n+1,sum);
sum -= i;
}
}
int main()
{
dfs(1,0);
cout<<ans<<endl;
return 0;
}
5、垒骰子
赌圣atm晚年迷恋上了垒骰子,就是把骰子一个垒在另一个上边,不能歪歪扭扭,要垒成方柱体。
经过长期观察,atm 发现了稳定骰子的奥秘:有些数字的面贴着会互相排斥!
我们先来规范一下骰子:1 的对面是 4,2 的对面是 5,3 的对面是 6。
假设有 m 组互斥现象,每组中的那两个数字的面紧贴在一起,骰子就不能稳定的垒起来。
atm想计算一下有多少种不同的可能的垒骰子方式。
两种垒骰子方式相同,当且仅当这两种方式中对应高度的骰子的对应数字的朝向都相同。
由于方案数可能过多,请输出模 10^9 + 7 的结果。
不要小看了 atm 的骰子数量哦~
「输入格式」
第一行两个整数 n m
n表示骰子数目
接下来 m 行,每行两个整数 a b ,表示 a 和 b 数字不能紧贴在一起。
「输出格式」
一行一个数,表示答案模 10^9 + 7 的结果。
「样例输入」
2 1
1 2
「样例输出」
544
「数据范围」
对于 30% 的数据:n <= 5
对于 60% 的数据:n <= 100
对于 100% 的数据:0 < n <= 10^9, m <= 36
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 2000ms
#include<iostream>
using namespace std;
#define mod 1000000007
int map[]={0,4,5,6,1,2,3};//存放每个面的对应面
int rule[7]={0};//存放不能相对的面
int m,n;
long long ans=0;
void dfs(int height,int up)
{
if(height > n)
{
ans=(ans+1)%mod;
return;
}
for(int i=1; i<=6; i++)
{
if(rule[up] != i)
dfs(height+1,map[i]);
}
}
int main()
{
cin>>n>>m;
for(int i=0; i<m; i++)
{
int a,b;
cin>>a>>b;
rule[a]=b;
rule[b]=a;
}
dfs(1,0);
for(int i=0; i<n; i++)//对于每一层的骰子,都可以进行旋转,四个方向
ans = ans%mod*4;
cout<<ans<<endl;
return 0;
}
6、方格填数
在2行5列的格子中填入1到10的数字。
要求:
相邻的格子中的数,右边的大于左边的,下边的大于上边的。
如【图1.png】所示的2种,就是合格的填法。
请你计算一共有多少种可能的方案。

#include<iostream>
using namespace std;
int map[2][5];
int vis[10]={0};
int ans=0;
void dfs(int x,int y)
{
if(x==1 && y==4)
{
ans++;
return;
}
for(int i=2; i<=9; i++)
{
if(vis[i]) continue;
if(x==0)
{
if(map[x][y-1] < i)//在第一行时,只比较右边比左边大
{
map[x][y]=i;
vis[i]=1;
if(y==4)
dfs(x+1,0);
else
dfs(x,y+1);
vis[i]=0;
}
}
else
{
if(map[x-1][y] < i)//比较下边比上边大
{
if(y>0 && map[x][y-1] > i)//比较右边比左边大
continue;
map[x][y]=i;
vis[i]=1;
if(y==4)
dfs(x+1,0);
else
dfs(x,y+1);
vis[i]=0;
}
}
}
}
int main()
{
map[0][0]=1;
map[1][4]=10;
dfs(0,1);
cout<<ans<<endl;
return 0;
}
7、四阶幻方
把1~16的数字填入4x4的方格中,使得行、列以及两个对角线的和都相等,满足这样的特征时称为:四阶幻方。
四阶幻方可能有很多方案。如果固定左上角为1,请计算一共有多少种方案。
比如:
1 2 15 16
12 14 3 5
13 7 10 4
8 11 6 9
以及:
1 12 13 8
2 14 7 11
15 3 10 6
16 5 4 9
就可以算为两种不同的方案。
#include<iostream>
#include<string.h>
using namespace std;
int map[4][4];
int vis[17]={0};
int ans=0;
int check()
{
for(int i=0; i<4; i++)
{
int sum=0;
for(int j=0; j<4; j++)
{
sum+=map[j][i];
}
if(sum != 34)
return 0;
}
int a=map[0][0]+map[1][1]+map[2][2]+map[3][3];
int b=map[0][3]+map[1][2]+map[2][1]+map[3][0];
if(a!=34 || b!=34)
return 0;
return 1;
}
void dfs(int x,int y,int sum)
{
if(x>3)
{
if(check())
ans++;
return;
}
for(int i=2; i<=16; i++)
{
if(!vis[i])
{
if(sum+i > 34)//剪枝
break;
map[x][y]=i;
vis[i]=1;
if(y==3){
if(sum+i == 34)//判断一行总和值
dfs(x+1,0,0);
}
else
dfs(x,y+1,sum+i);
vis[i]=0;
}
}
}
int main()
{
memset(map,0,sizeof(map));
map[0][0]=1;
vis[1]=1;
dfs(0,1,1);
cout<<ans<<endl;
return 0;
}
8、方格填数
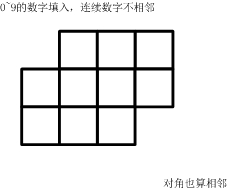
如下的10个格子
±-±-±-+
| | | |
±-±-±-±-+
| | | | |
±-±-±-±-+
| | | |
±-±-±-+
(如果显示有问题,也可以参看【图1.jpg】)
填入0~9的数字。要求:连续的两个数字不能相邻。
(左右、上下、对角都算相邻)
一共有多少种可能的填数方案?
#include<iostream>
#include<math.h>
using namespace std;
int map[4][5]={-2};
int vis[10]={0};
int ans=0;
void dfs(int x,int y)
{
if(x==3 && y==3)
{
ans++;
return;
}
for(int i=0; i<=9; i++)
{
if(vis[i]) continue;
if(x==1)
{
if(abs(map[x][y-1]-i) == 1)
continue;
}
else
{
int a = abs(map[x-1][y]-i);
int b = abs(map[x-1][y-1]-i);
int c = abs(map[x][y-1]-i);
int d = abs(map[x-1][y+1]-i);
if(a==1 || b==1 || c==1 ||d==1)
continue;
}
vis[i]=1;
map[x][y]=i;
if(y==4)
dfs(x+1,1);
else
dfs(x,y+1);
vis[i]=0;
}
}
int main()
{
dfs(1,2);
cout<<ans<<endl;
return 0;
}
9、寒假作业
每个方块代表1~13中的某一个数字,但不能重复。
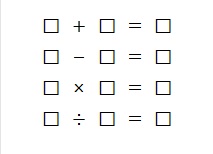
比如:
6 + 7 = 13
9 - 8 = 1
3 * 4 = 12
10 / 2 = 5
以及:
7 + 6 = 13
9 - 8 = 1
3 * 4 = 12
10 / 2 = 5
就算两种解法。(加法,乘法交换律后算不同的方案)
你一共找到了多少种方案?
#include<iostream>
using namespace std;
int vis[14]={0};
int a[12]={0};
int ans=0;
void dfs(int n)
{
if(n==3)
{
if(a[0]+a[1] != a[2])
return;
}
if(n==6)
{
if(a[3]-a[4] != a[5])
return;
}
if(n==9)
{
if(a[6]*a[7] != a[8])
return;
}
if(n>11)
{
if(a[9]/a[10] == a[11])
ans++;
return;
}
for(int i=1; i<=13; i++)
{
if(!vis[i])
{
vis[i]=1;
a[n]=i;
dfs(n+1);
vis[i]=0;
}
}
}
int main()
{
dfs(0);
cout<<ans<<endl;
return 0;
}
10、密码脱落
X星球的考古学家发现了一批古代留下来的密码。
这些密码是由A、B、C、D 四种植物的种子串成的序列。
仔细分析发现,这些密码串当初应该是前后对称的(也就是我们说的镜像串)。
由于年代久远,其中许多种子脱落了,因而可能会失去镜像的特征。
你的任务是:
给定一个现在看到的密码串,计算一下从当初的状态,它要至少脱落多少个种子,才可能会变成现在的样子。
输入一行,表示现在看到的密码串(长度不大于1000)
要求输出一个正整数,表示至少脱落了多少个种子。
例如,输入:
ABCBA
则程序应该输出:
0
再例如,输入:
ABDCDCBABC
则程序应该输出:
3
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 1000ms
#include<iostream>
using namespace std;
int dfs(char* start,char* end)
{
if(start>=end)
return 0;
else
{
if(*start == *end)
return dfs(start+1,end-1);
else
{
return min(1+dfs(start,end-1),1+dfs(start+1,end));
}
}
}
int main()
{
string str;
cin>>str;
char *p1,*p2;
p1 = &str[0];
p2 = &str[str.length()-1];
int ans=dfs(p1,p2);
cout<<ans<<endl;
}
11.随意组合
小明被绑架到X星球的巫师W那里。
其时,W正在玩弄两组数据 (2 3 5 8) 和 (1 4 6 7)
他命令小明从一组数据中分别取数与另一组中的数配对,共配成4对(组中的每个数必被用到)。
小明的配法是:{(8,7),(5,6),(3,4),(2,1)}
巫师凝视片刻,突然说这个配法太棒了!
因为:
每个配对中的数字组成两位数,求平方和,无论正倒,居然相等:
87^2 + 56^2 + 34^2 + 21^2 = 12302
78^2 + 65^2 + 43^2 + 12^2 = 12302
小明想了想说:“这有什么奇怪呢,我们地球人都知道,随便配配也可以啊!”
{(8,6),(5,4),(3,1),(2,7)}
86^2 + 54^2 + 31^2 + 27^2 = 12002
68^2 + 45^2 + 13^2 + 72^2 = 12002
巫师顿时凌乱了。。。。。
请你计算一下,包括上边给出的两种配法,巫师的两组数据一共有多少种配对方案具有该特征。
配对方案计数时,不考虑配对的出现次序。
就是说:
{(8,7),(5,6),(3,4),(2,1)}
与
{(5,6),(8,7),(3,4),(2,1)}
是同一种方案。
#include<iostream>
using namespace std;
#include<math.h>
int vis[4]={0};
int a[]={2,3,5,8};
int b[]={1,4,6,7};
int c[4]={0};
int ans=0;
int check()
{
int sum1=0,sum2=0;
for(int i=0; i<4; i++)
{
sum1+=pow(a[i]*10+c[i],2);
sum2+=pow(a[i]+c[i]*10,2);
}
if(sum1==sum2)
return 1;
else
return 0;
}
void dfs(int n)
{
if(n>3)
{
if(check())
ans++;
return;
}
for(int i=0; i<4; i++)
{
if(!vis[i])
{
vis[i]=1;
c[n]=b[i];
dfs(n+1);
vis[i]=0;
c[n]=0;
}
}
}
int main()
{
dfs(0);
cout<<ans<<endl;
return 0;
}























 1230
1230

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








