花书+吴恩达深度学习（四）多分类 softmax

本文链接：https://blog.youkuaiyun.com/zhq9695/article/details/84726239

本文深入探讨了神经网络中常见的激活函数，包括二分类问题中的sigmoid函数和多分类问题中的softmax函数。详细解析了这两种函数的工作原理，以及如何在梯度下降过程中进行推导。适合对深度学习和神经网络感兴趣的读者。

如果这篇文章对你有一点小小的帮助，请给个关注，点个赞喔~我会非常开心的~

花书+吴恩达深度学习（一）前馈神经网络（多层感知机 MLP）

花书+吴恩达深度学习（二）非线性激活函数（ReLU, maxout, sigmoid, tanh）

花书+吴恩达深度学习（三）反向传播算法 Back Propagation

花书+吴恩达深度学习（四）多分类 softmax

0. 前言

在神经网络的输出单元，通常采用与隐藏单元不同的激活函数。

二分类中，通常采用 sigmoid 函数：

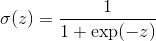
$\sigma(z)=\frac{1}{1+\exp(-z)}$

多分类中，通常采用 softmax 函数：

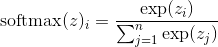
$\textup{softmax}(z)_i=\frac{\exp(z_i)}{\sum_{j=1}^n\exp(z_j)}$

1. 二分类 sigmoid

在二分类中，最后一层网络仅有一个单元：

$\begin{align*} & Z^{[L]}=W^{[L]}A^{[L-1]}+B^{[L]} \\ & A^{[L]}=\sigma(Z^{[L]}) \end{align*}$

因为 sigmoid 的值域为 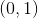(0,1) ，所以最后一个单元表示输出正类（反类）的概率。

在使用梯度下降时：

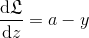
$\frac{\mathrm{d} \mathfrak{L}}{\mathrm{d} z}=a-y$

详细的推导可以移步我的博客。

2. 多分类 softmax

在多分类中，最后一层网络有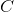个单元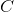（表示类别数量）：

$\begin{align*} & Z^{[L]}=W^{[L]}A^{[L-1]}+B^{[L]} \\ & A^{[L]}_i=\frac{\exp(Z^{[L]}_i)}{\sum_{j=1}^C\exp(Z^{[L]}_j)} \end{align*}$

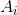A_i 为最后一层网络第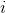个单元的输出，这使得最后一层网络总和为。

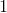数值最大的单元，为最终类别，我们将类别向量化：

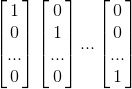
$\begin{bmatrix} 1\\ 0\\ ...\\ 0 \end{bmatrix} \begin{bmatrix} 0\\ 1\\ ...\\ 0 \end{bmatrix} ... \begin{bmatrix} 0\\ 0\\ ...\\ 1 \end{bmatrix}$

3. 多分类 softmax 梯度下降推导

在使用梯度下降时，与 sigmoid 相同，可以看作是 sigmoid 的多分类版本：

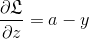
$\frac{\partial \mathfrak{L}}{\partial z}=a-y$

使用对数最大似然定义代价函数：

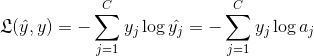
$\mathfrak{L}(\hat{y},y)=-\sum_{j=1}^Cy_j\log \hat{y_j}=-\sum_{j=1}^Cy_j\log a_j$

根据链式求导法则，梯度下降表示为：

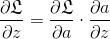
$\frac{\partial \mathfrak{L}}{\partial z}=\frac{\partial \mathfrak{L}}{\partial a}\cdot \frac{\partial a}{\partial z}$

第一项的求导：

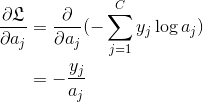
$\begin{align*} \frac{\partial \mathfrak{L}}{\partial a_j} &= \frac{\partial }{\partial a_j}(-\sum_{j=1}^Cy_j\log a_j) \\ &= -\frac{y_j}{a_j} \end{align*}$

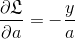
$\frac{\partial \mathfrak{L}}{\partial a}=-\frac{y}{a}$

第一项的导数是一个 $1\times C$ 的向量：

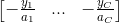
$\begin{bmatrix} -\frac{y_1}{a_1} &... & -\frac{y_C}{a_C} \end{bmatrix}$

第二项的求导：

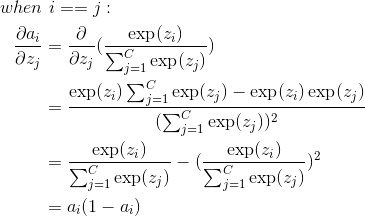
$\begin{align*} when & \ i==j: \\ \frac{\partial a_i}{\partial z_j}&= \frac{\partial}{\partial z_j}(\frac{\exp(z_i)}{\sum_{j=1}^C\exp(z_j)}) \\ &= \frac{\exp(z_i)\sum_{j=1}^C\exp(z_j)-\exp(z_i)\exp(z_j)}{(\sum_{j=1}^C\exp(z_j))^2} \\ &= \frac{\exp(z_i)}{\sum_{j=1}^C\exp(z_j)}-(\frac{\exp(z_i)}{\sum_{j=1}^C\exp(z_j)})^2 \\ &= a_i(1-a_i) \end{align*}$

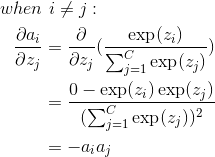
$\begin{align*} when&\ i\neq j: \\ \frac{\partial a_i}{\partial z_j}&= \frac{\partial}{\partial z_j}(\frac{\exp(z_i)}{\sum_{j=1}^C\exp(z_j)}) \\ &= \frac{0-\exp(z_i)\exp(z_j)}{(\sum_{j=1}^C\exp(z_j))^2} \\ &= -a_ia_j \end{align*}$

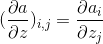
$(\frac{\partial a}{\partial z})_{i,j}=\frac{\partial a_i}{\partial z_j}$

第二项的导数是一个 $C\times C$ 的 Jacobian 矩阵：

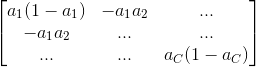
$\begin{bmatrix} a_1(1-a_1) & -a_1a_2 &... \\ -a_1a_2 &... &... \\ ... & ... & a_C(1-a_C) \end{bmatrix}$

综上所述：

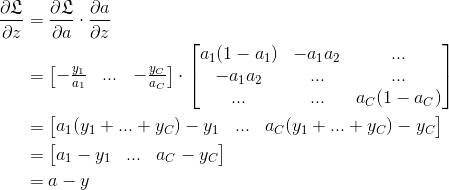
$\begin{align*} \frac{\partial \mathfrak{L}}{\partial z}&=\frac{\partial \mathfrak{L}}{\partial a}\cdot \frac{\partial a}{\partial z}\\ &=\begin{bmatrix} -\frac{y_1}{a_1} &... & -\frac{y_C}{a_C} \end{bmatrix}\cdot \begin{bmatrix} a_1(1-a_1) & -a_1a_2 &... \\ -a_1a_2 &... &... \\ ... & ... & a_C(1-a_C) \end{bmatrix}\\ &= \begin{bmatrix} a_1(y_1+...+y_C)-y_1 &... & a_C(y_1+...+y_C)-y_C \end{bmatrix}\\ &= \begin{bmatrix} a_1-y_1 &... &a_C-y_C \end{bmatrix}\\ &= a-y \end{align*}$