Python实战：递归

Python递归是一种非常重要的算法思想，它可以使得我们在处理复杂问题时更加高效，让我们来看一个简单的例子。

 Python递归是指在函数定义中调用自身函数的过程。递归是一种常用的算法，可以解决许多复杂的问题。本文将介绍Python递归的概念、原理、实现方法和应用场景。

1. 递归的概念

递归是指在函数的定义中调用函数自身的过程。递归函数通常包含两个部分：基本情况和递归情况。基本情况是指函数的输入参数满足某个条件时，函数不再调用自身，直接返回结果。递归情况是指函数的输入参数不满足基本情况时，函数调用自身，并将参数修改为某个值。

2. 递归的原理

递归的原理是将一个大问题分解成许多小问题，并通过递归函数依次解决这些小问题，最终得到大问题的解。递归函数的调用过程可以用栈来模拟。每次递归调用时，将函数的参数和返回地址压入栈中，递归函数返回时，从栈中弹出参数和返回地址，继续执行下一条指令。

3. 递归的实现方法

Python递归的实现方法是在函数定义中调用自身函数，并在函数内部判断是否满足基本情况。如果满足基本情况，直接返回结果；否则，调用自身函数，并将参数修改为某个值。

下面是一个计算阶乘的递归函数的示例代码：

```python
def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)
```

在上面的代码中，我们定义了一个名为factorial的函数，它接受一个整数n作为参数。如果n等于0，函数直接返回1；否则，函数调用自身，并将参数修改为n-1。最终，函数返回n的阶乘。

4. 递归的应用场景

递归是一种常用的算法，可以解决许多复杂的问题。递归的应用场景包括：

- 数学问题，如计算阶乘、计算斐波那契数列等；
- 数据结构问题，如遍历树、求解迷宫等；
- 编程问题，如实现快速排序、实现分治算法等。

5. 案例

假设我们要计算一个数的阶乘，阶乘的定义是：n! = n * (n-1) * (n-2) * ... * 2 * 1。

我们可以使用循环来实现这个功能，但是这种方法有一个问题，就是对于大数计算，会涉及到大量的乘法运算，导致计算时间过长。这时候，递归就可以帮助我们解决这个问题。

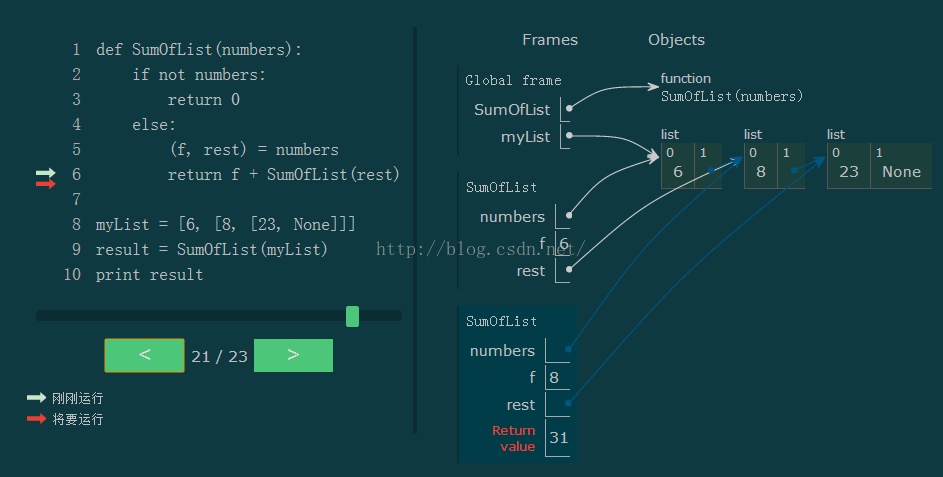
递归的思想是将一个问题分解成更小的子问题来解决。对于阶乘计算，我们可以将n!分解成(n-1)!，以此类推，直到n=1时，n!=1。

下面是一个用Python实现阶乘递归的代码：

def factorial(n):
    if n == 1:
        return 1
    else:
        return n * factorial(n-1)

在这个代码中，我们定义了一个函数factorial，它接收一个整数n作为参数。如果n等于1，那么我们返回1，否则我们返回n * factorial(n-1)。这个函数的意思是，如果n等于1，那么它的阶乘就是1，否则它的阶乘就是n乘以(n-1)的阶乘。

我们可以使用下面的代码来测试这个函数：

print(factorial(5)) # 输出 120

这个代码的输出结果是120，这是因为5的阶乘是120。

递归虽然可以帮助我们解决一些复杂的问题，但是它也有一些缺点。递归的调用过程会占用大量的栈空间，如果递归的深度过大，就会导致栈溢出的问题。因此，在使用递归时，我们需要注意控制递归的深度。

运行环境：Windows Shell Python 3.4  IDE（注意：与2.*版本的Python在语法上是有差别的）

总结

Python递归是指在函数定义中调用自身函数的过程。递归函数通常包含两个部分：基本情况和递归情况。递归的原理是将一个大问题分解成许多小问题，并通过递归函数依次解决这些小问题，最终得到大问题的解。Python递归的实现方法是在函数定义中调用自身函数，并在函数内部判断是否满足基本情况。递归的应用场景包括数学问题、数据结构问题和编程问题等。

---

更多资料 · 微信公众号搜索【CTO Plus】关注后，获取更多，我们一起学习交流。

或者点击下方链接

---

关于Articulate“做一个知识和技术的搬运工。做一个终身学习的爱好者。做一个有深度和广度的技术圈。”一直以来都想把专业领域的技https://mp.weixin.qq.com/s/0yqGBPbOI6QxHqK17WxU8Q