leetcode：54. 螺旋矩阵

题目来源

• leetcode：54. 螺旋矩阵

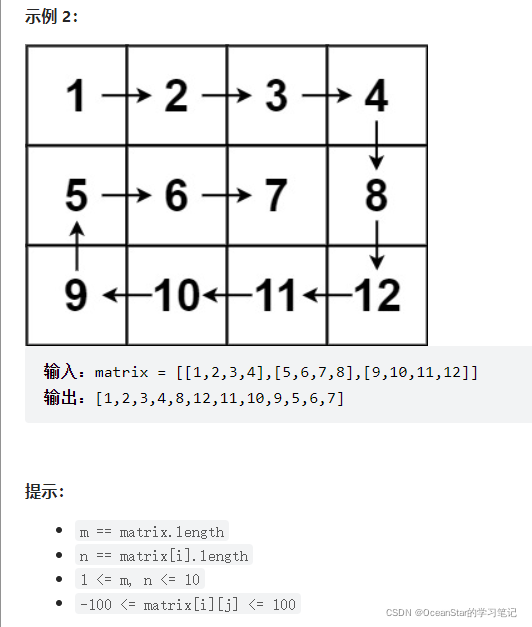
题目描述

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {

    }
};

题目解析

模拟（设定边界）

思路

• 首先设定上下左右边界
• 其次向右启动到最右，此时第一行因为已经使用过了，可以将其从图中删除，体现在代码中就是重新定义上边界
• 判断如果重新定义后，上下边界交错，表示螺旋矩阵遍历结束，跳出循环，返回答案
• 若上下边界不交错，则遍历还未结束，接着向下向左向上移动，操作过程与第一，二步同理
• 不断循环以上步骤，直到某两条边界交错，跳出循环，返回答案

实现

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        vector <int> ans;
        if(matrix.empty()) return ans; //若数组为空，直接返回答案
        int u = 0; //赋值上下左右边界
        int d = matrix.size() - 1;
        int l = 0;
        int r = matrix[0].size() - 1;
        while(true)
        {
            for(int i = l; i <= r; ++i) ans.push_back(matrix[u][i]); //向右移动直到最右
            if(++ u > d) break; //重新设定上边界，若上边界大于下边界，则遍历遍历完成，下同
            for(int i = u; i <= d; ++i) ans.push_back(matrix[i][r]); //向下
            if(-- r < l) break; //重新设定有边界
            for(int i = r; i >= l; --i) ans.push_back(matrix[d][i]); //向左
            if(-- d < u) break; //重新设定下边界
            for(int i = d; i >= u; --i) ans.push_back(matrix[i][l]); //向上
            if(++ l > r) break; //重新设定左边界
        }
        return ans;
    }
};

按照形状进行模拟

我们可以按[圈]进行划分打印。

• 使用[左上角]（x1, y1）和[右下角]（x2，y2）来确定某个[圈]，进行打印。
• 完成后，令[左上角]&&[右下角]往里收，分别得到（x1+1， y1 + 1）和 (x2 - 1, y2 - 1)，执行相同的打印规则

class Solution {
    void helper(vector<vector<int>>& matrix, std::vector<int> &ans, int x1, int y1, int x2, int y2){
        if (x2 < x1 || y2 < y1) return;

        // 只有一行时，按「行」遍历
        if(x1 == x2){
            for (int i = y1; i <= y2; ++i) ans.emplace_back(matrix[x1][i]);
            return;
        }

        // 只有一列时，按「列」遍历
        if(y1 == y2){
            for (int i = x1; i <= x2; ++i) ans.emplace_back(matrix[i][y1]);
            return;
        }

        // 遍历当前「圈」
        for (int i = y1; i < y2; ++i) ans.emplace_back(matrix[x1][i]);
        for (int i = x1; i < x2; ++i) ans.emplace_back(matrix[i][y2]);
        for (int i = y2; i > y1; --i) ans.emplace_back(matrix[x2][i]);
        for (int j = x2; j > x1; --j) ans.emplace_back(matrix[j][y1]);

        helper(matrix, ans, x1 + 1, y1 + 1, x2 - 1, y2 - 1);
    }
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        std::vector<int> ans;
        helper(matrix, ans, 0, 0, matrix.size() - 1, matrix[0].size() - 1);
        return ans;
    }
};

按照「方向」进行模拟

这种解法更为简洁。
因为每一圈的打印输出都是按照特定的「四个方向」进行的。
而触发方向转换的时机：

• 下一步发生位置溢出
• 回到了本圈的起点

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        std::vector<std::vector<int>> dir{{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
        std::vector<int> ans;
        int x = 0, y = 0, d = 0, tx, ty;
        int m = matrix.size(), n = matrix[0].size();
        int total = m * n;
        while (total != 0){
            ans.emplace_back(matrix[x][y]);
            matrix[x][y] = 101;
            --total;
            tx = x + dir[d][0], ty = y + dir[d][1];
            if(tx == -1 || ty == -1 || tx == m || ty == n || matrix[tx][ty] == 101){
                d = (d + 1) % 4;
                tx = x + dir[d][0], ty = y + dir[d][1];
            }
            x = tx, y = ty;
        }
        return ans;
    }
};

类似题目

思路
54. 顺时针螺旋矩阵
59. 生成螺旋矩阵