一、神经网络的介绍
1.1 概念
神经网络的出现就是为了解决设定权重的工作(即确定合适的、能符合预期的输入与输出的权重,现在还是由人工进行的),具体地讲,神经网络的一个重要性质是它可以自动地从数据中学习到合适的权重参数。
用图来表示神经网络,把最左边的一列称为输入层,最右边的一列称为输出层,中间的一列称为中间层。中间层有时也称为隐藏层。“隐藏”一词的意思是,隐藏层的神经元(和输入层、输出层不同)肉眼看不见。另外,把输入层到输出层依次称为第0 层、第1 层、第2 层(层号之所以从0 开始,是为了方便后面基于Python 进行实现)。
图中,第0 层对应输入层,第1 层对应中间层,第2 层对应输出层。

1.2 神经网络的内积


使用np.dot(多维数组的点积),可以一次性计算出Y 的结果。这意味着,即便Y 的元素个数为100或1000,也可以通过一次运算就计算出结果!如果不使用np.dot,就必须单独计算Y 的每一个元素(或者说必须使用for语句),非常麻烦。因此,通过矩阵的乘积一次性完成计算的技巧,在实现的层面上可以说是非常重要的。
二、激活函数
2.1激活函数的概念
激活函数是连接感知机和神经网络的桥梁。

h(x)函数会将输入信号的总和转换为输出信号,这种函数一般称为 激活函数(activation function)。如“激活”一词所示,激活函数的作用在于决定如何来激活输入信号的总和。
现在来进一步改写,先计算输入信号的加权总和,然后用激活函数转换这一总和。


2.2常见的激活函数
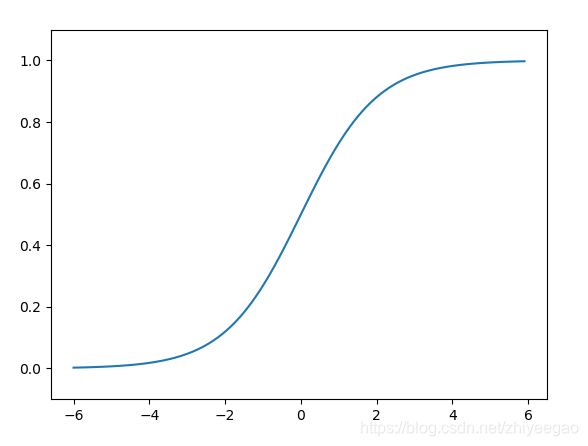
2.2.1 sigmoid 函数

神经网络中用sigmoid 函数作为激活函数,进行信号的换,转换后的信号被传送给下一个神经元。
def sigmoid(x):
return 1/(1+np.exp(-x))
注:之所以sigmoid 函数的实现能支持NumPy数组,秘密就在于NumPy的广播功能。根据NumPy 的广播功能,如果在标量和NumPy数组之间进行运算,则标量会和NumPy数组的各个元素进行运算。
2.2.2 阶跃函数
当输入超过0 时,输出1,否则输出0。

def step_function(x):
y = x>0
return y.astype(np.int)
2.2.3 sigmoid函数和阶跃函数的比较

首先注意到的是“平滑性”的不同。sigmoid 函数是一条平滑的曲线,输出随着输入发生连续性的变化。而阶跃函数以0 为界,输发生急剧性的变化。sigmoid 函数的平滑性对神经网络的学习具有重要意义。另一个不同点是,相对于阶跃函数只能返回0 或1,sigmoid 函数可以返回0.731 . . .、0.880 . . . 等实数。也就是说,感知机中神经元之间流动的是0 或1 的二元信号,而神经网络中流动的是连续的实数值信号。
阶跃函数和sigmoid函数虽然在平滑性上有差异,但是如果从宏观视角看,可以发现它们具有相似的形状。实际上,两者的结构均是“输入小时,输出接近0(为0);随着输入增大,输出向1 靠近(变成1)”。也就是说,当输入信号为重要信息时,阶跃函数和sigmoid函数都会输出较大的值;当输入信号为不重要的信息时,两者都输出较小的值。还有一个共同点是,不管输入信号有多小,或者有多大,输出信号的值都在0 到1 之间。
阶跃函数和sigmoid 函数还有其他共同点,就是两者均为非线性函数。
注: 神经网络的激活函数必须使用非线性函数。换句话说,激活函数不能使用线性函数。因为使用线性函数的话,加深神经网络的层数就没有意义了。
证明:考虑把线性函数h(x) = cx 作为激活函数,把y(x) = h(h(h(x))) 的运算对应3层神经网络。这个运算会进行y(x) = c × c × c × x 的乘法运算,但是同样的处理可以由y(x) = ax(注意,a = c 3 )这一次乘法运算(即没有隐藏层的神经网络)来表示。如本例所示,使用线性函数时,无法发挥多层网络带来的优势。因此,为了发挥叠加层所带来的优势,激活函数必须使用非线性函数。
2.2.4 ReLU函数


def relu(x):
return np.maximum(0,x)
三、3层神经网络的实现

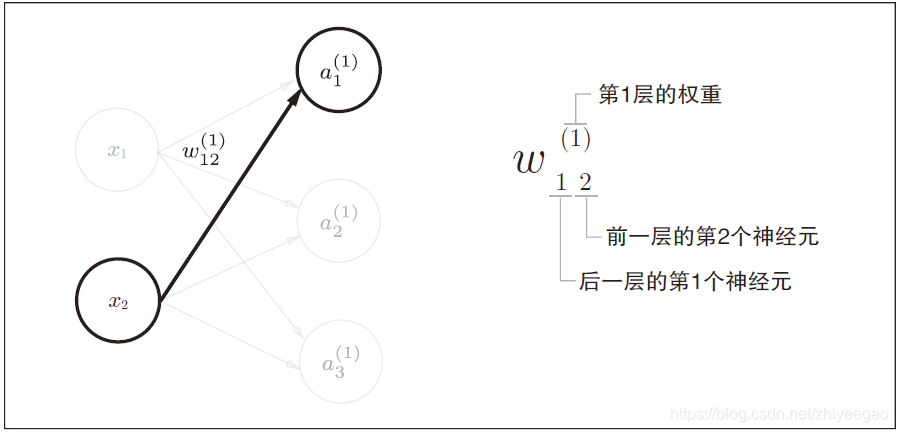









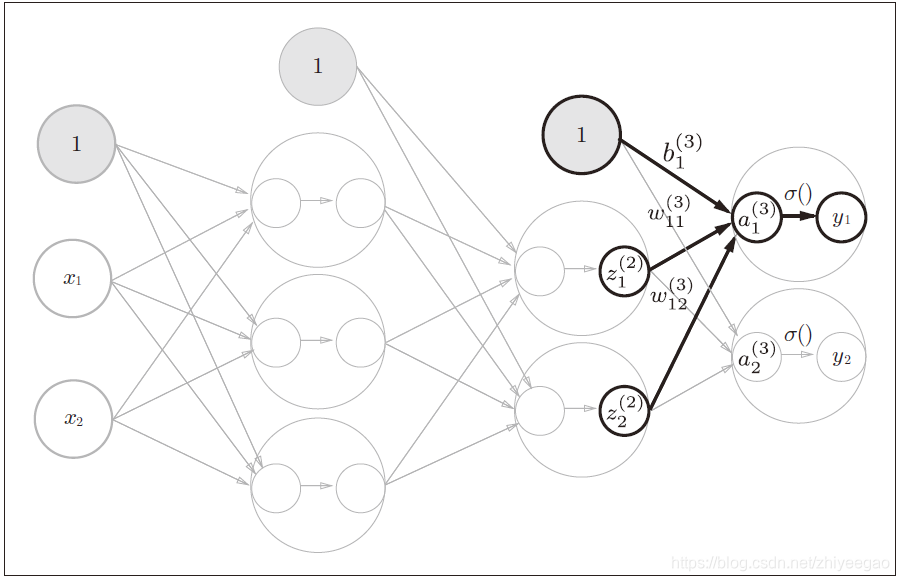







 本文深入探讨了神经网络的基本概念,包括神经网络的结构、权重学习及激活函数的应用。介绍了神经网络如何通过自动调整权重参数从数据中学习,并详细解析了常见的激活函数,如sigmoid、ReLU及其在神经网络中的作用。
本文深入探讨了神经网络的基本概念,包括神经网络的结构、权重学习及激活函数的应用。介绍了神经网络如何通过自动调整权重参数从数据中学习,并详细解析了常见的激活函数,如sigmoid、ReLU及其在神经网络中的作用。
















 5229
5229

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








