全网最细致，轻松搞懂机器学习、深度学习(二)

想要学习机器学习和深度学习，首先需要弄明白一个概念: "损失函数"

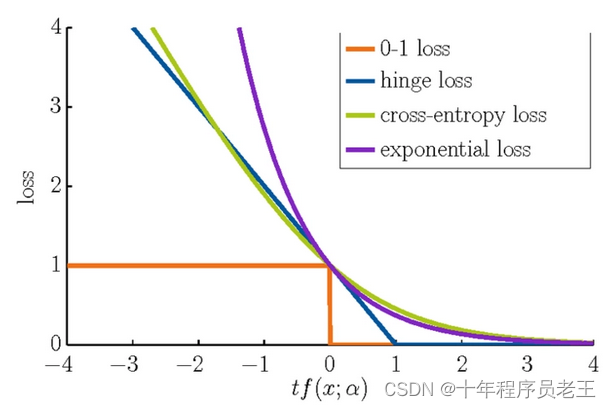
1.什么是损失函数？

        它是评估我们训练出的模型的预测误差的函数，损失函数值越接近0，模型预测的越准确。

例子1

我们想要训练一个模型来预测股票收益。
   首先我们需要大量的市场数据来供模型训练(准备一个训练数据集)

   影响股票收益的因素包括：
       1.公司基本面：公司盈利能力、成长性、财务状况等。
       2.宏观经济因素：GDP增长、通胀率、利率等宏观经济指标。
       3.行业因素：行业发展趋势、竞争格局等。
       4.技术因素：技术创新、行业变革等。
       5.市场情绪：投资者情绪、市场热点等

    这5个因素都有自己的权重，也就是他们对最终股票收益的影响价值不同，我们给5个权重各自分配一个初始权重系数(根据经验分配)，依次是W1 W2 W3 W4 W5，
    那么

预测最终收益 = 公司基本面 * W1 + 宏观经济因素 * W2 + 行业因素 * W3 + 技术因素 * W4 + 市场情绪 * W5

预测误差 = 真实股票收益 - 预测最终收益

损失函数可以定义为lossFunction = 真实股票收益 - 公司基本面 * W1 + 宏观经济因素 * W2 + 行业因素 * W3 + 技术因素 * W4 + 市场情绪 * W5

前面这些被称为前向传播，而后计算(公司基本面、宏观经济因素、行业因素、技术因素、市场情绪)的梯度，再将权重W1 W2 W3 W4 W5减去 "学习率" * 梯度(一般0.01)，

更新后的权重W = W - 学习率 * 梯度

这一步称为反向传播。最终使lossFunction的损失值越来越接近0。

梯度下降：

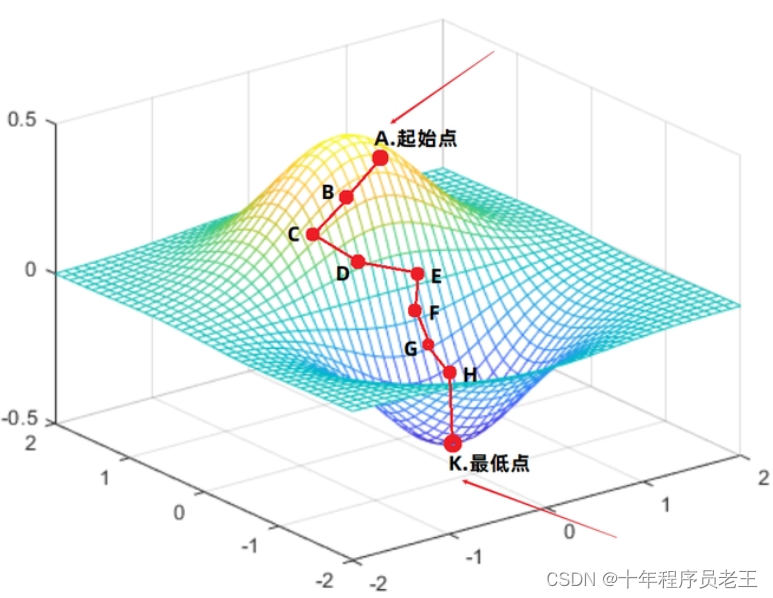
学习率为什么设置的比较低？
	1.稳定性：低学习率可以帮助模型更加稳定地进行训练，避免参数的大幅度变动。这样可以防止模型在训练过程中产生震荡或不稳定的情况。
	2.收敛性：较低的学习率可以帮助模型更好地找到最优解。相比较较高的学习率，它更加靠近最优点，并有更大的概率能够找到全局最优点或者局部最优点。
	3.避免错过最优点：低学习率在接近最优点时会细致地搜索参数空间，减少错过最优解的可能性。它能够更慎重地进行参数的更新，避免错过或跳跃过最优点。

例子2

让看另一个利用模型二分类的问题：我们有一张灰度图片(灰度图片由很多像素点组成，每个像素点只有一个灰度值表示亮度)，我们想通过模型判断它是一只猫，还是一只狗。
根据已有模型预测的过程：
    

假设我们有一个已经训练好的模型model(具体训练过程下面介绍)
1.我们首先进行特征提取，提取出图像中的特征。这些特征表示图片中的边缘、纹理、形状等信息。最终会得到一系列的特征图(假设这个特征图是2080*1080的表格，每个单元格是这个像素点的灰度值)
2.然后我们利用模型里的两套权重矩阵，W_cat W_dog,假设权重矩阵和特征图同规格(2080*1080),那么
3.图片为猫的得分 = 求和(特征图像素点的灰度值 * W_cat)
 图片为猫的概率 = Softmax函数(图片为猫的得分)
 图片为狗的得分 = 求和(特征图像素点的灰度值 * W_dog)
 图片为狗的概率 = Softmax函数(图片为狗的得分)
4.最终哪一个概率高，就判断图片为什么类型

模型训练过程：

1.首先整理一批数据集，分为两个文件夹：猫图片文件夹，狗图片文件夹
2.初始化权重矩阵W_cat(2080*1080)和W_dog(2080*1080) 注：可以使用随机数
3.定义损失函数 lossFunction = 1 -  图片为猫的概率
4.循环猫图片文件夹，训练W_cat权重矩阵，
    5.从当前循环中的这个图片中提取特征(图片中的边缘、纹理、形状等信息)
    6.图片为猫的得分 = 求和(特征图像素点的灰度值 * W_cat)
    7.图片为猫的概率 = Softmax函数(图片为猫的得分)
    8.损失函数值 = 1 -  图片为猫的概率
    9.计算W_cat每个权重的梯度
    10.更新权重：W_cat每个权重 = W_cat每个权重 - 学习率 * 梯度
    (从而实现权重越调越准确，损失函数值逐渐缩小。训练W_dog同理)

2.有哪些损失函数

(1) Probabilistic losses(概率损失函数)

BinaryCrossentropy class：二分类交叉熵损失函数类。用于衡量二分类问题中，预测结果与真实标签之间的差异。

keras.losses.BinaryCrossentropy(
			from_logits=False,
			label_smoothing=0.0,
			axis=-1,
			reduction="sum_over_batch_size",
			name="binary_crossentropy",
)

计算真实标签和预测标签之间的交叉熵损失。
将此交叉熵损失用于二进制（0 或 1）分类应用。 损失函数需要以下输入：
y_true（true label）：此值为 0 或 1。
y_pred（预测值）：这是模型的预测，即单个 浮点值，表示 logit，（即 [-inf， inf] 中的值） 当 ） 或概率（即 [0.， 1.] 中的值 when ）。from_logits=Truefrom_logits=False
		
【参数】
	from_logits：当from_logits为False时，表示模型输出的是经过激活函数（sigmoid）处理后的概率值，内部不再进行激活函数的处理(如sigmoid激活函数的处理)。当from_logits为True时，表示模型输出的是未经过激活函数处理的原始输出值，这些原始输出值被称为“logits”。在这种情况下，损失函数会在内部使用sigmoid函数进行逻辑转换，然后再计算损失。

	label_smoothing：浮点在 [0， 1] "label_smoothing"是一种用于改善分类模型训练的技术。它是一个介于0到1之间的参数，用来调整目标标签（ground truth）的分布。在传统的分类任务中，我们通常使用独热编码来表示目标标签。例如，如果有10个类别，那么目标标签就是一个由10个元素组成的向量，只有正确类别对应的元素为1，其他元素都为0。然而，独热编码假设我们对于每个样本都是100%确定其分类的，但在实际情况下，我们可能存在一些不确定性。这就是"label_smoothing"可以帮助我们处理的地方。
	当"label_smoothing"参数设置为0时，表示我们不对目标标签进行任何平滑处理，即使用传统的独热编码。这意味着模型训练时，会强制要求模型对每个样本进行精确的分类。
	当"label_smoothing"参数设置为一个介于0到1之间的值时（通常很小），我们就开始对目标标签进行平滑处理。这意味着我们会将一部分的置信度从正确的类别分配给其他类别，以使模型更容忍对于不确定性的样本。
	具体说，对于每个目标标签，会将一部分的置信度从正确的类别减去，并等比例地分配给其他类别。这样，模型在训练过程中就会更加平滑地处理分类的不确定性，提升模型的泛化能力。

	axis：计算交叉熵的轴（要素轴）。 默认为 。-1
	在机器学习中，"axis"参数用于指定操作应该在哪个维度上进行。当"axis"为-1时，表示操作应该沿着最后一个维度进行。
	举个例子来说，如果有一个形状为(3, 4, 2)的张量(长宽高)，其中三个维度分别是轴0、轴1和轴2。如果我们进行某个操作时将"axis"设置为-1，那么操作将在最后一个维度上执行，也就是在高度上进行计算、聚合或其他操作。
	reduction：应用于损失的减少类型。
	在深度学习中，常常需要计算损失函数的值。这个损失函数通常是针对一个批次（batch）中多个样本的，而不是仅针对单个样本。
	当使用"reduction"参数时，可以决定如何计算批次上的损失函数。
	当"reduction"设置为"sum_over_batch_size"时，表示在计算损失函数时，会对批次上的损失进行求和，然后再除以批次大小，得到平均损失值。
	具体来说，如果一个批次有N个样本，每个样本的损失函数为L1, L2, ..., LN，那么使用"reduction='sum_over_batch_size'"时，计算的损失函数值为：(L1 + L2 + ... + LN) / N。
	这种方式在训练时通常用于计算损失函数的平均值，使得不同批次的损失函数可以进行合理比较，并且可以消除批次大小对结果的影响。
	其他常见的"reduction"参数值还有：
		"none"：不进行任何降维操作，返回一个与输入形状相同的损失值向量。
		"sum"：对批次上的损失进行求和，得到一个标量值。
		"mean"：对批次上的损失求平均，得到一个标量值。

name：损失实例的可选名称。


【代码示例】
	推荐用法：（套from_logits=True)
	使用 API：compile()
	model.compile(
		loss=keras.losses.BinaryCrossentropy(from_logits=True),
		...
	)
	作为独立功能：

	>>> # Example 1: (batch_size = 1, number of samples = 4)
	>>> y_true = [0, 1, 0, 0]
	>>> y_pred = [-18.6, 0.51, 2.94, -12.8]
	>>> bce = keras.losses.BinaryCrossentropy(from_logits=True)
	>>> bce(y_true, y_pred)
	0.865
	>>> # Example 2: (batch_size = 2, number of samples = 4)
	>>> y_true = [[0, 1], [0, 0]]
	>>> y_pred = [[-18.6, 0.51], [2.94, -12.8]]
	>>> # Using default 'auto'/'sum_over_batch_size' reduction type.
	>>> bce = keras.losses.BinaryCrossentropy(from_logits=True)
	>>> bce(y_true, y_pred)
	0.865
	>>> # Using 'sample_weight' attribute
	>>> bce(y_true, y_pred, sample_weight=[0.8, 0.2])
	0.243
	>>> # Using 'sum' reduction` type.
	>>> bce = keras.losses.BinaryCrossentropy(from_logits=True,
	...     reduction="sum")
	>>> bce(y_true, y_pred)
	1.730
	>>> # Using 'none' reduction type.
	>>> bce = keras.losses.BinaryCrossentropy(from_logits=True,
	...     reduction=None)
	>>> bce(y_true, y_pred)
	array([0.235, 1.496], dtype=float32)
	默认用法：（setfrom_logits=False)

	>>> # Make the following updates to the above "Recommended Usage" section
	>>> # 1. Set `from_logits=False`
	>>> keras.losses.BinaryCrossentropy() # OR ...('from_logits=False')
	>>> # 2. Update `y_pred` to use probabilities instead of logits
	>>> y_pred = [0.6, 0.3, 0.2, 0.8] # OR [[0.6, 0.3], [0.2, 0.8]]		
		   

BinaryFocalCrossentropy class：二分类焦点交叉熵损失函数类。与二分类交叉熵类似，但引入焦点机制，可以减轻训练样本类别不平衡的问题。

CategoricalCrossentropy class：多分类交叉熵损失函数类。用于衡量多分类问题中，预测结果与真实标签之间的差异。

CategoricalFocalCrossentropy class：多分类焦点交叉熵损失函数类。与多分类交叉熵类似，引入焦点机制以解决训练样本类别不平衡的问题。

SparseCategoricalCrossentropy class：稀疏多分类交叉熵损失函数类。适用于多分类问题中，标签以稀疏表示（整数形式）的情况。

Poisson class：泊松损失函数类。用于泊松分布相关的任务，例如计数数据的建模。

binary_crossentropy function：二分类交叉熵损失函数。与BinaryCrossentropy class类似，但以函数的形式提供。

categorical_crossentropy function：多分类交叉熵损失函数。与CategoricalCrossentropy class类似，但以函数的形式提供。

sparse_categorical_crossentropy function：稀疏多分类交叉熵损失函数。与SparseCategoricalCrossentropy class类似，但以函数的形式提供。

poisson function：泊松损失函数。与Poisson class类似，但以函数的形式提供。

KLDivergence class：KL散度（Kullback-Leibler divergence）损失函数类。用于衡量两个概率分布之间的距离。

kl_divergence function：KL散度损失函数。与KLDivergence class类似，但以函数的形式提供。

CTC class：联结时序分类（Connectionist Temporal Classification）损失函数类。用于序列识别任务，例如语音识别或文本识别。

(2) Regression losses(回归损失)

MeanSquaredError class：均方误差损失函数类。用于衡量预测值与真实值之间的平均平方差，是最常用的回归损失函数。

MeanAbsoluteError class：平均绝对误差损失函数类。用于衡量预测值与真实值之间的平均绝对差。

MeanAbsolutePercentageError class：平均绝对百分比误差损失函数类。用于衡量预测值与真实值之间的平均绝对百分比差。

MeanSquaredLogarithmicError class：均方对数误差损失函数类。用于衡量预测值的对数和真实值的对数之间的平均平方差。

CosineSimilarity class：余弦相似性损失函数类。用于衡量预测向量和真实向量之间的余弦相似度，可以衡量它们的方向和相似程度。

mean_squared_error function：均方误差损失函数。与MeanSquaredError class类似，但以函数的形式提供。

mean_absolute_error function：平均绝对误差损失函数。与MeanAbsoluteError class类似，但以函数的形式提供。

mean_absolute_percentage_error function：平均绝对百分比误差损失函数。与MeanAbsolutePercentageError class类似，但以函数的形式提供。

mean_squared_logarithmic_error function：均方对数误差损失函数。与MeanSquaredLogarithmicError class类似，但以函数的形式提供。

cosine_similarity function：余弦相似性损失函数。与CosineSimilarity class类似，但以函数的形式提供。

Huber class：Huber损失函数类。是一种在平方误差和绝对误差之间平衡的损失函数，对异常值具有鲁棒性。

huber function：Huber损失函数。与Huber class类似，但以函数的形式提供。

LogCosh class：Log-Cosh损失函数类。在平方误差和绝对误差之间取中间值，并具有平滑的特性，对异常值有较小的敏感性。

log_cosh function：Log-Cosh损失函数。与LogCosh class类似，但以函数的形式提供。

(3) Hinge losses(最大间隔分类:旨在通过找到能够将不同类别的样本尽可能分开的决策边界来进行分类)

Hinge class（铰链类）是通过铰链损失函数实现的二分类器。

SquaredHinge class（平方铰链类）是一种基于平方铰链损失函数的二分类器。与普通的铰链损失函数不同，平方铰链损失引入了一个平方项，可以对错误分类的样本施加更大的惩罚。

CategoricalHinge class（分类铰链类）是用于多类别分类问题的铰链损失。它在训练多类别分类器时计算每个类别之间的铰链损失。

hinge function（铰链函数）是一个用于计算单个样本的铰链损失值的函数。它接受样本的真实标签和预测分数，并返回相应的损失值。铰链函数可用于二分类或多分类问题。

squared_hinge function（平方铰链函数）是一个用于计算平方铰链损失值的函数。它使用的计算方式与普通的铰链函数类似，但引入了平方项。

categorical_hinge function（分类铰链函数）是一个用于计算分类铰链损失值的函数。它用于多类别分类任务，计算每个类别的铰链损失，并返回总的损失值。