数据运营系列（三）：熵权法如何确定指标权重构建评价体系

1. 熵权法

信息论基本原理解释信息是系统有序性的度量单位，而熵可以度量系统的无序程度；如果某个指标的信息熵越小，该指标提供的信息量越大，指标变异程度(方差)高，因此在综合评价中所起作用理当越大，权重就应该越高。熵权法的基本原理就是根据指标变异性的大小来确定客观权重。一般来说，这个方法相比于AHP专家打分更客观。熵权法确定指标权重的推导过程如下：

第一步：数据标准化

将各个指标的数据进行标准化处理。假设给定了k个指标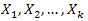，其中。假设对各指标数据标准化后的值为，那么

第二步：求各指标的信息熵

根据信息论中信息熵的定义，一组数据的信息熵计算为：

，其中

第三步：确定各指标权重

根据信息熵的计算公式，计算出各个指标的信息熵为。通过信息熵计算各指标的权重：

2. 评价体系之确定指标权重并计算样本得分

比如最近某快递公司在多地设置了快递点，但是快递点运营状态如何从数据上来获知，有哪些快递点需要取消，哪些快递点需要扩大经营？如何为给出每个快递点的具体得分，从而设置奖惩制度。这里建立一个评价体系，评价体系中包括能很好衡量快递点经营效果的指标，每个快递点都有这些指标的数据，因为熵权法可以自己计算出各个指标的权重，那么避免了专家打分法等主观权重带来的偏见，因此从该数据基础上即可获得各个快递点的得分。

熵权法计算过程：

求解过程放在了Excel，公众号后台回复“熵权法”即可获取。

第一步：数据标准化。假设有11个快递点参与评价，评价体系中包括以下7个子指标，以下指标数据通过归一化公式已实现数据标准化。

表1 数据标准化

第二步：求各指标的信息熵

表2 求解各数据的Pij

表3 求解信息熵Ei

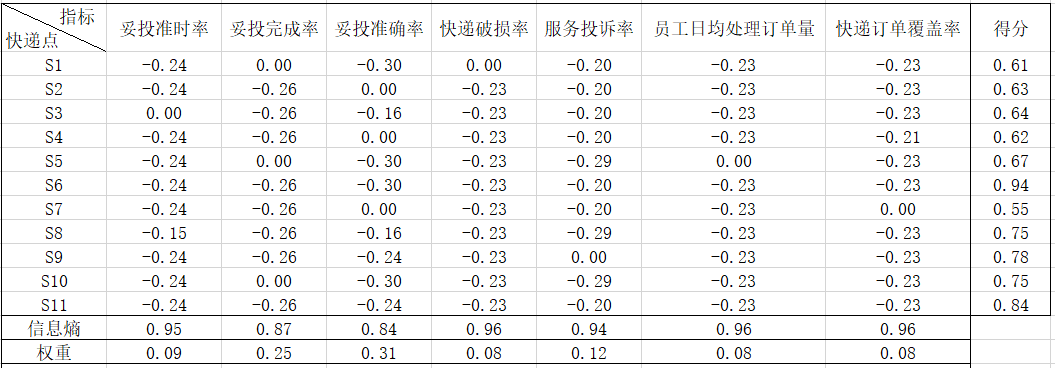
第三步：求各指标权重，见表3倒数第一行。

第四步：各快递点得分，见表3最后一列。可以看到快递点S6得分最高。

热门文章

直戳泪点！数据从业者权威嘲讽指南！

数据分析师做成了提数工程师，该如何破局？

全栈型VS专精型，团队到底需要什么样的人？

数据驱动业务，比技术更重要的是思维的转变

最近面了十多个数据分析师，聊一聊我发现的一些问题

【您的在看，我的莫大鼓励】