每日一题 LeetCode

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/binary-tree-right-side-view/solution/er-cha-shu-de-you-shi-tu-by-leetcode-solution/

二叉树的右视图

题目描述

题解

二叉树层次层数即为右视图的节点数。

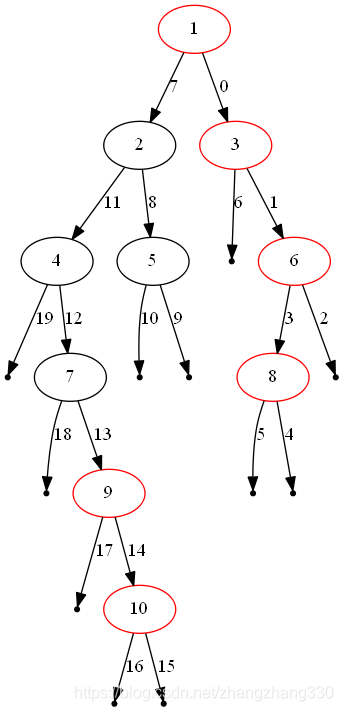
方法一：深度优先搜索DFS

DFS总是先搜索到最右子树，每一层最先访问到最右边的节点。存储在每个深度访问的第一个结点，根据树的层数得到最终的结果数组。

复杂度分析
时间复杂度 : $O(n)$。深度优先搜索最多访问每个结点一次，因此是线性复杂度。
空间复杂度 : $O(n)$。最坏情况下，栈内会包含接近树高度的结点数量，占用 $O(n)$ 的空间。

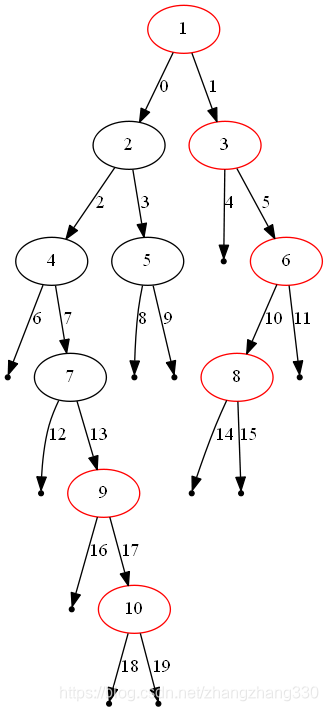
方法二：广度优先搜索BFS

用广度优先搜索实现二叉树的层次遍历。
执行广度优先搜索，左结点排在右结点之前，对每一层都从左到右访问。因此，只保留每个深度最后访问的结点，就可以在遍历完整棵树后得到每个深度最右的结点。简言之，相对于方法一，除了将栈改成队列，并去除了rightmost_value_at_depth之前的检查外，算法没有别的改动。

复杂度分析
时间复杂度 : $O(n)$。 每个节点最多进队列一次，出队列一次，因此广度优先搜索的复杂度为线性。
空间复杂度 : $O(n)$。每个节点最多进队列一次，所以队列长度最大不不超过 n，所以这里的空间代价为 $O(n)$。

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        unordered_map<int, int> rightmostValueDepth;
        int maxDepth = -1;
        /*
    //方法一：DFS
        stack<TreeNode*> nodeStack;
        stack<int> depthStack;
        nodeStack.push(root);
        depthStack.push(0);

        while(!nodeStack.empty()){
            TreeNode* node = nodeStack.top();
            nodeStack.pop();
            int depth = depthStack.top();
            depthStack.pop();

            if(node != NULL){
                maxDepth = max(maxDepth, depth);

                if(rightmostValueDepth.find(depth) == rightmostValueDepth.end()){
                    rightmostValueDepth[depth] = node->val;
                }
                nodeStack.push(node->left);
                nodeStack.push(node->right);
                depthStack.push(depth + 1);
                depthStack.push(depth + 1);

            }
        }
        */

        // 方法二：BFS
        queue<TreeNode*> nodeQueue;
        queue<int> depthQueue;
        nodeQueue.push(root);
        depthQueue.push(0);
        
        while(!nodeQueue.empty()){
            TreeNode* node = nodeQueue.front();
            nodeQueue.pop();
            int depth = depthQueue.front();
            depthQueue.pop();

            if(node != NULL){
                maxDepth = max(maxDepth,depth);

                rightmostValueDepth[depth] = node->val;

                nodeQueue.push(node->left);
                nodeQueue.push(node->right);
                depthQueue.push(depth + 1);
                depthQueue.push(depth + 1);
            }
        }
        vector<int> rightView;
        for(int depth = 0; depth <= maxDepth; depth++){
            rightView.push_back(rightmostValueDepth[depth]);
        }
        return rightView;
    }
};

小结

深度/广度优先遍历图，时间/空间复杂度为线性时间。
一般步骤：
顶点出发⇒ 深度/广度优先遍历⇒ 回溯