洛谷动态规划python-最长公共子序列

动态规划算法通常用于求解具有某种最优性质的问题，在这类问题中，可能会有许多可行解。其思想实质是分治思想和解决冗余。适合动态规划法求解的问题，经分解得到的各个子问题往往不是相互独立的。在求解过程中，将已解决的子问题的解进行保存，在需要的时候可以轻松找出。这样就避免了大量无意义的重复计算。
基本要素：
1.最优子结构性质
2.子问题重叠性质
3.自底向上的求解方法

P1216 [USACO1.5][IOI1994]数字三角形 Number Triangles

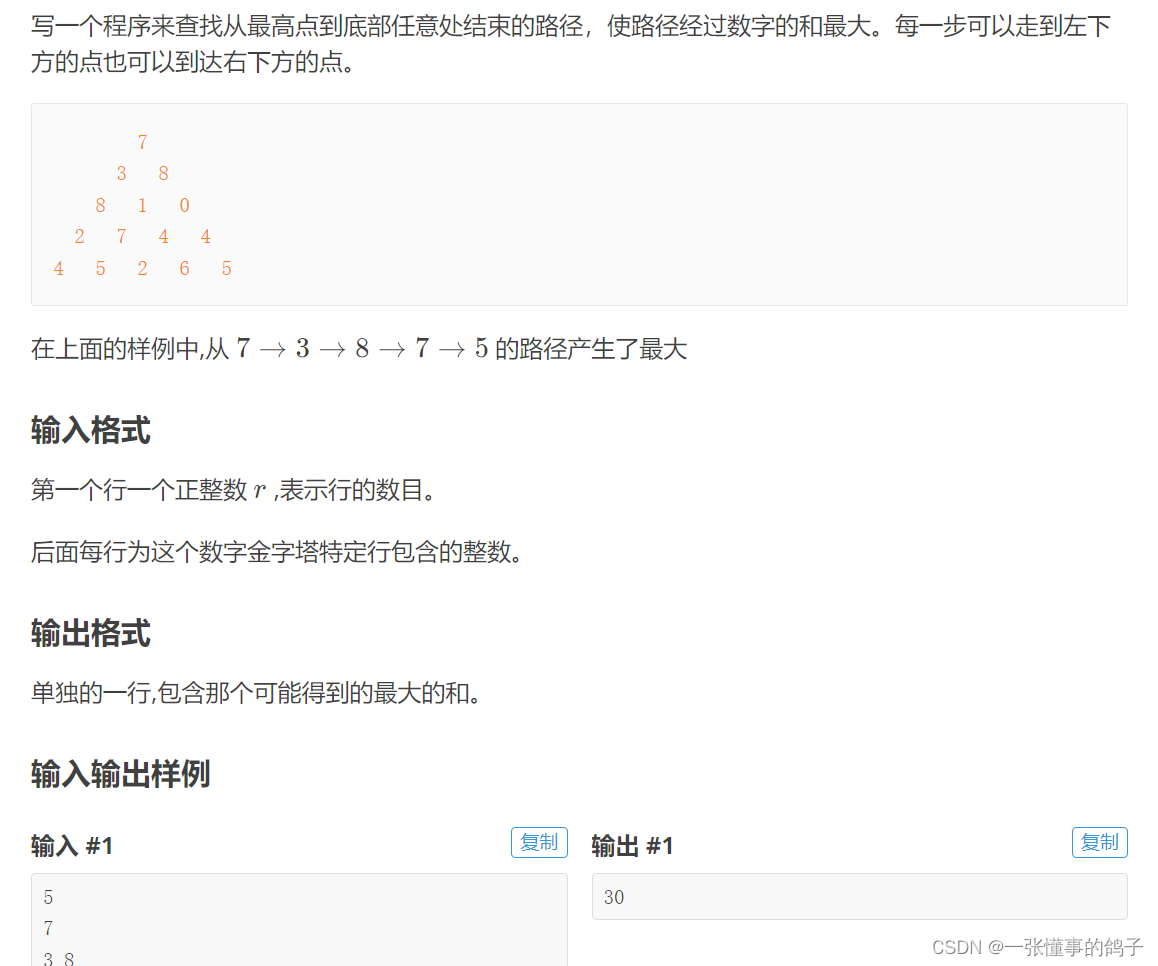
list_two = [[0] * 2] * 2#浅拷贝

使用列表创建一个二维数组，可以使用生成器来辅助实现

从下往上

r=int(input())
arr=[[0 for i in range(1001)] for i in range(1001)]
for i in range(r):
        arr[i]=input().split()
        arr[i] = [int(j) for j in arr[i]]
i=r-2
#扫描除最后一排前的所有数
while i>=0