二叉搜索树（BST）删除节点--思路清晰

前言：在学习BST时，发现查找插入等操作都很好理解和实现，而删除节点的操作情况比较复杂，故通过自己的理解整理如下，本文适合初学者理解并自己动手实现BST删除操作。

在很多文章中提到，删除节点可以考虑以下三种情况：

1. 没有左右子节点
2. 存在左节点或者右节点
3. 同时存在左右子节点

这种思路是最简单的思路很好理解，但是实现起来会发现代码有点冗杂。在本文中，将按照以下思路来进行讲解：

1. 没有左子树（包括了没有左子树有右子树，没有左子树也没有右子树）
2. 有左子树但没有右子树
3. 既有左子树，又有右子树

首先，我们来想一下删除一个单链表的节点该如何操作？（1）找到要删除的节点，（2）记录该节点的前一个节点（3）将前一节点链接到该节点的后一节点。这样就将该节点所隔离，根据java的垃圾回收机制，该节点将被删除回收内存。

那么如果二叉树就像一个单链表一样，那不是就很好解决了？所以删除二叉树节点的基本情况就是要删除的节点没有左子树，或者没有右子树（current.left==null || current.right==null），这时少了一路分支，处理起来就像单链表一样，分为三步：（1）找到要删除的节点（2）记录该节点的父节点（3）将父节点链接到该节点的后一节点。但是在执行第三步的时候要注意：父节点有left和right两个指针，需要判断是哪个指针，也就是current是父节点的左子树还是右子树；该节点的后一节点就是那个唯一的不为空的节点。

情况一：没有左子树

情况二：有左子树没有右子树

下图分别给出了要删除的节点只有右子树，只有左子树，左右子树都没有（叶子节点）的情况。

         

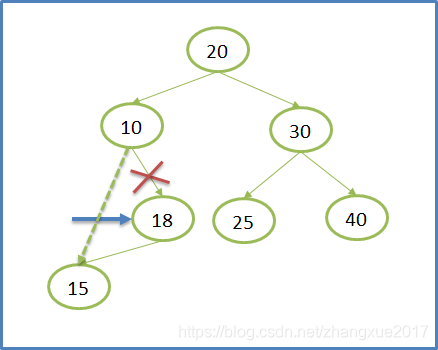
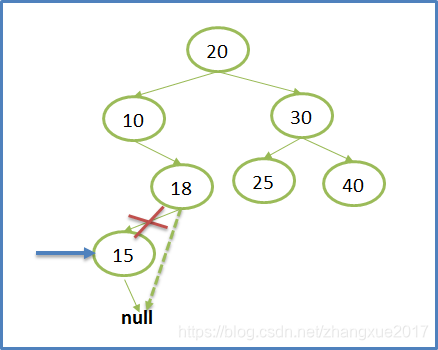
下面给出基本情况的代码：

        //cur指向要被删除的节点
        if(cur==null)
            return false;
        //第一种情况：没有左子树（包括了没有做子树有右子树，没有左子树也没有右子树）
        if(cur.left==null){
            if(parent==null){//特殊情况：根节点
                root=cur.right;
            }
            else{
                if(e.compareTo(parent.val)<0)//cur是parent的左子节点
                    parent.left=cur.right;
                else//cur是parent的右子节点
                    parent.right=cur.right;
            }
        }
        //情况二：有左子树没有右子树
        else if(cur.right == null){
            if(parent==null){//根节点
                root=cur.left;
            }
            else{
                if(e.compareTo(parent.val)<0)//cur是parent的左子节点
                    parent.left=cur.left;
                else//cur是parent的右子节点
                    parent.right=cur.left;
            }

        }
        else{
        //稍后添加
          return false;
        }

情况三：有左子树，又有右子树；

这时如果单纯地将父节点连接到该节点的左子节点或者右子节点都会导致另外一个子树没有被链接而被删除，所以我们要找到一个合适的值来代替该节点的位置，再删除这个值。什么是一个合适的值？（1）该值要确保BST树的基本性质，也就是说放在要删除节点的位置上，大于它的左节点而小于他的右节点(2)该值应该是前面的基本情况中的一种，也就是说没有左子树，或者没有右子树。所以方法有两种：从当前节点的左子节点的右子树中找出最大值，也就是最右节点（没有右子树）；或者从当前节点的右子节点的左子树中找出最小值，也就是最左节点（没有左子树）；下面给出第三种情况的思路图：

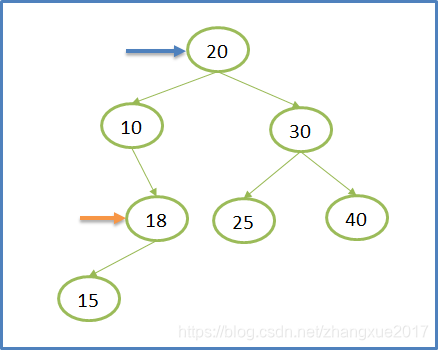
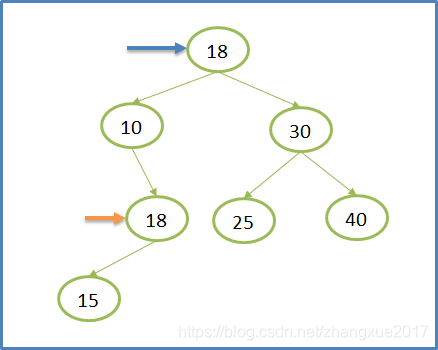
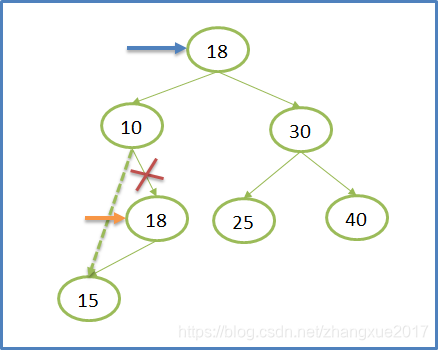
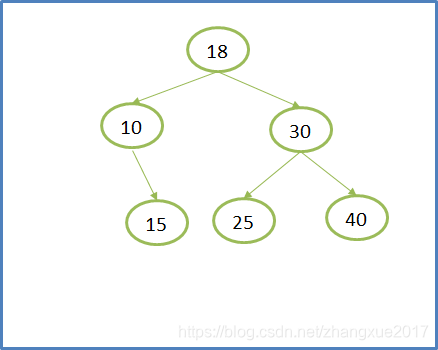
第一步：定位到要删除20这个节点，发现属于情况三；第二步：找到该节点左子树的最大值（最右节点），为18；第三步：将18复制到要删除的节点处；第四步：将18的父节点的右子节点（因为18是父节点的右子节点）链接到18的左子节点（最右节点没有右子节点）。

下面给出完整的代码：

    public boolean delete(E e){
        TreeNode<E> parent=null;
        TreeNode<E> cur=root;
        //首先定位要删除节点的位置
        while(cur!=null){
            if(e.compareTo(cur.val)<0){
                parent=cur;
                cur=cur.left;
            }
            else if(e.compareTo(cur.val)>0){
                parent=cur;
                cur=cur.right;
            }
            else
                break;
        }
        //cur指向要被删除的节点
        if(cur==null)
            return false;
        //第一种情况：没有左子树（包括了没有做子树有右子树，没有左子树也没有右子树）
        if(cur.left==null){
            if(parent==null){//根节点
                root=cur.right;
            }
            else{
                if(e.compareTo(parent.val)<0)//cur是parent的左子节点
                    parent.left=cur.right;
                else//cur是parent的右子节点
                    parent.right=cur.right;
            }
        }
        //情况二：有左子树没有右子树
        else if(cur.right == null){
            if(parent==null){//根节点
                root=cur.left;
            }
            else{
                if(e.compareTo(parent.val)<0)//cur是parent的左子节点
                    parent.left=cur.left;
                else//cur是parent的右子节点
                    parent.right=cur.left;
            }

        }
        //情况三：有左子树，又有右子树；
        else{
            TreeNode<E> parentOfRightMost=cur;
            TreeNode<E> rightMost=cur.left;
            //找左子树中的最大值，则需要从左子树的右节点找
            while(rightMost.right!=null){
                parentOfRightMost=rightMost;
                rightMost=rightMost.right;
            }
            //当前要删除节点的左子树下的最右节点是最大值，该值一定大于左子树的值（因为是右节点）
            //并且小于当前节点的右节点的值，因为是左子树下的分支。所以用该值代替要删除的节点，仍然满足左子节点小于根节点，右子节点大于根节点
            cur.val=rightMost.val;
            if(parentOfRightMost.right==rightMost)//这种情况是确实找到了最右节点，也就是说该节点没有右子树，可能有左子树
                parentOfRightMost.right=rightMost.left;//把剩下的子树连接上
            else//这种情况是没有执行while，该节点就是当前节点的左子节点（parentOfRightMost.left），而且没有右子树（rightMost.left）
                parentOfRightMost.left=rightMost.left;
        }
        /*
        else{
            TreeNode<E> parentOfRightMost=cur;
            TreeNode<E> rightMost=cur.right;
            //找右子树中的最小值，则需要从右子树的左节点找
            while(rightMost.left!=null){
                parentOfRightMost=rightMost;
                rightMost=rightMost.left;
            }
            
            cur.val=rightMost.val;
            if(parentOfRightMost.left==rightMost)
                parentOfRightMost.right=rightMost.right;
            else
                parentOfRightMost.left=rightMost.right;
         */
        size--;
        return true;
    }

至此，已经完成了整个删除过程，剩下的大家可以自己写一个代码测试一下这三种情况的删除。