基于SVD图片压缩

基于SVD图片压缩原理:

图片其实就是数字矩阵，通过SVD将该矩阵降维，只使用其中的重要特征来表示该图片从而达到了压缩的目的。

数据集降维：

dim = data.T * U[:,:count] * dig.I # 降维

这里的dig为对角矩阵（需要利用原来svd返回的sigma向量构建矩阵，构建需要使用count这个值）。

U为svd返回的左奇异矩阵，count为我们指定的多少个奇异值，这也是dig矩阵的维数。

重构数据集：

redata = U[:, :count] * dig * VT[:count, :]  # 重构

这里的dig同样为对角矩阵（需要利用原来svd返回的dig向量构建矩阵，构建需要使用count这个值），VT为svd返回的右奇异矩阵，count为我们指定的多少个奇异值（可以按能量90%规则选取或者指定前多少个奇异值）

# *===================================*
# -*- coding: utf-8 -*-
# * Time : 2019-12-10 20:15
# * Author : zhangsf
# *===================================*
from numpy import mat, eye
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import numpy as np

path = './img/1.jpg'

img_eg = mpimg.imread(path)
print(img_eg.shape)
# 奇异值分解
img_temp = img_eg.reshape(600, 599 * 3)
U, sigma, VT = np.linalg.svd(img_temp)
# 在重构之前，依据前面的方法需要选择达到某个能量度的奇异值
cnt = sum(sigma)
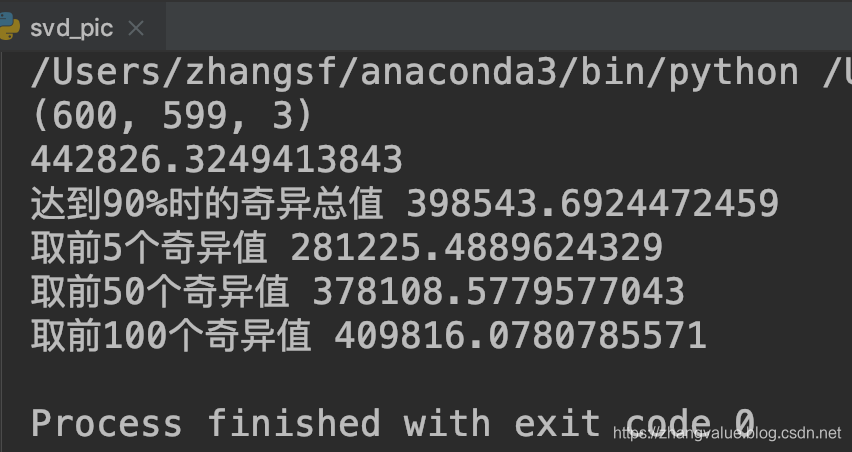
print(cnt)
cnt90 = 0.9 * cnt  # 达到90%时的奇异总值
print("达到90%时的奇异总值",cnt90)
count = 100  # 选择前100个奇异值
cntN = sum(sigma[:count])

print("取前10个奇异值",sum(sigma[:10]))
print("取前50个奇异值",sum(sigma[:50]))
print("取前100个奇异值",sum(sigma[:100]))

# 重构矩阵
dig = mat(eye(count) * sigma[:count])  # 获得对角矩阵
# dim = data.T * U[:,:count] * dig.I # 降维 格外变量这里没有用
redata = U[:, :count] * dig * VT[:count, :]  # 重构
plt.imshow(redata, cmap='gray')  # 取灰
plt.title("nums of sigma = 100")
plt.show()  # 可以使用save函数来保存图片

原图效果

前5个奇异值的图片

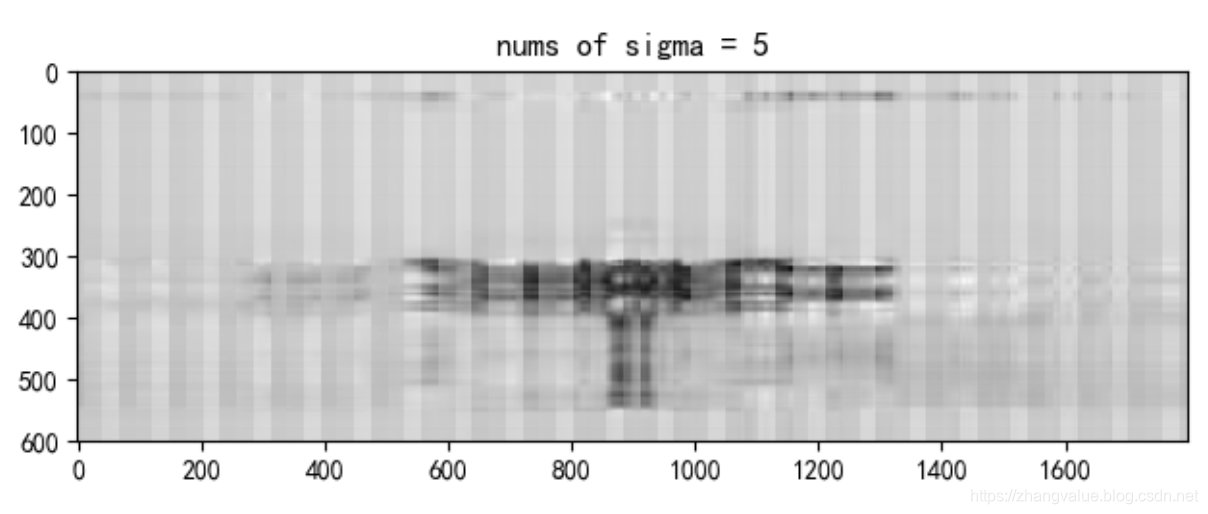
前50个奇异值的图片

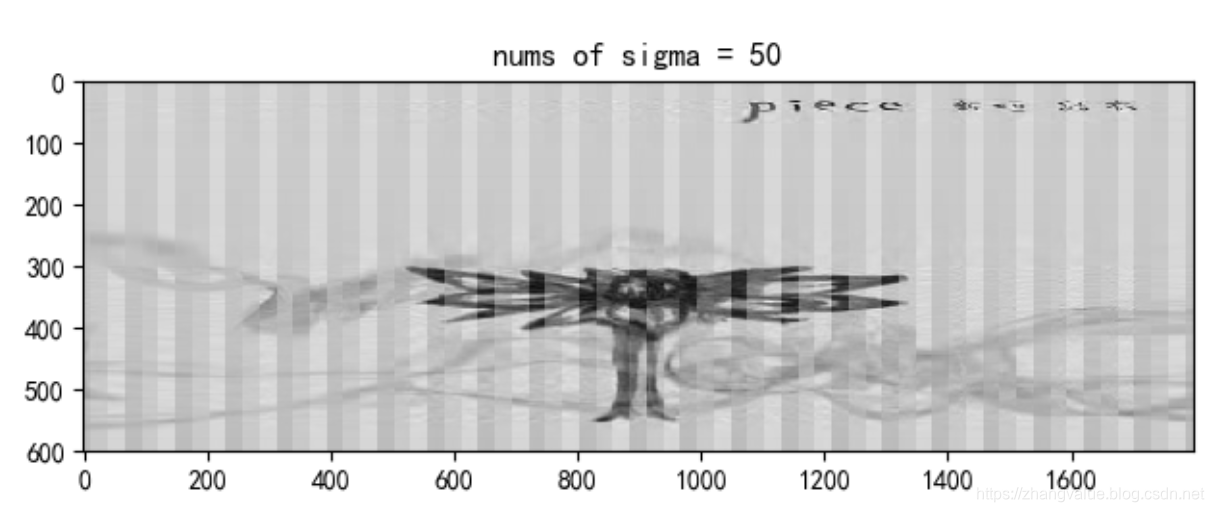
前100个奇异值

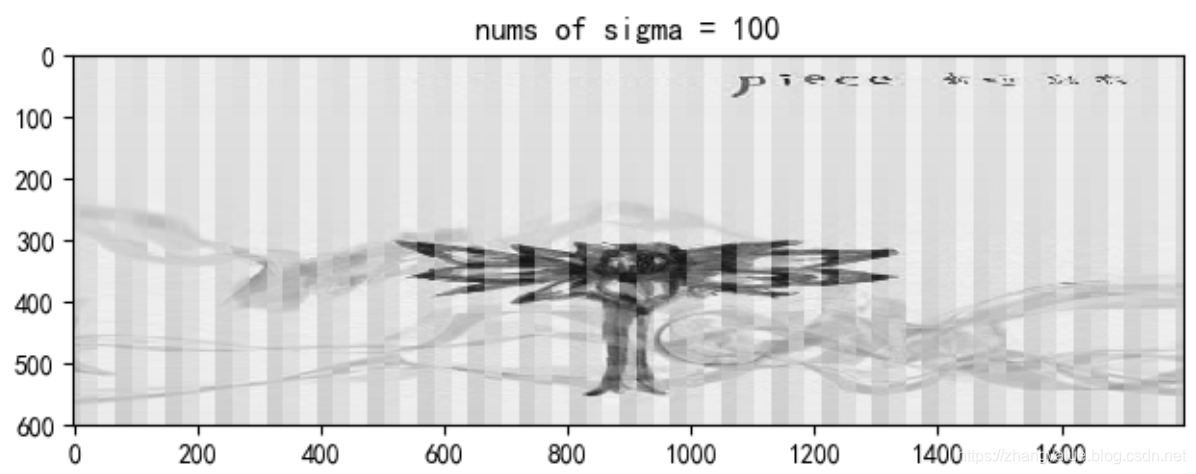
取前 50 个最大奇异值来重构图像时，已经非常清晰了。我们得到和原图差别不大的图像。也就是说，随着选择的奇异值的增加，重构的图像越来越接近原图像。

基于这个原理，奇异值分解可以用来进行图片压缩。

显然，所需存储量大大减小了。在需要存储许多高清图片，而存储空间有限的情况下，就可以利用 SVD，保留奇异值最大的若干项，舍去奇异值较小的项即可。

奇异值从大到小衰减得特别快，在很多情况下，前 10% 甚至 1% 的奇异值的和就占了全部的奇异值之和的 99% 以上了。这样在压缩图片的时候就可以只需要取部分就可以展示出原图片的效果。