https://www.luogu.com.cn/problem/P9510
关于斐波那契和的平方,其实就是正方形的面积和:
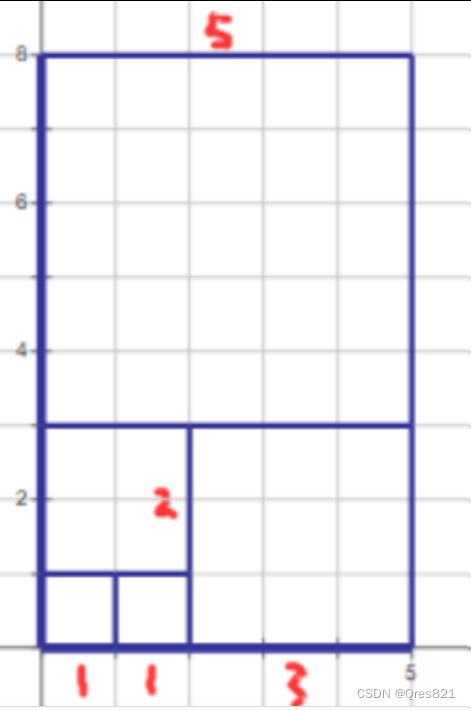
也就是 f ( i ) ∗ f ( i + 1 ) f(i)*f(i+1) f(i)∗f(i+1)
我们现在要求立方,但我们可以可以发现红色部分的结果是一样的:
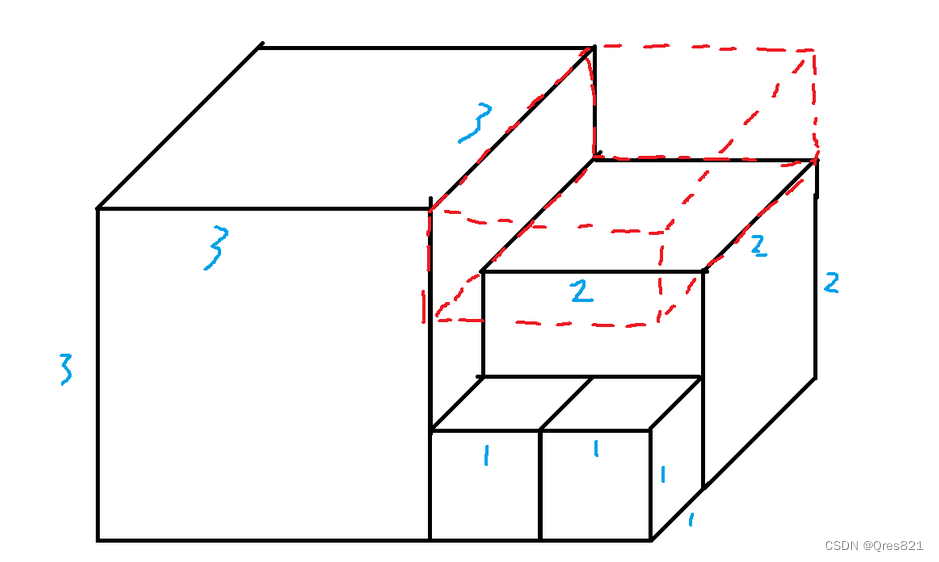
直接三条棱表示除了,就是 f ( i ) ∗ f ( i − 1 ) ∗ f ( i − 2 ) f(i)*f(i-1)*f(i-2) f(i)∗f(i−1)∗f(i−2)。因此我们可以全部约掉(在 立体图形相当于在所有空位全部补上了),所以刚好就是 : f ( i ) 2 ∗ f ( i + 1 ) f(i)^2*f(i+1) f(i)2∗f(i+1)。我们加上外面的常数项直接矩阵快速幂即可。







 本文讨论了如何利用斐波那契数列的性质,将立方问题转化为求平方的乘积,通过矩阵快速幂的方法简化计算,解决与几何图形面积相关的数学问题。
本文讨论了如何利用斐波那契数列的性质,将立方问题转化为求平方的乘积,通过矩阵快速幂的方法简化计算,解决与几何图形面积相关的数学问题。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








