第八讲：产生式模型：NaiveBayes, HMM（上）

5 产生式模型

5.1 产生式模型与判别式模型区别

5.2 朴素贝叶斯

5.2.1 原理与模型

5.2.2 算法

5.2.3 策略

5.2.4 高斯判别分析

5.3 隐马尔科夫模型

5.3.1 模型

5.3.2 推理：概率计算

---

5 产生式模型

5.1 产生式模型与判别式模型区别

 

结束了上节课具有和厦大精神（自强不息、止于至善）一样的boosting，这节课主要介绍了判别式模型（Discriminative Modeling,DM）和产生式模型(Generative Modeling,GM)的区别，朴素贝叶斯以及隐马尔科夫模型。

 

首先，我们来了解一下什么是产生式模型以及判别式模型。

 

 

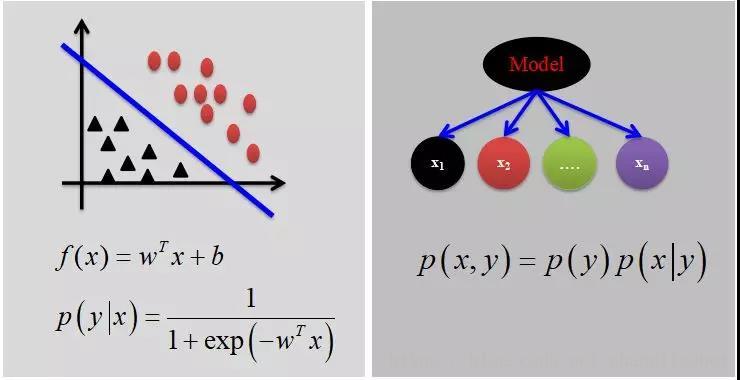
✓ 判别式模型：在一个基本的机器学习问题中，通常有输入，输出两部分，例如对于分类来说，判别模型寻求不同类别之间的最优分类面，估计的是条件概率分布：。

常见的有：

• Logistic Regression

• SVM

• Traditional Neural Networks

• Nearest Neighbor

 

✓ 产生式模型：产生式模型则是对后验概率建模，试图描述x与y的联合分布，估计的是联合概率分布：。

常见的有：

• Naive Bayes

• Mixtures of Gaussians，HMMs

• Markov Random Fields

 

产生vs判别：

产生是模型有其对应的判别式模型，这样的组合叫做“产生式-判别式”对；

判别式模型不一定有其对应的产生式模型；

训练样本多的情况下，采用判别式；

训练样本少的情况下，选择产生式；

产生式模型可以根据贝叶斯公式得到判别式模型，但反过来不行。

 

Andrew Ng在NIPS2001年有一篇专门比较判别模型和产生式模型的文章：On Discrimitive vs. Generative classifiers: A comparision of logistic regression and naive Bayes ，感兴趣的同学也可以看一下~

5.2 朴素贝叶斯

5.2. 1原理与模型

 

前面几讲都是关于判别式模型的内容，从本讲开始将会为大家介绍一些产生式模型，接下来的朴素贝叶斯和隐马尔科夫模型都属于产生式模型。

 

朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的训练数据集，首先基于特征条件独立假设学习输入/输出的联合概率分布；然后基于此模型，对于给定的输入x，利用贝叶斯定理求出后验概率最大的输出y。朴素贝叶斯法实现简单，学习与预测的效率都很高，是一种常用的方法。

5.2.2 算法

 

假设现在我们有了一些数据D，标签为0或者1。

对于新来的数据x，若想预测它的标签值，我们可以采用判别模型，例如logistic回归去找到一条决策边界，来区分是0还是1，当然我们也可以用产生式模型，例如朴素贝叶斯，根据训练集中label为1的样本，我们可以建立label=1的模型，然后对于新来的样本，我们可以让它与label=1的模型进行匹配看看概率有多少，与label=0的模型进行匹配看概率多大，哪一个概率大即为预测标签。这种做法的形式化写法：

 

根据贝叶斯公式：

 

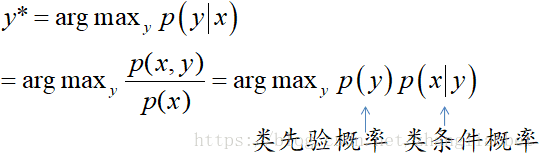
其中：

 

 

假设我们要解决的是二分类问题，各维度都是离散的值， 种可能。那我们要求解的参数有多少个呢？

 

以下推导基于这样两个假设：

 

 

假设 1，各个维度相互独立，这是一个较强的假设，这是“Naive”的由来，由于一般特征维度较大，这么多特征的联合概率分布建模非常吃力，于是就有了一个非常Naive的假设，即所有特征之间是相互独立的，根据独立性的定义，联合概率可以写成每个特征各自的条件概率的乘积：

假设 2，为推导简便。

那么具体的我们需要求解哪些参数呢？

模型参数被大大缩减。如何求解这些参数呢？

 

因为我们假设的是做二分类，可用伯努利分布来刻画：

 

则 

同理对于其余参数，有：

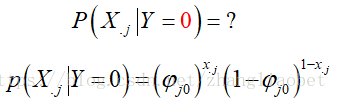
即：

似然函数：

取对数：

应用极大似然估计求参数：

令 ln L 分别对各参数求偏导，并令偏导数为零，即：

得：

 

进一步的：

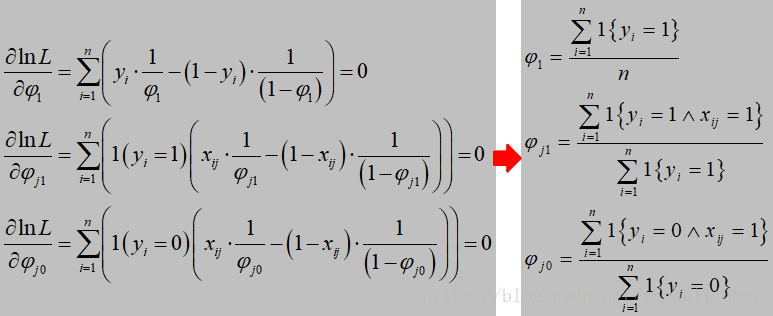
可以看到，各个参数的计算其实非常简单，就是数数。下面我们通过一两个简单的实例来看看它到底是怎么计算的。

 

例一：

 

由图可知，一共有15个样本，其中，

现在要问x1=2,x2=S的标签是什么？

求解： 

其余参数计算方式同上，有：

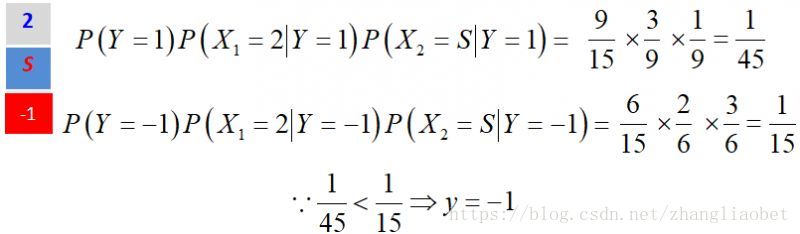
因此，x1=2，x2=S的样本标签为-1。

 

例二:

 

由图可知，一共有六个样本，P为垃圾邮件的概率为4/6 ,P为正常邮件的概率为2/6 。

 

右边的表格还列出了样本中几个单词为垃圾邮件的概率以及正常邮件的概率。

 

有了上面的信息，现在我们来判断新邮件，“review us now”是正常邮件还是垃圾邮件？

 

review us是垃圾邮件的概率，

 

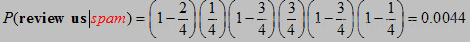
解释如下：password没有在这句出现，所以是（1-2/4）,review出现在这个邮件中，所以是1/4，send也没有出现在这句中，所以是（1-3/4）,后面的也是如此。

 

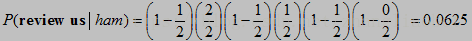
相比之下，是正常邮件的概率高一点。

 

从计算来看，是正常邮件的情况大一点，但是仔细思考一下，review us就多了一个文本中未出现的now，就从垃圾邮件变成了正常邮件。而且由于样本数量较少，我们明显能看到如果邮件中提到“account”，为正常邮件的概率是0，任何包含“account”都是垃圾邮件了。

 

上面的情况就涉及到一个零概率问题。零概率问题就是在计算新实例的概率时，如果某个分量在训练集中从没有出现过，会导致整个实例的概率计算结果为0，这显然是不合理的。为了解决这个问题，引出了拉普拉斯平滑：

朴素贝叶斯中针对属性缺失问题，测试数据中某个可能维度的值丢失，可以不用管，不会受到影响。

5.2.3策略

 

朴素贝叶斯法将实例分到后验概率最大的类中，这等价于期望风险最小化。假设选择0-1损失函数：

 

式中f(X)是分类决策函数。这时，期望风险函数为

 

 为了使期望风险最小化，只需对X=x逐个极小化

 

由此得到：

这样一来，根据期望风险最小化准则就得到了后验概率最大化准则：

5.2.4 高斯判别分析

 

在朴素贝叶斯中，我们假设x是离散的，服从多项分布（包括伯努利分布），在高斯判别分析（Gaussian discriminant analysis，GDA）中，我们假设x是连续的，服从高斯分布。该模型基于两点假设，y服从伯努利分布，特征x是多元高斯分布[2] 。写出分布概率密度为：

同样，我们来比较和的大小：

可以看到GDA实际上是一个线性模型，这是一个判别式模型。

5.3 隐马尔科夫模型

5.3.1模型

 

隐马尔科夫模型（hidden Markov model，HMM）是可用于标注问题的统计学习模型，描述由隐藏的马尔可夫链随机生成观测序列的过程，属于生成模型。隐马尔科夫模型在语音识别、自然语言处理、生物信息、模式识别等领域有着广泛的应用。

（摘自李航统计学习方法）

 

定义：隐马尔科夫模型是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生观测随机序列的过程。隐藏的马尔可夫链随机生成的状态的序列，称为状态序列；每个状态生成一个观测，而由此产生的观测的随机序列，称为观测序列。序列的每一个位置又可以看作是一个时刻。

 

上述定义可能有些抽象，强烈建议大家阅读《数学之美》第五章之后，在来看本节内容，在书中，作者通过生动丰富的例子，非常自然的从马尔科夫过程过渡到隐马尔可夫过程，对于理解上有很大的帮助。

 

隐马尔科夫模型由初始概率分布、状态转移概率分布以及观测概率分布确定。隐马尔科夫模型的形式定义如下：

 

设Q是所有可能的状态的集合，V是所有可能的观测的集合，

其中，N是可能的状态数，M是可能的观测数。

 

隐马尔可夫模型可用三元符号表示，即λ=(A, B, Π)。其中：

 

隐马尔科夫模型由初始状态概率向量π、状态转移概率矩阵A和观测概率矩阵B决定。A,B,π称为隐马尔科夫模型的三要素。

状态转移概率矩阵A与初始状态概率向量π确定了隐藏的隐马尔可夫链，生成不可观测的状态序列，观测概率矩阵B确定了如何从状态生成观测，与状态序列综合确定了如何产生观测序列。

隐马尔科夫模型有三个基本问题：

 

（1）概率计算问题：给定模型λ=(A, B, Π)和观测序列O =（o1,o2,…,oT），计算在模型λ下观测序列O出现的概率P(O|λ)。

 

（2）学习问题：已知观测序列O =（o1,o2,…,oT），估计模型λ=(A, B, Π)参数，使得在该模型下观测序列概率P(O|λ)最大。即用极大似然估计的方法估计参数。

 

（3）预测问题，也称为解码问题。已知模型λ=(A, B, Π)和观测序列O =（o1,o2,…,oT），求对给定观测序列条件概率P(I|O)最大的状态序列I=（i1，i2,...,iT）。即给定观测序列，求最有可能的对应的状态序列。

 

第一个问题对应的算法是前向-后向算法（Forward-Backward algorithm），第二个则是模型训练问题，第三个问题可用维特比算法解决，接下来，我们将逐一介绍。

5.3.2推理（概率计算）

概率计算问题

 

已知：模型λ=(A, B, Π)和观测序列O =（o1,o2,…,oT）

求：P(O|λ)

方法一：直接计算法

通过列举所有可能的长度为T的状态序列I = (i1,i2, ..., iT)，求各个状态序列I与观测序列O = (o1, o2, ..., oT)的联合概率P(O,I|λ)，然后对所有可能的状态序列求和，得到P(O|λ)。

但这个公式计算量很大，算法的复杂度是，类似TNT炸药一样，直接就爆了。那么有什么解决的有效办法吗？

 

下面介绍计算观测序列概率P（O|λ）的有效算法：前向-后向算法。（后向算法下节课会讲到）

 

上面的问题看似非常复杂，其实如果学会一步一步来做，问题也许就会迎刃而解。假设现在我们只有一个观测：

 

■  一个观测

 

表示在第一个时刻（t=1），状态取值为的概率，有N种可能；

 

■  两个观测

表示在第二个时刻（t=2）,状态取值为的概率，有N种可能。

 

■  三个观测

 

相信大家已经发现一些规律，那么我们来总结一下：

 

有了上面的计算公式，我们能够从相应的概率解释直接计算，例如对t=1时刻：

 

---

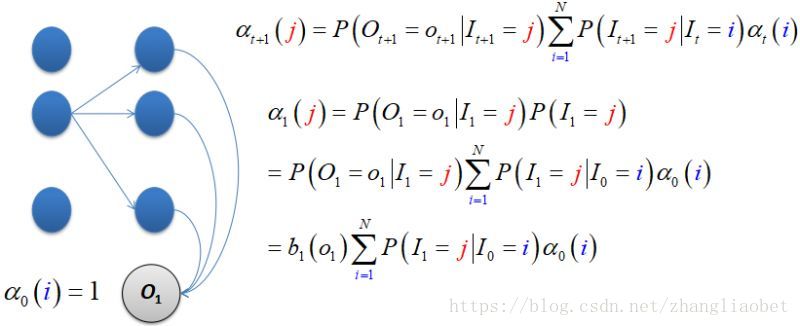
算法(观测序列概率的前向算法)

输入：隐马尔科夫模型λ，观测序列O；

输出：观测序列概率P(O|λ)

---

 

隐马尔可夫模型的其余部分将会在下一讲中继续为大家讲解，感谢阅读~

 

ps：文中所有推导均可在课件中找到，回复「课件」即可领取。

参考文献

[1]https://zhuanlan.zhihu.com/p/23103686

[2]https://blog.youkuaiyun.com/Irving_zhang/article/details/60583862

[3] 李航.统计学习方法.清华大学出版社，北京（2012）

[4] 周志华.机器学习.清华大学出版社,北京（2016）

[5]https://blog.youkuaiyun.com/xueyingxue001/article/details/51435752

[6] Ng, Andrew Y., and Michael I. Jordan. "On discriminative vs. generative classifiers: A comparison of logistic regression and naive bayes." Advances in neural information processing systems. 2002.