计算机图形学：基本变换

于 2020-02-23 13:15:49 发布
阅读量1.5k 收藏 9
点赞数 3
分类专栏： 计算机图形学 文章标签： 线性代数 3d opengl
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/zhanghuanzj/article/details/104458536
版权

基本变换

1 基向量的变换

1.1 基向量的变换

初始基向量为 i ^ ( 1 , 0 ) , j ^ ( 0 , 1 ) \hat{i}(1,0),\hat{j}(0,1) i^(1,0),j^​(0,1),经过变换后变为 i ^ ( 3 , − 2 ) , j ^ ( 2 , 1 ) \hat{i}(3,-2), \hat{j}(2,1) i^(3,−2),j^​(2,1)

image

image

1.2 线性变换对向量的作用

仅需取出向量的坐标，将它们分别于矩阵的特定列相乘，然后将结果相加即可

image

逆时针旋转90°的例子

image

当两个向量变为线性相关时，两个向量共线，二维空间会被挤压到一维

image

2 Transformation Classification(分类)

2.1 Rigid-body Transformation (刚体变换)

物体本身的长度、角度、大小不会变化包括：

  • Identity（不变）
  • Translation（平移）
  • Rotation（旋转）
  • 以及他们的组合

image

2.2 Similarity Transformation(相似变换)

保持角度

  • Identity（不变）
  • Translation（平移）
  • Rotation（旋转）
  • Isotropic Scaling（均衡缩放）
  • 以及他们的组合

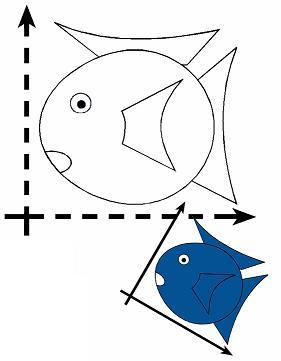
image

2.3 Linear Transformation(线性变换)

线性变换满足如下方程：

L(p + q) = L(p) + L(q)

aL(p) = L(ap)
  • Identity（不变）
  • Rotation（旋转）
  • Scaling（缩放）
  • Reflection(对称)
  • Shear(切变、剪切)

image

2.4 Affine Transformation(仿射变换)

保持直线以及直线与直线的平行

  • 线性变换
  • 相似变换
  • 以及它们的组合

image

2.5 Projective Transformation(投影变换)

image

  • Grid lines remain parallel and evenly spaced and such that the origin remains fixed.
  • 它保持网格线平行且等距分布，并且保持原点不动

3 Homogeneous Coordinates(齐次坐标)

  • The objective of HC is to use a 4D column matrices to represent both points and vectors in 3D
  • 齐次坐标的本质是使用四维数组来表示三维空间中的点和向量
  • If we multiply a homogeneous coordinate by an affine matrix, w is unchanged; by an projective matrix, the value of w will change
  • w=0时齐次坐标表示一个方向而不是一个点

3.1 Translate

[ x ′ y ′ z ′ 1 ] = [ 1 0 0 t x 0 1 0 t y 0 0 1 t z 0 0 0 1 ] ⋅ [ x y z 1 ] \begin{bmatrix} x'\\ y'\\ z' \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & t_x\\ 0 & 1 & 0 & t_y\\ 0 & 0 & 1 & t_z\\ 0 & 0 & 0 & 1 \end{bmatrix}\cdot \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} ⎣⎢⎢⎡​x′y′z′1​⎦⎥⎥⎤​=⎣⎢⎢⎡​1000​0100​0010​tx​ty​tz​1​⎦⎥⎥⎤​⋅⎣⎢⎢⎡​xyz1​⎦⎥⎥⎤​

3.2 Scale

P ′ = [ a 0 0 0 b 0 0 0 a ] ⋅ [ P x P y P z ] P' = \begin{bmatrix} a & 0 & 0\\ 0 & b & 0\\ 0 & 0 & a \end{bmatrix}\cdot \begin{bmatrix} P_x\\ P_y\\ P_z \end{bmatrix} P′=⎣⎡​a00​0b0​00a​⎦⎤​⋅⎣⎡​Px​Py​Pz​​⎦⎤​

image

3.3 Rotation

取[-y, x]为Q作为垂直于P的向量，则：

P ′ = P c o s θ + Q s i n θ P' = Pcos\theta + Q sin\theta P′=Pcosθ+Qsinθ
{ P x ′ = P x c o s θ − P y s i n θ P y ′ = P y c o s θ + P x s i n θ \left\{\begin{matrix} P_x' = P_xcos\theta - P_ysin\theta\\ P_y' = P_ycos\theta + P_xsin\theta \end{matrix}\right. {Px′​=Px​cosθ−Py​sinθPy′​=Py​cosθ+Px​sinθ​
P ′ = [ c o s θ − s i n θ s i n θ c o s θ ] P P' = \begin{bmatrix} cos\theta & -sin\theta\\ sin\theta & cos\theta\\ \end{bmatrix}P P′=[cosθsinθ​−sinθcosθ​]P

image

image

R z ( θ ) = [ c o s θ − s i n θ 0 s i n θ c o s θ 0 0 0 1 ] R_z(\theta) = \begin{bmatrix} cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0 & 0 & 1\\ \end{bmatrix} Rz​(θ)=⎣⎡​cosθsinθ0​−sinθcosθ0​001​⎦⎤​
R x ( θ ) = [ 1 0 0 0 c o s θ − s i n θ 0 s i n θ c o s θ ] R_x(\theta) = \begin{bmatrix} 1 & 0 & 0\\ 0 & cos\theta & -sin\theta\\ 0 & sin\theta & cos\theta\\ \end{bmatrix} Rx​(θ)=⎣⎡​100​0cosθsinθ​0−sinθcosθ​⎦⎤​
R y ( θ ) = [ c o s θ 0 s i n θ 0 1 0 − s i n θ 0 c o s θ ] R_y(\theta) = \begin{bmatrix} cos\theta & 0 & sin\theta\\ 0 & 1 & 0\\ -sin\theta & 0 & cos\theta\\ \end{bmatrix} Ry​(θ)=⎣⎡​cosθ0−sinθ​010​sinθ0cosθ​⎦⎤​

3.4 Rotation About an Arbitrary Axis

p r o j A P = ( A ⋅ P ) A p e r p A P = P − ( A ⋅ P ) A proj_AP = (A\cdot P)A\\ perp_AP = P - (A\cdot P)A projA​P=(A⋅P)AperpA​P=P−(A⋅P)A

因为与A重合的旋转后不会改变，所以仅需计算垂直的向量即可。为了计算 p e r p A P perp_AP perpA​P的旋转，需要先得到与其垂直的向量，即 A × P A\times P A×P

rotation of p e r p A P perp_AP perpA​P through an angle θ as
P ′ = [ P − ( A ⋅ P ) A ] c o s θ + ( A × P ) s i n θ + ( A ⋅ P ) A P' = [P - (A\cdot P)A]cos\theta + (A \times P)sin\theta + (A\cdot P)A P′=[P−(A⋅P)A]cosθ+(A×P)sinθ+(A⋅P)A
image

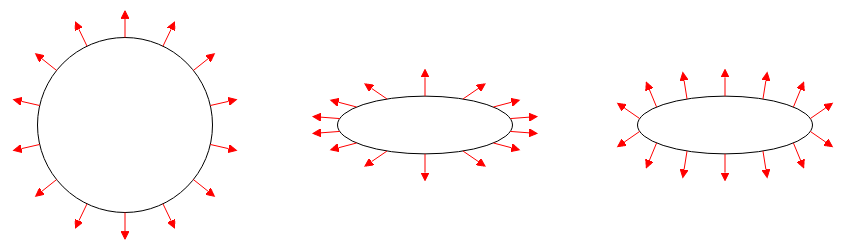
3.5 Transforming Normal Vectors

We could find that translation, rotation and isotropic scale preserve the correct normal, but shear or isotropic scale will make the normal incorrect.
在这里插入图片描述

If M is a 3×3 matrix with which we transform a vertex position, then the same matrix M
can be used to correctly transform the tangent vector at that vertex.

N , T N,T N,T为变换前的法向量和切向量， N ′ , T ′ N',T' N′,T′为变换后的法向量和切向量，则：

N ⋅ T = N T T = 0 N\cdot T = N^T T = 0 N⋅T=NTT=0
N ′ ⋅ T ′ = N ′ T T ′ = 0 N'\cdot T' = N'^T T' = 0 N′⋅T′=N′TT′=0
N T ( M − 1 M ) T = N T M − 1 T ′ = 0 N^T (M^{-1} M)T = N^TM^{-1} T'= 0 NT(M−1M)T=NTM−1T′=0
N ′ T = N T M − 1 N'^T = N^TM^{-1} N′T=NTM−1
N ′ = ( M − 1 ) T N N' = (M^{-1})^T N N′=(M−1)TN

So the matrix is the transpose of inverse of M

4 Projection

image

大拇指指向为x轴正方向，食指指向为y轴正方向，中指指向为z轴正方向，OpenGL采用右手坐标系，DirectX为左手坐标系

4.1 Orthographic Projection(正交投影)

When the focal point is at infinity, the rays are parallel and orthogonal to the image plane, When xy-plane is the image plane, ( x , y , z ) − > ( x , y , 0 ) \bm{(x,y,z) -> (x,y,0)} (x,y,z)−>(x,y,0)

image

4.2 正交投影矩阵

image

为了后续裁剪的方便，我们需要将物体的坐标转换到canonical view volume (CVV) 中，转换后的坐标被称为normalized device coordinates (NDC)，这里l，r，b，t，n，f采用对应的x轴y轴z轴坐标值。投影就是将长方形的视域体压缩到指定范围即可，从x轴开始，视域体中的点的x坐标范围在[l, r]，想把它变换到范围在[-1, 1]：

l ⩽ x ⩽ r 0 ⩽ x − l ⩽ r − l 0 ⩽ x − l r − l ⩽ 1 − 1 ⩽ 2 ( x − l ) r − l − 1 ⩽ 1 − 1 ⩽ 2 x r − l − r + l r − l ⩽ 1 x ′ = 2 r − l x − r + l r − l l\leqslant x \leqslant r \\ 0\leqslant x - l \leqslant r - l \\ 0\leqslant \frac{x - l}{r - l} \leqslant 1 \\ -1\leqslant \frac{2(x - l)}{r - l} - 1 \leqslant 1 \\ -1\leqslant \frac{2x}{r - l} - \frac{r + l}{r - l} \leqslant 1 \\ x' = \frac{2}{r - l}x - \frac{r + l}{r - l} l⩽x⩽r0⩽x−l⩽r−l0⩽r−lx−l​⩽1−1⩽r−l2(x−l)​−1⩽1−1⩽r−l2x​−r−lr+l​⩽1x′=r−l2​x−r−lr+l​

y同理
y ′ = 2 t − b y − t + b t − b y' = \frac{2}{t - b}y - \frac{t + b}{t - b} y′=t−b2​y−t−bt+b​

z需要在z=n时映射为-1，z=f时映射为1
− 1 = n A + B 1 = f A + B A = 2 f − n B = − f + n f − n -1 = nA + B \\ 1 = fA + B \\ A = \frac{2}{f - n} \\ B = -\frac{f + n}{f - n} \\ −1=nA+B1=fA+BA=f−n2​B=−f−nf+n​

所以z’为

z ′ = 2 f − n z − f + n f − n z' = \frac{2}{f - n}z - \frac{f + n}{f - n} z′=f−n2​z−f−nf+n​

所以正交投影矩阵为

[ 2 r − l 0 0 − r + l r − l 0 2 t − b 0 − t + b t − b 0 0 2 f − n − f + n f − n 0 0 0 1 ] \begin{bmatrix} \frac{2}{r - l} & 0 & 0 & -\frac{r + l}{r - l}\\ 0 & \frac{2}{t - b} & 0 & -\frac{t + b}{t - b}\\ 0 & 0 & \frac{2}{f - n} & -\frac{f + n}{f - n}\\ 0 & 0 & 0 & 1 \end{bmatrix} ⎣⎢⎢⎡​r−l2​000​0t−b2​00​00f−n2​0​−r−lr+l​−t−bt+b​−f−nf+n​1​⎦⎥⎥⎤​

通常情况下摄像机定位在原点并且沿着z轴方向观看，所以l与r，b与t是轴对称的，我们可以定义宽度为w = r - l，高度为h = t - b，矩阵可以简化为

[ 2 w 0 0 0 0 2 h 0 0 0 0 2 f − n − f + n f − n 0 0 0 1 ] \begin{bmatrix} \frac{2}{w} & 0 & 0 & 0\\ 0 & \frac{2}{h} & 0 & 0\\ 0 & 0 & \frac{2}{f - n} & -\frac{f + n}{f - n}\\ 0 & 0 & 0 & 1 \end{bmatrix} ⎣⎢⎢⎡​w2​000​0h2​00​00f−n2​0​00−f−nf+n​1​⎦⎥⎥⎤​

4.2.1 OpenGL正交投影矩阵

在OpenGL中n，f为正值，表示距离相机的远近，所以要对投影矩阵中的n,f取负

[ 2 r − l 0 0 − r + l r − l 0 2 t − b 0 − t + b t − b 0 0 − 2 f − n − f + n f − n 0 0 0 1 ] \begin{bmatrix} \frac{2}{r - l} & 0 & 0 & -\frac{r + l}{r - l}\\ 0 & \frac{2}{t - b} & 0 & -\frac{t + b}{t - b}\\ 0 & 0 & -\frac{2}{f - n} & -\frac{f + n}{f - n}\\ 0 & 0 & 0 & 1 \end{bmatrix} ⎣⎢⎢⎡​r−l2​000​0t−b2​00​00−f−n2​0​−r−lr+l​−t−bt+b​−f−nf+n​1​⎦⎥⎥⎤​

4.2.2 DirectX正交投影矩阵

DirectX坐标轴z轴朝里，且将z值映射为[0,1]所以，DirectX的正交投影矩阵为

[ 2 r − l 0 0 − r + l r − l 0 2 t − b 0 − t + b t − b 0 0 1 f − n − n f − n 0 0 0 1 ] \begin{bmatrix} \frac{2}{r - l} & 0 & 0 & -\frac{r + l}{r - l}\\ 0 & \frac{2}{t - b} & 0 & -\frac{t + b}{t - b}\\ 0 & 0 & \frac{1}{f - n} & -\frac{n}{f - n}\\ 0 & 0 & 0 & 1 \end{bmatrix} ⎣⎢⎢⎡​r−l2​000​0t−b2​00​00f−n1​0​−r−lr+l​−t−bt+b​−f−nn​1​⎦⎥⎥⎤​

4.3 Perspective Projection(透视投影)

image

When
  • The camera is at the origin point and looks along the z-axis
  • The image plane is paraellel to the xy-plane at distance d
  • ( x , y , z ) − > ( ( − d / z ) x , ( − d / z ) y , d ) \bm{(x,y,z) -> ((-d/z)x, (-d/z)y, d)} (x,y,z)−>((−d/z)x,(−d/z)y,d)

4.4 透视投影矩阵

image

4.4.1 透视投影矩阵

在透视投影中将点投影的近平面，则x与y的变化如下

x ′ = n z x y ′ = n z y x' = \frac{n}{z}x \\ y' = \frac{n}{z}y \\ x′=zn​xy′=zn​y

然后用正交投影的公式，就可以把x和y的坐标转换到[-1, 1]的范围内

x ′ = 2 r − l n z x − r + l r − l y ′ = 2 t − b n z y − t + b t − b x' = \frac{2}{r - l}\frac{n}{z}x - \frac{r + l}{r - l} \\ y' = \frac{2}{t - b}\frac{n}{z}y - \frac{t + b}{t - b}\\ x′=r−l2​zn​x−r−lr+l​y′=t−b2​zn​y−t−bt+b​

这里有个z，无法直接用矩阵表示，我们可以两边都乘以z

x ′ z = 2 n r − l x − r + l r − l z y ′ z = 2 n t − b y − t + b t − b z x'z = \frac{2n}{r - l}x - \frac{r + l}{r - l}z \\ y'z = \frac{2n}{t - b}y - \frac{t + b}{t - b}z\\ x′z=r−l2n​x−r−lr+l​zy′z=t−b2n​y−t−bt+b​z

对于变换后的z’来说，z’并不依赖于x和y，为了统一我们也将z’乘以z，因此z’z = az + b，z=-n时，z’=-1；z=-f时，z’=1，于是z’z如下

z ′ z = f + n f − n z − 2 f n f − n z'z = \frac{f + n}{f - n}z - \frac{2fn}{f - n} z′z=f−nf+n​z−f−n2fn​

最终透视投影矩阵如下

[ 2 n r − l 0 − r + l r − l 0 0 2 n t − b − t + b t − b 0 0 0 f + n f − n − 2 f n f − n 0 0 1 0 ] \begin{bmatrix} \frac{2n}{r - l} & 0 & -\frac{r + l}{r - l} & 0\\ 0 & \frac{2n}{t - b} & -\frac{t + b}{t - b} & 0\\ 0 & 0 & \frac{f + n}{f - n} & - \frac{2fn}{f - n}\\ 0 & 0 & 1 & 0 \end{bmatrix} ⎣⎢⎢⎡​r−l2n​000​0t−b2n​00​−r−lr+l​−t−bt+b​f−nf+n​1​00−f−n2fn​0​⎦⎥⎥⎤​

通过矩阵计算得到的结果是(x’z, y’z, z’z, z)。可以看出，w分量此时等于变换之前的z，然后，你应用通常的步骤去除以齐次坐标，得到(x’, y’, z’, 1)

4.4.2 OpenGL透视投影矩阵

在OpenGL中n，f为正值，表示距离相机的远近，所以要对投影矩阵中的n,f取负

x ′ = − n z x y ′ = − n z y x' = \frac{-n}{z}x \\ y' = \frac{-n}{z}y\\ x′=z−n​xy′=z−n​y
这里有个-z，无法直接用矩阵表示，我们可以两边都乘以-z

− x ′ z = 2 n r − l x + r + l r − l z − y ′ z = 2 n t − b y + t + b t − b z − z ′ z = − f + n f − n z − 2 f n f − n -x'z = \frac{2n}{r - l}x + \frac{r + l}{r - l}z \\ -y'z = \frac{2n}{t - b}y + \frac{t + b}{t - b}z \\ -z'z = -\frac{f + n}{f - n}z - \frac{2fn}{f - n} \\ −x′z=r−l2n​x+r−lr+l​z−y′z=t−b2n​y+t−bt+b​z−z′z=−f−nf+n​z−f−n2fn​

最终OpenGL透视投影的矩阵如下

[ 2 n r − l 0 r + l r − l 0 0 2 n t − b t + b t − b 0 0 0 − f + n f − n − 2 f n f − n 0 0 − 1 0 ] \begin{bmatrix} \frac{2n}{r - l} & 0 & \frac{r + l}{r - l} & 0\\ 0 & \frac{2n}{t - b} & \frac{t + b}{t - b} & 0\\ 0 & 0 & -\frac{f + n}{f - n} & - \frac{2fn}{f - n}\\ 0 & 0 & -1 & 0 \end{bmatrix} ⎣⎢⎢⎡​r−l2n​000​0t−b2n​00​r−lr+l​t−bt+b​−f−nf+n​−1​00−f−n2fn​0​⎦⎥⎥⎤​

4.4.2 DirectX透视投影矩阵

DirectX坐标轴z轴朝里，且将z值映射为[0,1]，因此z’z = az + b，z=n时，z’=0；z=f时，z’=1，于是z’z如下

z ′ z = f f − n z − f n f − n z'z = \frac{f}{f - n}z - \frac{fn}{f - n} z′z=f−nf​z−f−nfn​

最终DirectX透视投影的矩阵如下
[ 2 n r − l 0 − r + l r − l 0 0 2 n t − b − t + b t − b 0 0 0 f f − n − f n f − n 0 0 1 0 ] \begin{bmatrix} \frac{2n}{r - l} & 0 & -\frac{r + l}{r - l} & 0\\ 0 & \frac{2n}{t - b} & -\frac{t + b}{t - b} & 0\\ 0 & 0 & \frac{f}{f - n} & - \frac{fn}{f - n}\\ 0 & 0 & 1 & 0 \end{bmatrix} ⎣⎢⎢⎡​r−l2n​000​0t−b2n​00​−r−lr+l​−t−bt+b​f−nf​1​00−f−nfn​0​⎦⎥⎥⎤​

4.4.3 以FOV表示的透视投影矩阵

image

2 n t − b = n h 2 = c o t f o v 2 2 n r − l = 2 n w = n h 2 1 a s p e c t = c o t f o v 2 1 a s p e c t a s p e c t = w h \frac{2n}{t - b} = \frac{n}{\frac{h}{2}} = cot\frac{fov}{2}\\ \frac{2n}{r - l} = \frac{2n}{w} = \frac{n}{\frac{h}{2}} \frac{1}{aspect} = cot\frac{fov}{2}\frac{1}{aspect}\\ aspect = \frac{w}{h}\\ t−b2n​=2h​n​=cot2fov​r−l2n​=w2n​=2h​n​aspect1​=cot2fov​aspect1​aspect=hw​

所以矩阵可以表示为

[ c o t f o v 2 a s p e c t 0 0 0 0 c o t f o v 2 0 0 0 0 f + n f − n − 2 f n f − n 0 0 1 0 ] \begin{bmatrix} \frac{cot\frac{fov}{2}}{aspect} & 0 & 0 & 0\\ 0 & cot\frac{fov}{2} & 0 & 0\\ 0 & 0 & \frac{f + n}{f - n} & - \frac{2fn}{f - n}\\ 0 & 0 & 1 & 0 \end{bmatrix} ⎣⎢⎢⎢⎡​aspectcot2fov​​000​0cot2fov​00​00f−nf+n​1​00−f−n2fn​0​⎦⎥⎥⎥⎤​

5 屏幕映射

屏幕映射主要是将裁剪空间内的坐标映射成屏幕坐标，以显示到屏幕上。

image

image

x将从 [ − 1 , 1 ] [-1, 1] [−1,1]映射到 [ x 1 , x 2 ] [x_1, x_2] [x1​,x2​]

{ − A + B = x 1 A + B = x 2 x ′ = x 2 − x 1 2 x + x 1 + x 2 2 \left\{\begin{matrix} -A + B = x_1\\ A + B = x_2 \end{matrix}\right. \\ x' = \frac{x_2 - x_1}{2}x + \frac{x_1 + x_2}{2} {−A+B=x1​A+B=x2​​x′=2x2​−x1​​x+2x1​+x2​​

同理y’
y ′ = y 2 − y 1 2 y + y 1 + y 2 2 y' = \frac{y_2 - y_1}{2}y + \frac{y_1 + y_2}{2} y′=2y2​−y1​​y+2y1​+y2​​

5.1 OpenGL屏幕映射

在OpenGL中 x 1 = 0 , x 2 = w , y 1 = 0 , y 2 = h x_1 = 0, x_2 = w, y_1 = 0, y_2 = h x1​=0,x2​=w,y1​=0,y2​=h，所以映射矩阵为

[ w 2 0 0 w 2 0 h 2 0 h 2 0 0 1 0 0 0 0 1 ] \begin{bmatrix} \frac{w}{2} & 0 & 0 & \frac{w}{2}\\ 0 & \frac{h}{2} & 0 & \frac{h}{2}\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} ⎣⎢⎢⎡​2w​000​02h​00​0010​2w​2h​01​⎦⎥⎥⎤​

5.2 DirectX屏幕映射

在DirectX中 x 1 = 0 , x 2 = w , y 1 = h , y 2 = 0 x_1 = 0, x_2 = w, y_1 = h, y_2 = 0 x1​=0,x2​=w,y1​=h,y2​=0，所以映射矩阵为

[ w 2 0 0 w 2 0 − h 2 0 h 2 0 0 1 0 0 0 0 1 ] \begin{bmatrix} \frac{w}{2} & 0 & 0 & \frac{w}{2}\\ 0 & -\frac{h}{2} & 0 & \frac{h}{2}\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} ⎣⎢⎢⎡​2w​000​0−2h​00​0010​2w​2h​01​⎦⎥⎥⎤​

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值