快速排序（未优化）

实现原理：通过一趟排序将待排序记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，则可以分别对这两部分记录进行排序，以达到整个序列有序的目的。

时间复杂度：最坏情况下待排序的序列正序或者逆序，此时需要执行n-1次递归调用，且第i次划分需要经过n-i次的比较才能找到第i个记录，比较次数为（n*(n-1))/2。时间复杂度为O(n^2)。最好的情况下，时间复杂度为O(nlogn)。总而言之，平均时间复杂度为O(nlogn)。

空间复杂度：主要是递归造成的栈空间的使用。最好的情况下，空间复杂度为O(logn)。最坏情况下，空间复杂度为O(n)。平均空间复杂度为O(logn)。

代码实现：

#include <stdio.h>
#include <stdlib.h>

void swap(int *a,int *b){
    int temp = *a;
    *a = *b;
    *b = temp;
}
int count = 0;
void QuickSort(int arr[], int l, int h){

    if(l >= h)
        return;
    int i = l;
    int j = h;
    int temp = arr[l];
    while(i < j){
        while(i<j && arr[j] >= temp) j--;
        while(i<j && arr[i] <= temp) i++;
        swap(&arr[i],&arr[j]);
    }
    swap(&arr[l],&arr[i]);
    printf("第%d结果为:",++count);
    int k;
    for(k=0; k<=11; k++){
        printf("%d ",arr[k]);
        if(k==11){
            printf("\n");
       }
    }
    QuickSort(arr,l,i);
    QuickSort(arr,i+1,h);
}
int main()
{
    int arr[] = {10,56,78,2,34,21,11,43,67,90,33};
    printf("待排序序列为:");
    int k;
    for(k=0; k<=11; k++){
        printf("%d ",arr[k]);
        if(k==11){
            printf("\n");
       }
    }
    QuickSort(arr,0,11);
    return 0;
}

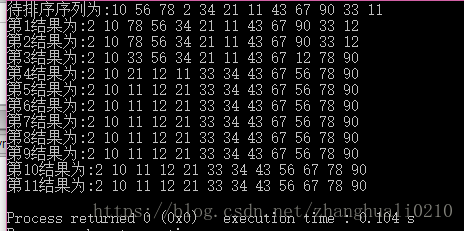
实验结果：