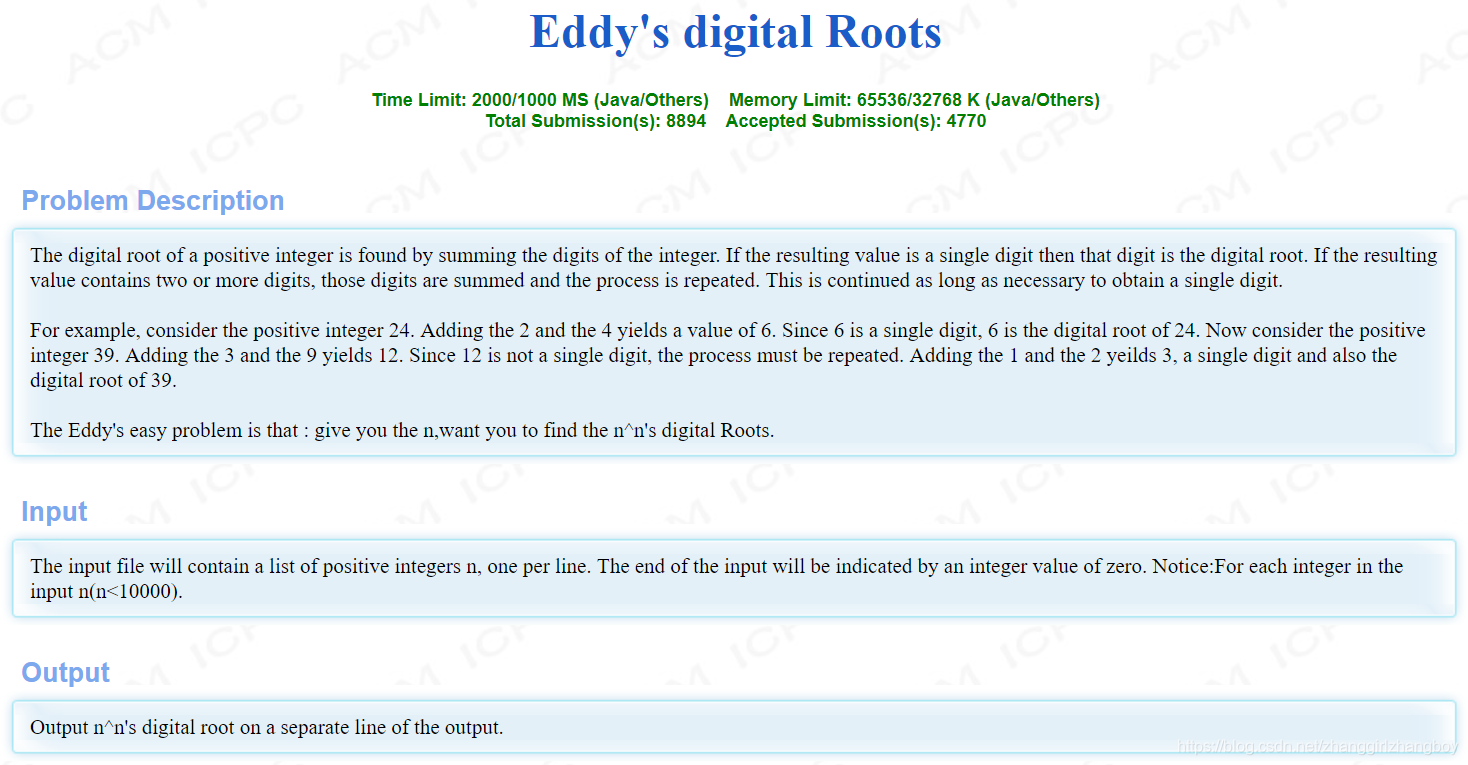
注解
1、数位求和。
2、九余数定理:一个数a各位数字的和,对9取余等于这个数对9取余。
3、字根a,然后求 a * n的原根,赋给 a,接着依次求 a * n,求 n-1 次,就得到了 n^n 的数字根。
代码
#include <iostream>
using namespace std;
int main() {
int n;
cin>>n;
while(n) {
int temp = n;
for(int i=1; i<n; i++) {
temp = temp * n % 9;
}
int ans = temp==0?9:temp;
cout<<ans<<endl;
cin>>n;
}
return 0;
}
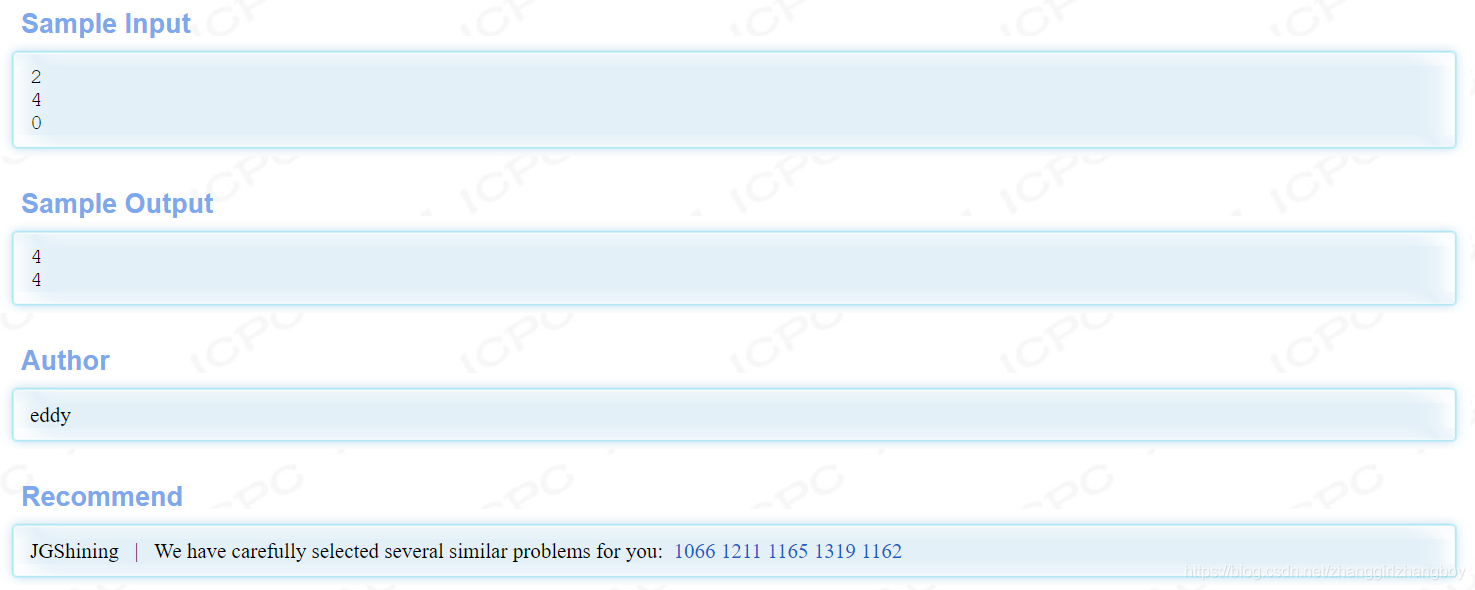
结果






 本文探讨了九余数定理在数位求和问题中的应用,介绍了一个快速计算n^n数字根的算法。通过将n^n的操作简化为对9取余,避免了大数运算,提高了效率。
本文探讨了九余数定理在数位求和问题中的应用,介绍了一个快速计算n^n数字根的算法。通过将n^n的操作简化为对9取余,避免了大数运算,提高了效率。
















 3415
3415

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








