拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush-Kuhn-Tucker)条件是求解约束优化问题的重要方法,在有等式约束时使用拉格朗日乘子法,在有不等约束时使用KKT条件。前提是:只有当目标函数为凸函数时,使用这两种方法才保证求得的是最优解。
对于无约束最优化问题,有很多经典的求解方法,参见无约束最优化方法。
拉格朗日乘子法

转换为

系数λi称为拉格朗日乘子。
下面看一下wikipedia上是如何解释拉格朗日乘子法的合理性的。
现有一个二维的优化问题:

我们可以画图来辅助思考。

绿线标出的是约束g(x,y) = c的点的轨迹。蓝线是f的等高线。箭头表示斜率,和等高线的法线平行。
从图上可以直观地看到在最优解处,f和g的斜率平行。
 λ ≠ 0
λ ≠ 0
一旦求出λ的值,将其套入下式,易求在无约束极值和极值所对应的点。
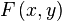 =
= 
新方程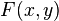 在达到极值时与
在达到极值时与 相等,因为
相等,因为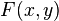 达到极值时
达到极值时 总等于零。
总等于零。
KKT条件
对于带约束优化问题

KKT条件指出,在最优解处X*应该满足:






 本文详细介绍了拉格朗日乘子法及KKT条件在约束优化问题中的应用,强调了这两种方法适用于不同类型的约束条件,并指出在目标函数为凸函数时能保证求得最优解。
本文详细介绍了拉格朗日乘子法及KKT条件在约束优化问题中的应用,强调了这两种方法适用于不同类型的约束条件,并指出在目标函数为凸函数时能保证求得最优解。
















 7640
7640

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








